节选自：https://mp.weixin.qq.com/s/1byx-MPeT0IfrBKwHFsZLg

二叉树前中后序遍历

前序遍历题目如下：
root节点是A节点，然后按照下图数字顺序依次打印节点：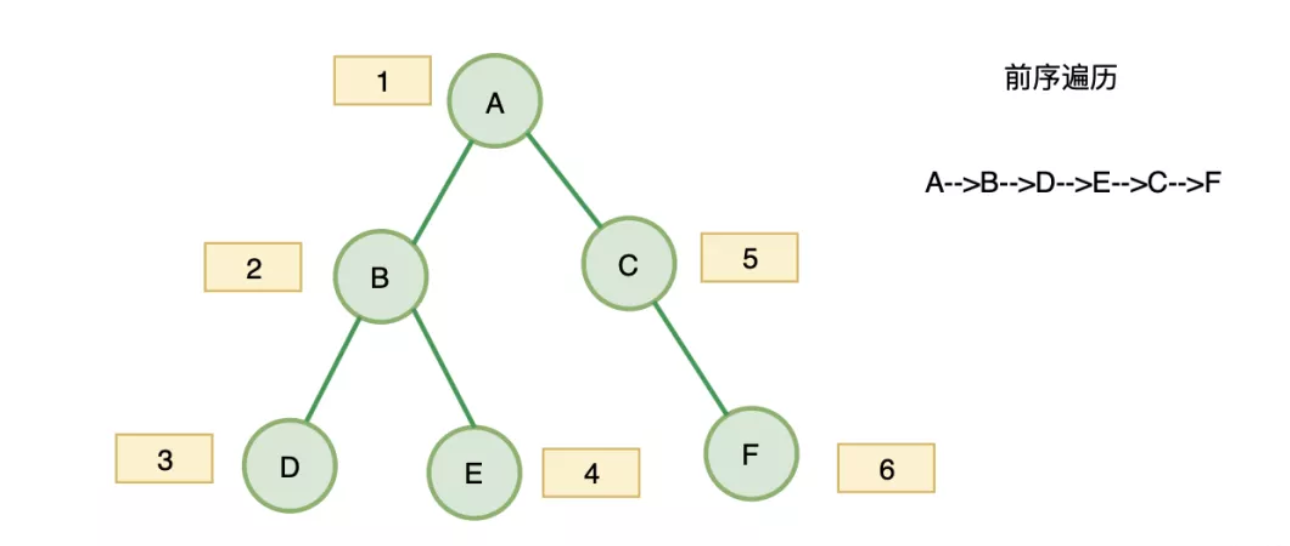
image.png
从这里可以看到，是 深度优先遍历，先遍历左子树，再遍历右子树 。
如果使用递归的方式，将会是

  1. /**
  2.  * Definition for a binary tree node.
  3.  * function TreeNode(val, left, right) {
  4.  *     this.val = (val===undefined ? 0 : val)
  5.  *     this.left = (left===undefined ? null : left)
  6.  *     this.right = (right===undefined ? null : right)
  7.  * }
  8.  *
  9. **/
  11. function preorderTraversal (root) {
  12.     const arr = [] // 作为外部变量，存储结果
  13.   function preorder (root, arr) {
  14.       if (!root || !root.val) return []
  15.     arr.push(root.val)
  16.     // 递归调用root.left, root.right。 
  17.     // 无需判断root.left 存在与否，因为上面已经做了异常判定
  18.     preorder(root.left, arr)
  19.     preorder(root.right, arr)
  20.   }
  21.     preorder(root, arr)
  22.   return arr
  23. }

首先要明白什么事二叉树的前序遍历：
根节点 -> 左节点 -> 右节点 的方式遍历这棵树，而在访问左子树或右子树的时候，按照同样的方式遍历，直至遍历完成。因此整个遍历过程天然具有递归的性质。 :::info 前序遍历： 根节点 -> 左子树 -> 右子树
中序遍历： 左子树 -> 根节点 -> 右子树
后序遍历：左子树 -> 右子树 -> 根节点
层级遍历: 只需要按层级遍历即可 :::

一些大厂会要求不使用递归，那么我们需要一套如何遍历一颗二叉树，并且先左子树，后右子树的通用模板。


前序遍历

通用模板

  1. // 迭代法
  2. function traversal (root) {
  3.   const res = []
  4.     const stack = [] // 维护一个栈，记录按顺序进入的节点
  5.   while (root || stack.length) { // 只要栈不为空，就继续执行
  6.       while(root) { // 只要节点不为空，就继续执行
  7.       res.push(root.val) // 存储遍历的值
  8.         stack.push(root) // 入栈
  9.       root = root.left // 左侧的节点也要不断经历入栈的过程。赋值后继续执行while
  10.     }
  11.     // 执行到这里，说明上一个while里的root为false了，即最左边的一条线上的节点已经入栈完毕了
  12.     // 这时候将最后一个入栈的节点拿出来，看它的右子节点的情况
  13.     root = stack.pop()
  14.     // 右子节点也会经历同样的过程
  15.     root = root.right
  16.   }
  17.   return res
  18. }

结合图片分析，整个入栈过程是

  • A B D 入栈
  • D出栈
  • B出栈
  • E入栈
  • E出栈
  • A出栈
  • C入栈
  • C出栈
  • F入栈
  • F出栈

这里面的元素按入栈顺序排列，就是A -> B -> D -> E -> C -> F, 即前序遍历顺序。

中序遍历

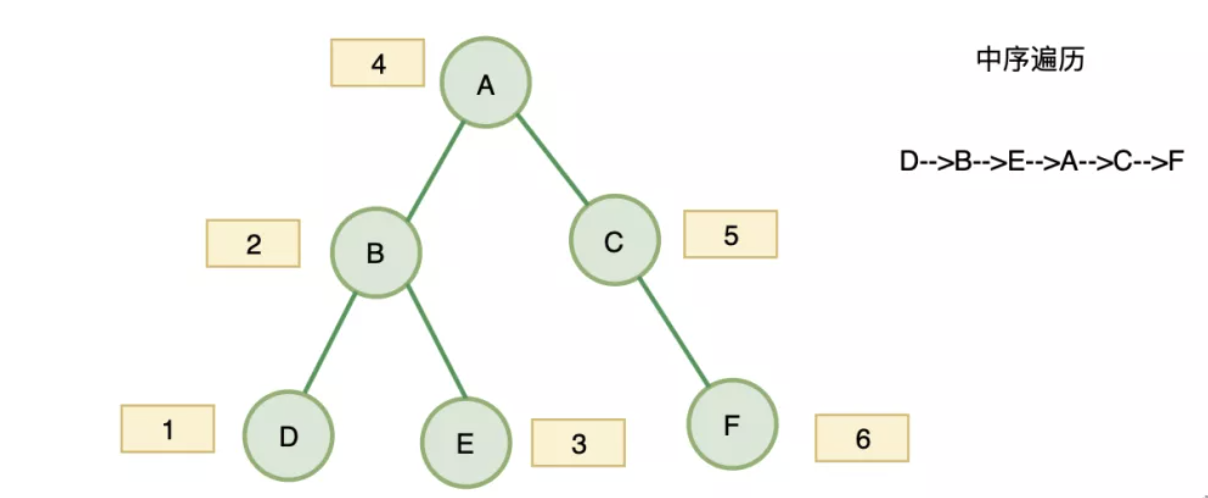
image.png
中序遍历的递归法

  1. // 中序遍历，每个节点内都是按照 左 -> 中 -> 右 的顺序
  2. var inorderTraversal = function(root) {
  3.   const res = []
  4.   function temp (root) {
  5.     if (root && root.left) temp(root.left) // 递归调用，只要是root.left存在，就会一直往左边走，一直做到左边没有了，才会进入下一行
  6.     if (root && root.val) res.push(root.val)
  7.     if (root && root.right) temp(root.right)
  8.   }
  9.   temp(root)
  10.   return res
  11. };

通用模板

  1. function preorderTraversal (root) {
  2.     const stack = []
  3.   const res = []
  4.   while (root || stack.length) {
  5.       while (root) {
  6.       stack.push(root)
  7.       root = root.left
  8.     }
  9.     res.push(root.val)
  10.     root = stack.pop()
  11.     root = root.right
  12.   }
  13.     return res
  14. }

遍历的入栈出栈顺序是一致的，还是按照从上到下，从左到右的顺序入栈，只不过在记录的时候，记录出栈的顺序。出栈顺序就是中序遍历。

后序遍历

后序遍历 左子树 -> 右子树 -> 根节点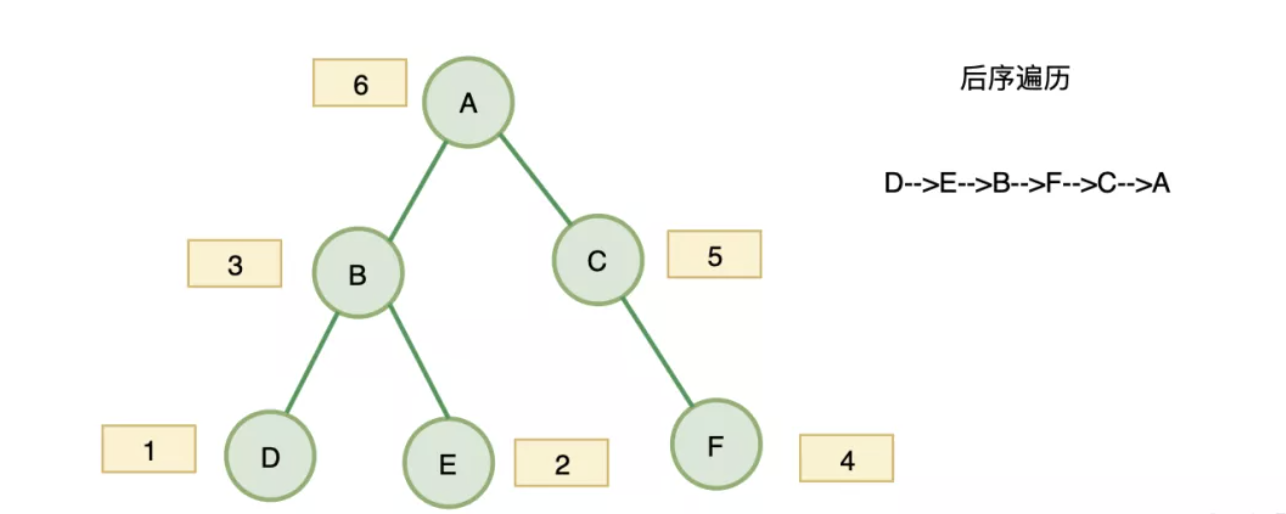
image.png
后序遍历递归调用法

  1. /**
  2.  * @param {TreeNode} root
  3.  * @return {number[]}
  4.  */
  5. // 后序遍历： 左 -> 右 -> 中
  6. var postorderTraversal = function(root) {
  7.   const res = []
  8.   function temp(root) {
  9.     if (root && root.left) temp(root.left)
  10.     if (root && root.right) temp(root.right)
  11.     if (root && root.val) res.push(root.val)
  12.   }
  13.   temp(root)
  14.   return res
  15. };

通用模板

  1. function preorderTraversal (root) {
  2.     const stack = []
  3.   const res = []
  4.   while (root || stack.length) {
  5.       while(root) {
  6.       res.push(root.val) // 或者 res.unshift(root.val) 插入第一位
  7.         stack.push(root)
  8.       root = root.right
  9.     }
  10.     root = stack.pop()
  11.     root = root.left
  12.   }
  13.   return res.reverse()
  14. }
  16. // 这里后序遍历，左 -> 右 -> 中，其实可以看成是 中 -> 右 -> 左的倒序。
  17. // 那么我们在遍历的时候，按照先右后左的顺序，只不过每次遍历的节点值，插在后面
  18. var postorderTraversal = function(root) {
  19.   const res = []
  20.   const stack = []
  21.   while(root || stack.length) {
  22.     while(root) {
  23.       stack.push(root)
  24.       res.unshift(root.val) // 插在队尾
  25.       root = root.right
  26.     }
  27.     root = stack.pop()
  28.     root = root.left
  29.   }
  30.   return res
  31. }
  33. // 或者这种解法也是这个思路
  34. const postorderTraversal = root => {
  35.     if (!root) return [];
  36.     const arr = [root];
  37.     const res = [];
  38.     while (arr.length) {
  39.         const n = arr.pop();
  40.         res.unshift(n.val); // 插入队尾
  41.         n.left && arr.push(n.left);
  42.         n.right && arr.push(n.right); // 那每次就先pop出来right
  43.     }
  44.     return res;
  45. };

后序遍历和前序遍历的区别就在于，先入栈的元素，放在后面。从图中 654321的顺序可以观察出来，其实就是从右向左的遍历过程。

总结：
从三种递归调用的方法中可以看出，递归都是在调用 temp(root.left) 和 temp(root.right), 无非是res.push(root.val)的时机不同而已。
通过前中后序遍历二叉树可以看出，无论哪种顺序，二叉树都是从上到下进行遍历的，无非是是记录入栈的顺序还是出栈的顺序，从先左边还是先右边而已， 没有魔法。

对称二叉树

待续
判断一棵树是否是对称的，例如 二叉树 [1,2,2,3,4,4,3] 是对称的
1
/ \
2 2
/ \ / \
3 4 4 3
但是 [1,2,2,null,3, null,3] 就不是对称的
1
/ \
2 2
\ \
3 3

思路：递归解决

  • 判断两个指针当前节点值是否相等
  • 判断A的右子树与B的左子树是否对称
  • 判断A的左子树和B的右子树是否对称

关键在于找到一个合适的递归时机

  1. /**
  2.  * @param {TreeNode} root
  3.  * @return {boolean}
  4.  */
  5. var isSymmetric = function(root) {
  6.   if (!root) return root
  7.   function isMirrorEqual(left, right) {
  8.     if (left === null && right === null) return true
  9.     if (left === null || right === null) return false
  10.     // 注意，这里比较的是 左节点的left和右节点的right， 左节点的right和右节点的left。 而不是同一个节点内的左右比较
  11.     return left.val === right.val && isMirrorEqual(left.left, right.right) && isMirrorEqual(left.right, right.left)
  12.   }
  13.   return isMirrorEqual(root.left, root.right)
  14. };

二叉树的最大深度

掌握遍历的套路

  • 只要遍历到这个节点既没有左子树，也没有右子树，说明就到底了，这时候如果之前记录了深度，就可以比较是否比之前记录的深度大，大就更新深度。
  • 依次类推，一直到最大深度。
    1. function maxDepth (root) {
    2.   if (!root) return root
    3. let ret = 1
    4. function compareDepth (root, depth) {
    5.   // 左右节点都没有，比较曾今的记录和传入的depth的较大者,不断更改外部变量ret，最后才能返回ret
    6.     if (!root.left && !root.right) ret = Math.max(ret, depth)
    7.   if (root.left) compareDepth(root.left, depth + 1)
    8.   if (root.right) compareDepth(root.right, depth + 1)
    9. }
    10. compareDepth(root, ret)
    11. // 被多次递归调用更新后, 返回的ret是最大的深度了
    12. return ret
    13. }
    精炼版
    1. function maxDepth (root) {
    2.   if (!root) return 0
    3. const left = root.left
    4. const right = root.right
    5. return Math.max(maxDepth(left), maxDepth(right)) + 1 // +1是因为每调用一次maxDepth，深度就会增加一层
    6. }

    将有序数组转化为高度平衡二叉搜索树

给一个整数数组nums，其中元素已经按升序排序，请将其转换为一颗高度平衡的二叉搜索数。

高度平衡的二叉搜索数是一颗满足 「每个节点的左右两个子树的高度差的绝对值不超过1」的二叉树

注意是，高度差不超过1
示例1：

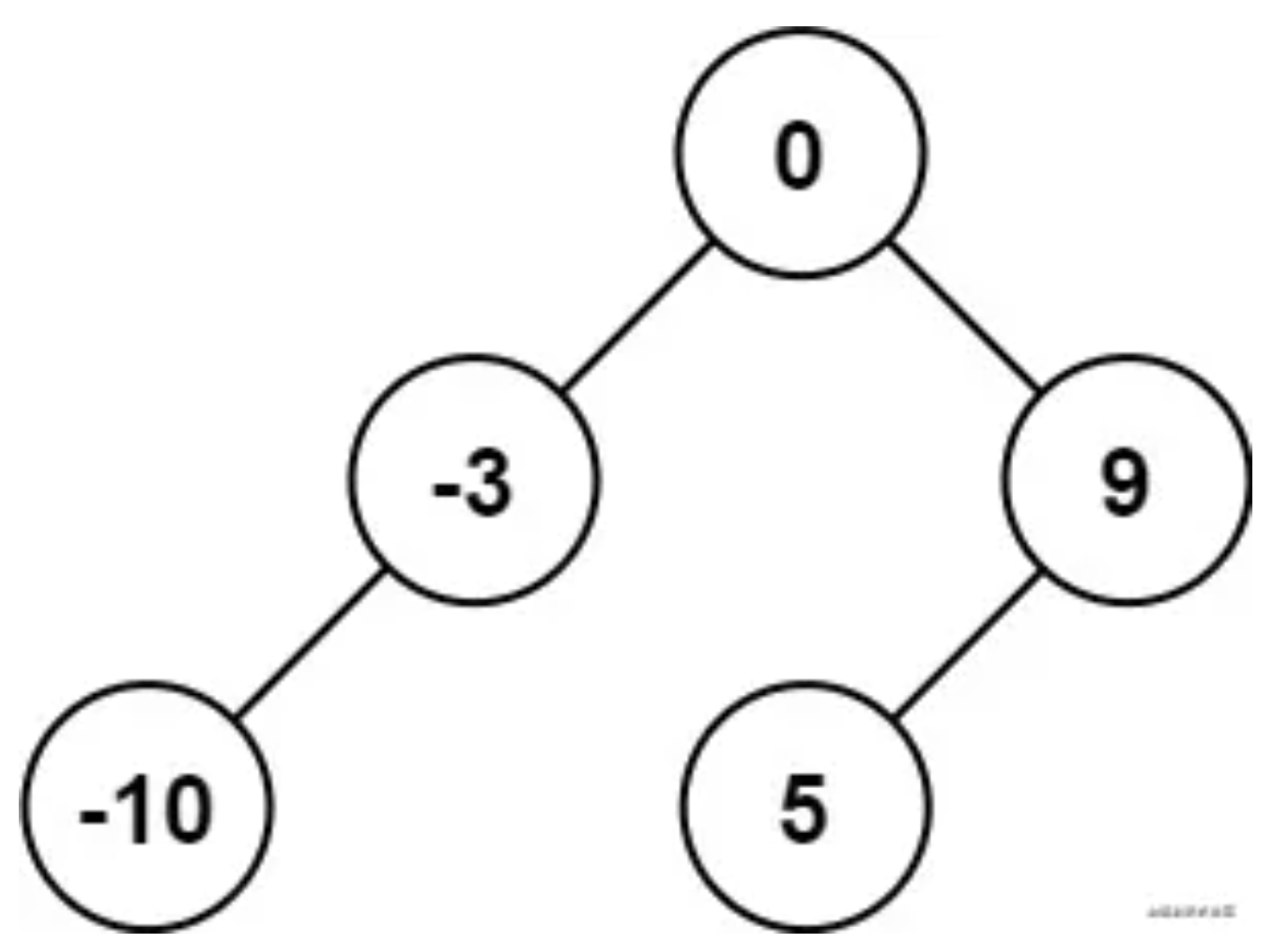
image.png
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案

示例2：
image.png
输入：nums = [1,3]
输出：[3,1]
解释：[1,3] 和 [3,1] 都是高度平衡二叉搜索树。

思路：

  • 构建一棵树包括： 构建root，构建root.left , root.right
  • 题目要求 ‘高度平衡’, 构建root的时候，选择数组的中间元素作为 root 节点值，即可保持平衡。
  • 递归函数可以传递数组，也可以传递指针，传递指针的时候l r 分别代表参与构建的二叉搜索树的数组的首尾索引
  1. // [-10,-3,0,5,9, 10, 13,15,17,18,20,33,34,45,66,77,88,99,100]
  2. // 我这种方法比较常规，每次对数组进行取出中间点，然后树的值为这个中间点的值。
  3. // 然后分割成两个数组再次进行上述操作
  4. function TreeNode (val) {
  5.     this.val = val
  6. }
  7. function createNode (arr) {
  8.   if (!arr.length || arr.length < 2) return arr[0] || null
  9.   const midIndex = Math.floor(arr.length / 2)
  10.     const mid = arr[midIndex]
  11.   const root = new TreeNode(mid)
  12.   root.left = createNode(arr.slice(0, midIndex))
  13.   root.right = createNode(arr.slice(midIndex + 1, arr.length))
  14.   return root
  15. }

最后可以得到
18
/ \
9 66
/ \ / \
0 15 34 99
/ \ / \ / \ / \
-3 5 13 17 33 45 88 100
/ / / /
-10 10 20 77

  1. // 另一种算法
  2. const sortedArrayToBST = function (nums) {
  3.     return toBST(nums, 0, nums.length - 1)
  4. }
  5. // l, r是传入的左右索引
  6. const toBST = function (nums, l, r) {
  7.     if (l > r) return null
  8.   // 移位操作，先转成二进制，然后整体向右移动一位。是取中间值的快捷操作
  9.   // js 二进制十进制互转 5.toString(2) <=> parseInt('0101', 2)
  10.   const mid = l + r >> 1
  11.   const root = new TreeNode(arr[mid])
  12.   root.left = toBST(nums, l, mid - 1) // 这里就不用改变数组，而是改变左右索引的位置
  13.   root.right = toBST(nums, mid + 1, r)
  14.   return root
  15. }

反转二叉树

翻转一棵二叉树。

示例：

输入：

  1.  4<br />   /   \<br />  2     7<br /> / \   / \<br />1   3 6   9

输出：
4
/ \
7 2
/ \ / \
9 6 3 1
备注:
这个问题是受到 Max Howell 的 原问题 启发的 ：

谷歌：我们90％的工程师使用您编写的软件(Homebrew)，但是您却无法在面试时在白板上写出翻转二叉树这道题，这太糟糕了。

结题思路：
二叉树肯定要从根节点开始对整棵树进行递归的遍历，解题中我们只需要关注一个节点的情况，然后对各个节点递归调用。
这个节点可能为null，可能其左右节点为null，分别处理。
最终仍要返回这个root，只不过是修改后的了。

  1. /**
  2.  * Definition for a binary tree node.
  3.  * function TreeNode(val) {
  4.  *     this.val = val;
  5.  *     this.left = this.right = null;
  6.  * }
  7.  */
  8. /**
  9.  * @param {TreeNode} root
  10.  * @return {TreeNode}
  11.  */
  12. var invertTree = function(root) {
  13.     if (!root || !root.val) return root
  14.     if (root.left || root.right) {
  15.         [root.left, root.right] = [root.right, root.left]
  16.         if (root.left) invertTree(root.left)
  17.         if (root.right) invertTree(root.right)
  18.     }
  19.     return root
  20. };

合并二叉树

给定两个二叉树，想象当你将它们中的一个覆盖到另一个上时，两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。
示例 1:
输入:
Tree 1 Tree 2
1 2
/ \ / \
3 2 1 3
/ \ \
5 4 7
输出:
合并后的树:
3
/ \
4 5
/ \ \
5 4 7
注意: 合并必须从两个树的根节点开始。

思路 两个值都为null，返回null 一个是null，则返回非null的值 两个都非null，值相加。其左右也相加

  1. // 深度优先
  2. /**
  3.  * Definition for a binary tree node.
  4.  * function TreeNode(val) {
  5.  *     this.val = val;
  6.  *     this.left = this.right = null;
  7.  * }
  8.  */
  9. /**
  10.  * @param {TreeNode} t1
  11.  * @param {TreeNode} t2
  12.  * @return {TreeNode}
  13.  */
  14. function mergeTrees (t1, t2) {
  15.   if (!t1 || !t2) return t1 || t2
  16.   t1.val += t2.val
  17.   t1.left = mergeTrees(t1.left, t2.left)
  18.   t2.right = mergeTrees(t2.right, t2.right)
  19.   return t1
  20. }
  1. // 广度优先
  2. // 把两个节点都放入队列，然后取出节点累加，然后再看它们的左右节点，如果存在，则继续放入队列中。
  3. function mergeTrees (t1, t2) {
  4.     if (!t1 || !t2) return t1 || t2
  5.   let queue = [ [t1, t2] ]
  6.   while(queue.length) {
  7.     const [ h1, h2 ] = queue.shift() // 每次取出一个来处理
  8.     const { left: l1, right: r1 } = h1
  9.     const { left: l2, right: r2 } = h2
  10.     h1.val += h2.val
  11.     if (l1 && l2) queue.push([l1, l2])
  12.     if (r1 && r2) queue.push([r1, r2])
  13.     if (!l1 && l2) h1.left = h2.left  // l1存在l2不存在的情况不用处理 
  14.     if(!r1 && r2) h1.right = h2.right
  15.   }
  16.   return t1 
  17. }

广度优先
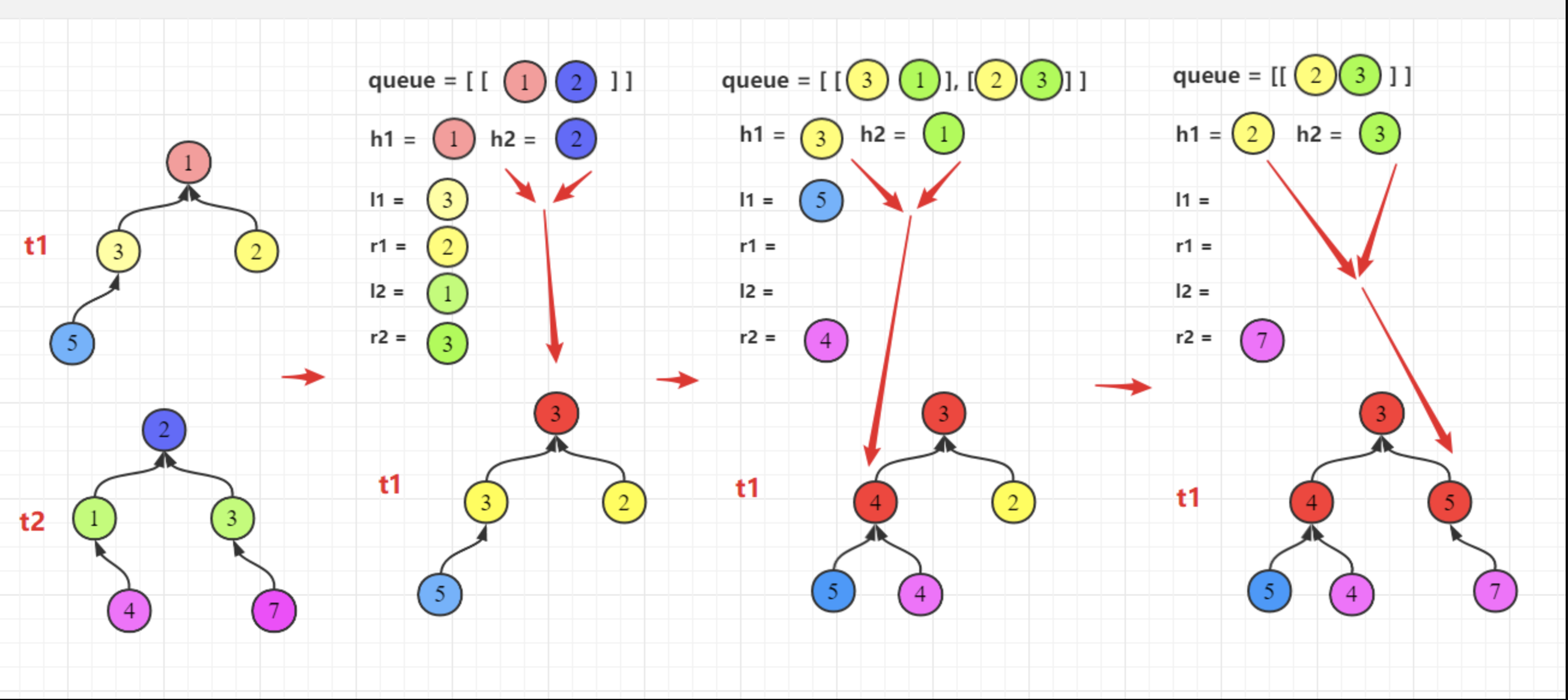
image.png

二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

  1. 3<br />   / \<br />  9  20<br />    /  \<br />   15   7<br />返回它的最大深度 3 。

原题链接

思路：仍然是递归的方式，
这个深度其实是从下而上计算的。从终止层的0开始，每层+1， 一直加到最顶端。

  1. /**
  2.  * Definition for a binary tree node.
  3.  * function TreeNode(val, left, right) {
  4.  *     this.val = (val===undefined ? 0 : val)
  5.  *     this.left = (left===undefined ? null : left)
  6.  *     this.right = (right===undefined ? null : right)
  7.  * }
  8.  */
  9. /**
  10.  * @param {TreeNode} root
  11.  * @return {number}
  12.  */
  13. var maxDepth = function(root) {
  14.     if (!root) return 0
  15.     const left = root.left
  16.     const right = root.right
  17.     return Math.max(maxDepth(left), maxDepth(right)) + 1
  18. };

BFS写法

  1. const maxDepth = (root) => {
  2.   if (root == null) return 0;
  3.   const queue = [root];
  4.   let depth = 1;
  5.   while (queue.length) {
  6.     // 当前层的节点个数
  7.     const levelSize = queue.length;          
  8.     // 逐个让当前层的节点出列
  9.     for (let i = 0; i < levelSize; i++) {    
  10.       // 当前出列的节点
  11.       const cur = queue.shift();            
  12.       // 左右子节点入列
  13.       if (cur.left) queue.push(cur.left);
  14.       if (cur.right) queue.push(cur.right); 
  15.     }
  16.     // 当前层所有节点已经出列，如果队列不为空，说明有下一层节点，depth+1
  17.     if (queue.length) depth++;
  18.   }
  19.   return depth;
  20. };
  22. 作者：xiao_ben_zhu
  23. 链接：https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/solution/liang-chong-jie-fa-di-gui-dfs-bfs-by-hyj8/