两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。
给出两个整数 x 和 y，计算它们之间的汉明距离。
注意：
0 ≤ x, y < 231.

输入: x = 1, y = 4 输出: 2

解释: 1 (0 0 0 1)

4 (0 1 0 0)

  1.    ↑   ↑

上面的箭头指出了对应二进制位不同的位置。

one-常规思路

思路：

  1. 将整数转换为二进制数
  2. 将二者位数补至一致
  3. 转化成数组，比较相同位置内容是否一致。
    1. // 首先：第一思路
    2. /**
    3. * @param {number} x
    4. * @param {number} y
    5. * @return {number}
    6. */
    7. // 转换成二进制
    8. function toBinary (value) {
    9.  return parseInt(value, 10).toString(2) // 转换成二进制
    10. }
    11. var hammingDistance = function(x, y) {
    12.  let binaryX = toBinary(x)
    13.  let binaryY = toBinary(y)
    14.  const distence = Math.abs(binaryX.length - binaryY.length)
    15.  const prefix =  Array(distence).fill('0').join('') // 位数需要位数补全的前缀
    16.  if (binaryX.length < binaryY.length) {
    17.      binaryX =  prefix + binaryX
    18.  } else {
    19.      binaryY =  prefix + binaryY
    20.  }
    21.  const arrX = binaryX.split('')
    22.  const arrY = binaryY.split('')
    23.  let diff = 0
    24.  for (let i = 0; i < arrX.length; i++) {
    25.      if (arrX[i] !== arrY[i]) {
    26.          diff += 1
    27.      }
    28.  }
    29.  return diff
    30. };

two-异或

  1. // 然后：想到异或 ^ 的功能，就是使数字的二进制位中同一位置相同是0， 不同是1, 将数字异或后转换成二进制,然后计算结果中1的个数即可
  2. /**
  3.  * @param {number} x
  4.  * @param {number} y
  5.  * @return {number}
  6.  */
  8. var hammingDistance = function(x, y) {
  9.     return (x ^ y).toString(2).split('').filter(e => e === '1').length
  10. }

three-移位

为了计算等于 1 的位数，可以将每个位移动到最左侧或最右侧，然后检查该位是否为 1。
更准确的说，应该进行逻辑移位，移入零替换丢弃的位。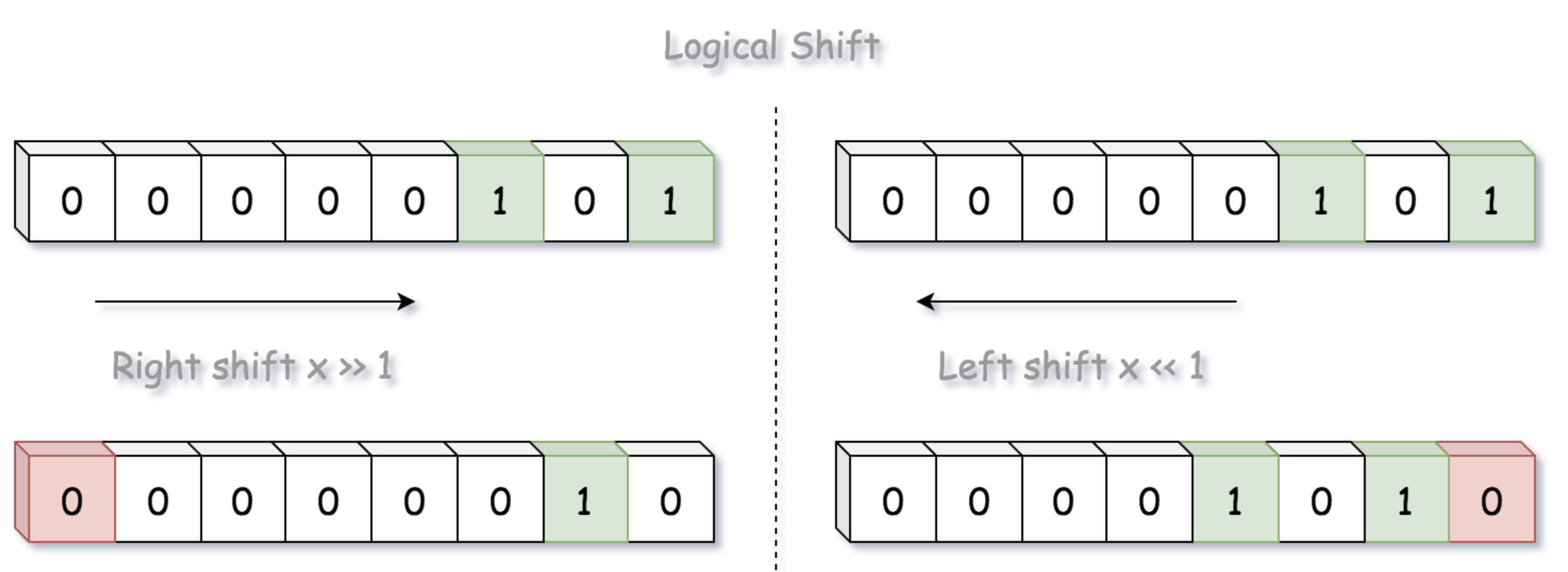
image.png
如果采用右移位，每个位置都会被移动到最右边。移位后检查最右位的位是否为 1 即可。检查最右位是否为 1，可以使用取模运算（i % 2）或者 AND 操作（i & 1），这两个操作都会屏蔽最右位以外的其他位。

  1. // 移位
  2. // 然后：想到异或 ^ 的功能，就是使数字的二进制位中同一位置相同是0， 不同是1, 然后统计异或后结果中的 1 的个数
  3. /**
  4.  * @param {number} x
  5.  * @param {number} y
  6.  * @return {number}
  7.  */
  9. var hammingDistance = function(x, y) {
  10.   let temp = x ^ y
  11.   let diff = 0
  12.     while(temp) {
  13.       if (temp & 1) {
  14.         diff += 1
  15.     }
  16.     temp = temp >> 1
  17.   }
  18.   return diff
  19. }

Four-布莱恩·克尼根位计数算法

上面的方法是逐位移动，然后比较边缘位置是否为1，有没有一种能更快找出等于1 的位数的办法

能否像人类直观的计数比特为1的位数，跳过两个1之间的0位。 例如10001000，如果能在遇到最后边的1后，直接跳过中间的0到达下一个1，那么效率则会高很多 这就是布莱恩.克尼根位计数算法的思想。该算法使用特定的比特位和算数运算移除等于1的最右比特位。

当我们在number 与 number - 1上做 AND 位运算时，原数字 number 的最右边等于1的比特会被移除

通过number = number & (number -1 ) 的操作，每次都改变了 number的值，在number = 0 之前，能执行几次，就说明，有几个比特位数为1， 大大减少了循环次数。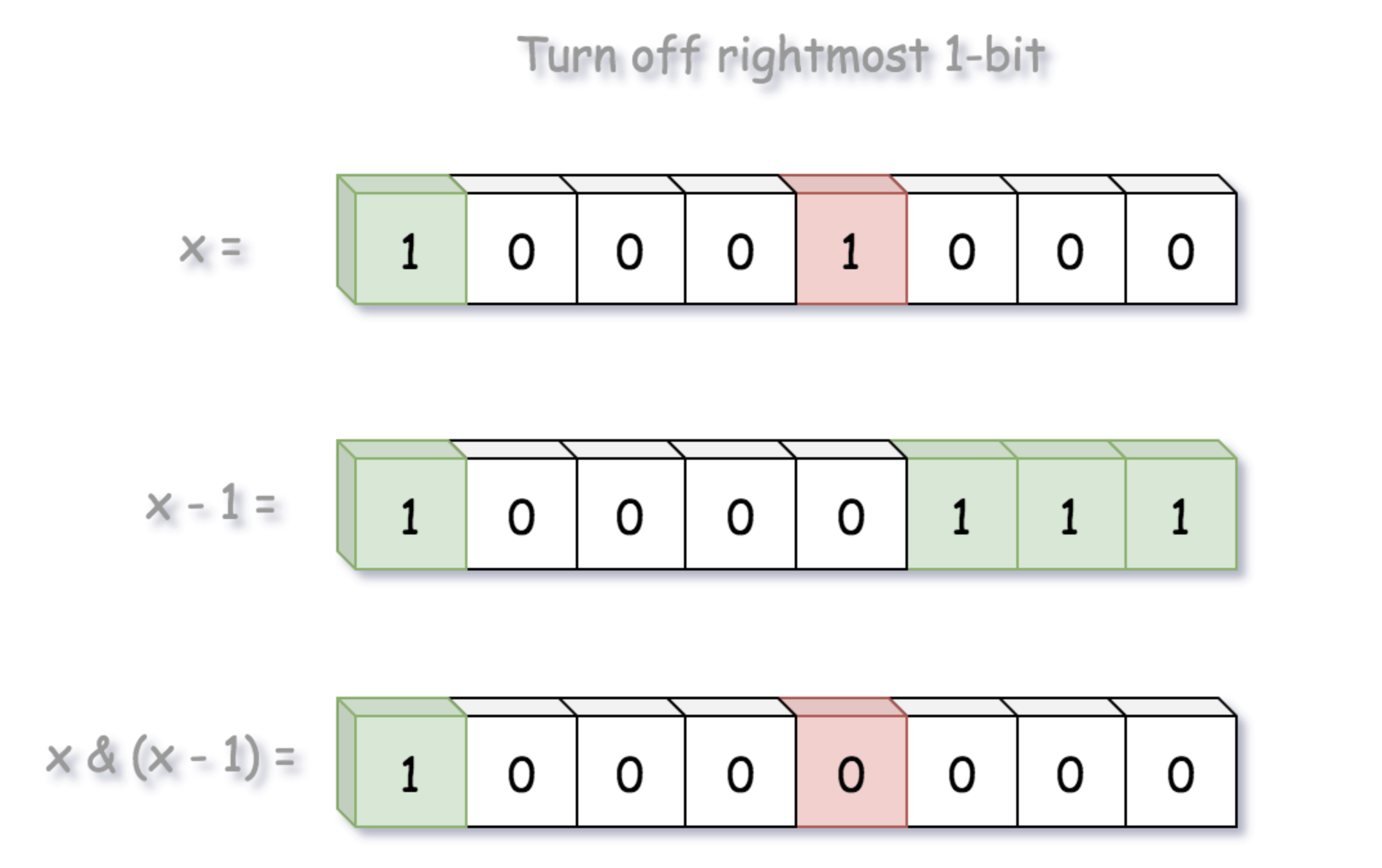
image.png

  1. // 布莱恩·克尼根位计数算法
  2. /**
  3.  * @param {number} x
  4.  * @param {number} y
  5.  * @return {number}
  6.  */
  8. var hammingDistance = function(x, y) {
  9.   let temp = x ^ y
  10.   let diff = 0
  11.     while(temp) {
  12.         diff += 1
  13.     temp = temp & (temp - 1)
  14.   }
  15.   return diff
  16. }