摘自： 链接

以下更多的是涉及数学问题，这些解法非常重要，因为在中级题里面会经常用到，比如我们马上讲到的加一这个题， 中级的两数相加都是一个模板。

加一

给定一个由 整数 组成的 非空 数组所表示的非负整数，在该数的基础上加一。
最高位数字存放在数组的首位， 数组中每个元素只存储单个数字。
你可以假设除了整数 0 之外，这个整数不会以零开头。

  1. 示例 1：
  2. 输入：digits = [1,2,3]
  3. 输出：[1,2,4]
  4. 解释：输入数组表示数字 123。
  6. 示例 2：
  7. 输入：digits = [4,3,2,1]
  8. 输出：[4,3,2,2]
  9. 解释：输入数组表示数字 4321。
  11. 示例 3：
  12. 输入：digits = [0]
  13. 输出：[1]
  1. // 转换成数字加1 然后再转成数组
  2. function addOne (arr) {
  3.     return String(Number(arr.join('')) + 1).split('').map(e => Number(e))
  4. }

虽然上述方法也能实现要求，但是这道题考察的两数相加的套路。

这个题有两个关键点：

  • 需要一个进位的变量carry来记录进位到底是几
  • 还需要一个每次迭代都重置和的变量sum来帮我们计算是否进位，以及进位后的数字

记住这个题，就是两数字相加的套路，这次是+1，下次就是两数相加的题

  1. function addOne (digits) {
  2.     let carry = 1 // 进位，由于是+1，那么这次初始进位直接是1。 如果是其他两数相加，这里carry应该是0，等待相同位的数相加后赋值
  3.   for(let i = digits.length - 1; i >= 0; i--) {
  4.       let sum = 0 // 每次循环都计算当前数和carry之和
  5.     sum = digits[i] + carry 
  6.     digits[i] = sum % 10 // 模运算取个位数
  7.     carry = (sum / 10) | 0 // 除以10然后 | 0 进行取整，赋给carry，这样每次循环carry就更新了。
  8.   }
  9.   if (digits[0] === 0) digits.unshift(carry) // 如果第一位是0，说明第一位进位了，需要加上进位
  10.   return digits
  11. }

tips: 按位或 |
2.1 | 0 或者 ~~2.1 都可以实现取整，但是都有限制。常见位运算，见本系列 JS常用位运算 it only works up to 2^31−1 which is around 2 billion (10^9). The max Number value is around 10^308

x的平方根

题目如下： 实现 int sqrt(int x) 函数。
计算并返回 x 的平方根，其中 x 是非负整数。
由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

  1. 输入: 4
  2. 输出: 2
  5. 输入: 8
  6. 输出: 2
  7. 说明: 8 的平方根是 2.82842..., 
  8.      由于返回类型是整数，小数部分将被舍去。

这道题是典型的 二分法 解题，所以我们需要熟悉二分法的通用模板，我们出一个题：
在 [1, 2, 3, 4, 5, 6] 中找到 4，若存在则返回下标，不存在返回-1

  1. // [1,2,3,4,5,6] 本题是已经排好序的，可能有些还要先排序
  2. function findIndex (arr, target) {
  3.     let [l, r] = [0, arr.length - 1] // 取出左右下标
  4.   while (l <= r) {
  5.     // 取中间值应放在while内，因为每次改变了l, r 后，都会重新二分划定区间。
  6.     // 而且如果mid不变化,l,r 也不会变化就不会退出循环了
  7.      const mid = l + r >> 1
  8.       if (arr[mid] === target) return mid
  9.     if (arr[mid] < target) {
  10.         l = mid + 1
  11.     } else {
  12.       r = mid - 1
  13.     }
  14.   }
  15.   return -1
  16. }

所以上面的平方根的问题其实是，找出一个数字，其平方最接近X，也可以运用 二分法 查找。
所以解题思路跟上面这个类似：

  1. // 找出X的平方根，返回整数，小数将被舍弃
  2. function getSqrt (x) {
  3.     let [l, r] = [0, x]
  4.   let temp = -1
  5.   while (l <= r) {
  6.       const mid = l + r >> 1
  7.     if (mid * mid === x) return mid
  8.     if (mid * mid < x) {
  9.       temp = mid // 因为是向下取整，最终mid*mid 肯定是小于x的,每次迭代时都记录下这个值，最后退出迭代的时候的那个值，就是目标值
  10.         l = mid + 1
  11.     } else {
  12.         r = mid - 1
  13.     }
  14.   }
  15.   return temp
  16. }

Excel表序列号

这题比较重要，也比较基础，简而言之就是进制转换，必须牢记

给你一个整数 columnNumber ，返回它在 Excel 表中相对应的列名称。

例如

  1. A -> 1
  2. B -> 2
  3. C -> 3
  4. ...
  5. Z -> 26
  6. AA -> 27
  7. AB -> 28 
  8. ...
  10. 示例 1：
  11. 输入：columnNumber = 1
  12. 输出："A"
  14. 示例 2：
  15. 输入：columnNumber = 28
  16. 输出："AB"
  18. 示例 3：
  19. 输入：columnNumber = 701
  20. 输出："ZY"
  22. 示例 4：
  23. 输入：columnNumber = 2147483647
  24. 输出："FXSHRXW"

这就是一道26进制的问题，我们10进制转26进制是不断的除以2，把余数加起来，26进制也是同样道理。

将26进制转化成10进制
思路： FXSHRXW -> ?

  • 首先要理解的是，从 F -> X -> S -> H -> R -> X -> W, 每前进一位，都代表着 前面的值*26+当前值 , 比如 F代表6，X代表24，S代表19, 那么 FX 就是 6 * 26 + 24 = 180。 FXS就是 180*26 + 19 = 4699。 这跟十进制的逻辑是一样的 十进制 321 也就是 (310 + 2)10 + 1 得到的。
  • 字母所代表的值如何获取？ 主要是和字母A做比较，用当前字母的 ASCII 码的位置和 A的做比较。注意要加1，因为A在26进制中代表1。
  1. // 注意，这里的title中的字母必须都是大写，要是小写字母或者大小写混用，那可就不是26进制了。
  2. function titleToNum (title) {
  3.     let num = 0
  4.   for (let i = 0; i < title.length; i++) {
  5.       num = num * 26 + (title[i].charCodeAt() - 'A'.charCodeAt() + 1)
  6.   }
  7.   return num
  8. }

10进制转换成26进制
思路：

  • 将数字不断除以26，然后每次除的余数，就是的26进制中的所代表的数字
  • 一直除到结果为0结束
  • 将余数变成26进制的字母，可以根据 'A'.charCodeAt() + 余数 - 1， 然后 String.fromCharCode(num)
    1.    |   2147483647
    2. 26 |__________________________________ 余数 23 W
    3.       26 | 82595524
    4.        |______________________________ 余数 24 X
    5.           26 | 3176750
    6.              |_________________________ 余数 18 R
    7.               26 | 122182
    8.                  |____________________ 余数 8  H
    9.                  26 | 4699
    10.                     |_______________ 余数 19 S
    11.                       26 | 180
    12.                            |__________ 余数 24 X
    13.                               26 |    6    
    14.                               |_____ 余数 6  F
    15.                                  0
    16. 结果即 FXSHRXW
    1. function numToTitle (num) {
    2. const AinAscii = 'A'.charCodeAt()
    3. let temp = num
    4. let str = ''
    5.   while (temp > 0) {
    6.     const remainder = temp % 26
    7.   str = `${String.fromCharCode(AinAscii - 1 + remainder)}${str}`
    8.   temp = (temp - remainder) / 26
    9. }
    10. return str
    11. }
    12. // numToTitle(2147483647)  "FXSHRXW"
    13. // numToTitle(1) "A"

    阶乘中的零

    给定一个整数 n，返回 n! 结果尾数中零的数量。

  1. 示例 1:
  2. 输入: 3
  3. 输出: 0
  4. 解释: 3! = 6, 尾数中没有零。
  6. 示例 2:
  7. 输入: 5
  8. 输出: 1
  9. 解释: 5! = 120, 尾数中有 1 个零.

这道题其实是数有多少个5， 有多少个 5 就有多少个 0。
比如说 5! = 5*4*3*2*1 = 120 , 其结果只有一个0，怎么产生的呢？ 因为25构造了一个0 。
能构成0的都必须要有5的参与，比如 25 45 65 等等
再看 10！= 10*9*8*7*6*5*4*3*2*1 = 3628800 , 其中 10 = 25 ，还有本身一个25， 两个5，结果里两个0。

我们再进一步，按照上面的说法，我们需要计算比如10的阶乘有多少个0，要把10的阶乘算出来，其实我们只需要算10有几个5就好了，为什么呢
因为我们发现只有5的倍数的阶乘，才会产生0，所以看阶乘数最多可以由多少个5组成就行了。
比如 阶乘数是 15， 那么就是3个5组成， 结果里有三个0。15！= 1307674368000
比如阶乘数是 12， 最多两个5组成，结果应该有2个0。 12！= 479001600

  1. function trailingZeroes (n) {
  2.     let num = 0
  3.   while (n > 1) {
  4.       n = (n / 5) >> 0
  5.     num += n
  6.   }
  7.   return num
  8. }

颠倒二进制位

颠倒给定的 32位无符号整数的二进制位

  1. 输入: 43261596
  2. 输出: 964176192
  3. 解释: 输入的二进制串 00000010100101000001111010011100 表示无符号整数 ，
  4.      因此返回 964176192，其二进制表示形式为 00111001011110000010100101000000。
  1. 输入：4294967293
  2. 输出：3221225471
  3. 解释：输入的二进制串 11111111111111111111111111111101 表示无符号整数 4294967293，
  4.      因此返回 3221225471 其二进制表示形式为 10111111111111111111111111111111 。

这类题就是反转字符串，可以把它转为字符串，再转成数组然后reverse一下。这里我们不使用字符串的方式，而是采用数学的方式来解答。
解答这道题需要一些前置知识：

与运算(按位与) &

&以特定的方式组合操作二进制数中对应的位，如果对应的位都为1，那么结果就是1， 如果任意一个位是0 则结果就是0

  1. 1 & 1 // 1的2进制最后一位是1，得到1
  2. 2 & 0 // 2的2进制最后一位是0，得到0
  3. 3 & 1 // 3的2进制最后一位是1，得到1
  4. 4 & 0 // 4的2进制最后一位是0，得到0

所以我们知道了10进制的最后一位的二进制是几。奇数是1，偶数是0。
JS使用32位按位运算数 （即我们的按位运算都会转成32位，你的十进制数字不能超过 232 大小，否则就有问题）

  • JS将数组存储为64位浮点数，但是所有的位运算都已32位二进制数执行。
  • 在执行位运算之前，JS将数组转换为32位有符号整数
  • 执行位运算操作后，结果转换回64位 JS 数。

移位运算 << 和 >>

<< 1 这个操作就是二进制整体向左移动移位，右侧补0 。右侧补0，其实在十进制上表现就是 这个十进制数乘以2
比如 2 << 1，2的二进制表示为 10 向左移1位，右侧补0 变成 二进制 100，即十进制4
4 << 1，4的二进制表示为 100, 向左移动1位，右侧补0， 为 1000, 即十进制8

同理， >> 1 就是二进制位整体向右移动1位，左侧补0， 在十进制表现上也就是除以2。 所以会有取平均值的操作 l + r >> 1

思路： 循环取最后一位拼接起来即可

  1. function reverseBits (n) {
  2.     let result = 0
  3.   for (let i = 0; i < 32; i++) {
  4.       result = (result << 1) + (n & 1)
  5.     console.table({ result, 'n&1': n & 1, n, 'n的二进制':Number(n).toString('2')})
  6.     n = n >> 1
  7.   }
  8.   // 为什么要 >>> 0 呢，一位javascript没有无符号整数，全是有符号的
  9.   // 不>>>0的话，得出来的值是负数，但是无符号整数是没有符号的
  10.   // javascript 有符号转化为无符号的方法就是>>>0
  11.   return result >>> 0
  12. }

整体思路是 不断取二进制的最后一位，然后放在前面。
难以理解的点在于，其中有个十进制与二进制之间转换的过程。第6行 n >> 1 向右移动1位，从二进制来说，是将暴露出一个新的末位。然后这个末位会和 1进行 按位与 &
& 1 的目的是让原来的二进制位保持原样。1&1 = 1， 0&1=0
前面已经说过，位运算是先转变成二进制，然后再转成js数字，那么我们在过程中，可以把他们n、result 这些都当做二进制来理解，虽然每一步的结果都被自动转成了js数。
所以 result 在向左移动，每次移动一位并在右边加上原来n的最右边一位。而n在向右移动，不断暴露出新的最右一位。当32次循环结束后，result里记录的就是原始n里二进制的倒序了。

整数反转

给你一个 32 位的有符号整数 x ，返回将 x 中的数字部分反转后的结果。
如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ，就返回 0。
假设环境不允许存储 64 位整数（有符号或无符号）

  1. 示例 1：
  2. 输入：x = 123 
  3. 输出：321
  5. 示例 2：
  6. 输入：x = -123
  7. 输出：-321
  9. 示例 3：
  10. 输入：x = 120
  11. 输出：21
  13. 示例 4：
  14. 输入：x = 0
  15. 输出：0

提示：

  • -231 <= x <= 231 - 1 ```javascript /**
    • 转字符串反转
    • @param {number} x
    • @return {number} */ var reverse = function(x) { const str = String(x) return Number(str.split(‘’).reverse().join(‘’)) };

/**

  • 末位弹出反转
  • @param {number} x
  • @return {number} / var reverse = function (x) { let n = 0 while (x !== 0) { // 每次弹出最后一位，存入新的一位 const digit = x % 10 x = (x / 10) >> 0 n = n 10 + digit // x是在安全数内的，这里要判断新的n是否也在安全数之内 // 注意这里的n 是在 2的正负31次方的区间内，而不是2的32次方 if (n > (Math.pow(2, 31) - 1 ) || n < Math.pow(-2, 31)) return 0 } return n } ```

    回文数

    给你一个整数 x ，如果 x 是一个回文整数，返回 true ；否则，返回 false 。 回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。例如，121 是回文，而 123 不是。

  1. 示例 1：
  2. 输入：x = 121
  3. 输出：true
  5. 示例 2：
  6. 输入：x = -121
  7. 输出：false
  8. 解释：从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。
  10. 示例 3：
  11. 输入：x = 10
  12. 输出：false
  13. 解释：从右向左读, 为 01 。因此它不是一个回文数。
  15. 示例 4：
  16. 输入：x = -101
  17. 输出：false

提示：

  • -231 <= x <= 231 - 1

首先最想想到的是转字符串，然后调转比较。
第二个想法是将数字本身反转，然后将反转后的数字与原始数字进行比较，如果它们是相同的，那么这个数字就是回文。
但是，如果反转后的数字大于 \text{int.MAX}int.MAX，我们将遇到整数溢出问题。
按照第二个想法，为了避免数字反转可能导致的溢出问题，为什么不考虑只反转 \text{int}int 数字的一半？毕竟，如果该数字是回文，其后半部分反转后应该与原始数字的前半部分相同。
例如，输入 1221，我们可以将数字 “1221” 的后半部分从 “21” 反转为 “12”，并将其与前半部分 “12” 进行比较，因为二者相同，我们得知数字 1221 是回文。
所有负数不可能是回文数。大于0的且各位是0的也不是回文数，首先排除。
然后如何得知已经反转到数字的一半了？
由于整个过程我们不断将原始数字除以 10，然后给反转后的数字乘上 10，所以，当原始数字小于或等于反转后的数字时，就意味着我们已经处理了一半位数的数字了。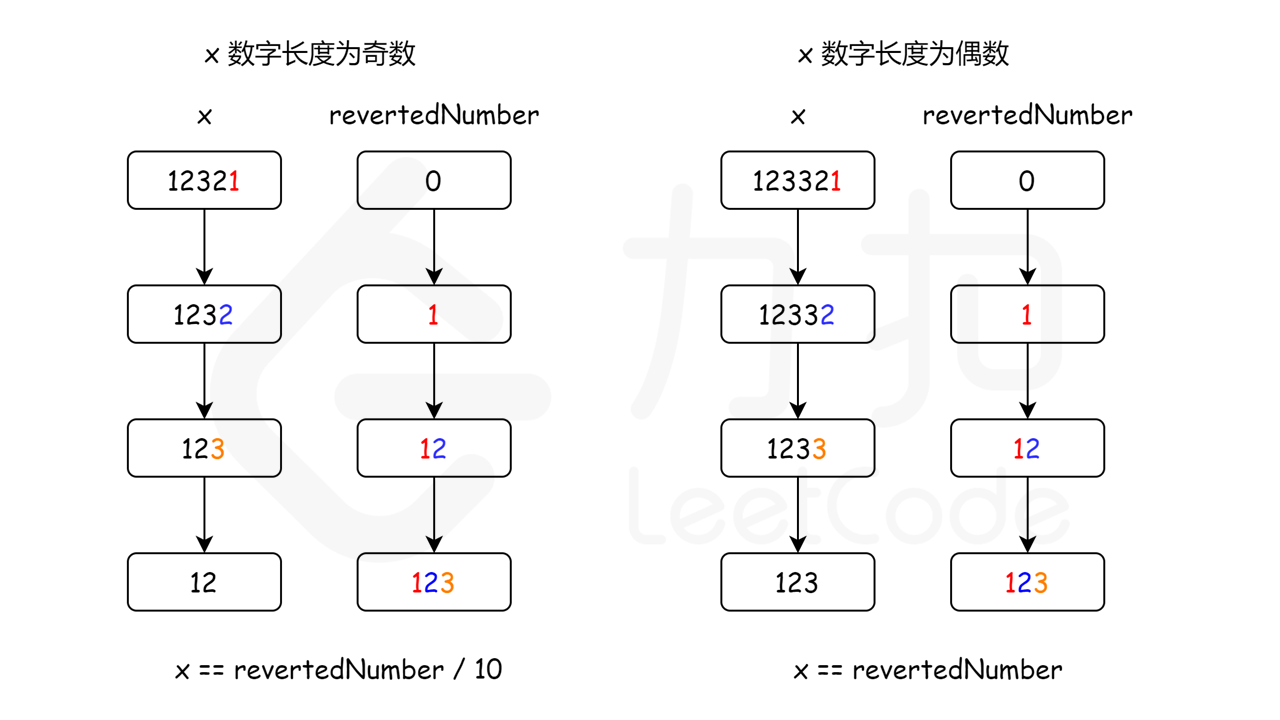
image.png

  1. /**
  2.  * @param {number} x
  3.  * @return {boolean}
  4.  */
  5. // 转字符串方式
  6. var isPalindrome = function (x) {
  7.   const str = x.split('').reverse().join('')
  8.   return str == x
  9. }
  12. // 颠倒位数判断相等
  13. // 不完善，可能在颠倒的过程中，超出了js安全数。就无法再继续判断了。
  14. var isPalindrome = function(num) {
  15.   let x = num
  16.   if (x < 0) return false
  17.   let temp = 0
  18.   while (x !== 0) {
  19.     const digit = x % 10
  20.     x = (x / 10) >> 0;
  21.     temp = temp * 10 + digit;
  22.     if (temp < Math.pow(-2, 31) || temp > (Math.pow(2, 31) - 1)) return false
  23.   }
  24.   return temp == num
  25. };
  28. // 进阶版，只颠倒数字后面一半即可判断
  29. var isPalindrome = function(x) {
  30.   if (x < 0 || ( x % 10 === 0 && x !== 0)) return false
  31.   let num = 0
  32.   while (x > num) {
  33.     const digit = x % 10
  34.     x = (x / 10) >> 0
  35.     num = num * 10 + digit
  36.   }
  37.   return x === num || x === (num / 10) >>> 0
  38. }

丢失的数字

给定一个包含 [0, n] 中 n 个数的数组 nums ，找出 [0, n] 这个范围内没有出现在数组中的那个数. 进阶： 你能否实现线性时间复杂度、仅使用额外常数空间的算法解决此问题?

这道题感觉题目不严谨

  1. 示例 1：
  3. 输入：nums = [3,0,1]
  4. 输出：2
  5. 解释：n = 3，因为有 3 个数字，所以所有的数字都在范围 [0,3] 内。2 是丢失的数字，因为它没有出现在 nums 中。
  7. 示例 2：
  9. 输入：nums = [0,1]
  10. 输出：2
  11. 解释：n = 2，因为有 2 个数字，所以所有的数字都在范围 [0,2] 内。2 是丢失的数字，因为它没有出现在 nums 中。

这题就是用0-n的总和减去数组总和

  • 0 - n 的总和用等差数列:（首数+尾数）* 项数 / 2 来求

    1. var missingNumber = function(nums) {
    2.   const len = nums.length
    4.  let sum = ((1 + len) * len) / 2
    6.  for (let i = 0; i < len; i++) {
    7.    sum -= nums[i]
    8.  }
    10.  return sum
    11. }

3的幂

给定一个整数，写一个函数来判断它是否是 3 的幂次方。如果是，返回 true ；否则，返回 false 。 整数 n 是 3 的幂次方需满足：存在整数 x 使得 n == 3的x次方 

  1. 示例 1：
  2. 输入：n = 27
  3. 输出：true
  5. 示例 2：
  6. 输入：n = 0
  7. 输出：false
  9. 示例 3：
  10. 输入：n = 9
  11. 输出：true

Fizz Buzz

写一个程序，输出从1到n数字的字符串表示，

  1. 如果n是3的倍数，输出 ‘Fizz’
  2. 如果n是5的倍数，输出’Buzz’
  3. 如果n同时是3和5的倍数，输出’FizzBuzz’
  1. // 实例 1
  2. 输入：n = 15
  3. 返回： [ "1","2","Fizz","4","Buzz","Fizz","7","8","Fizz","Buzz","11","Fizz","13","14","FizzBuzz"]
  1. function fizzBuzz (n) {
  2.     const list = [];
  3.     for (let i = 1; i <= n; i++) {
  4.       const is3Times = i % 3 === 0; // 是否是3的倍数
  5.       const is5Times = i % 5 === 0; // 是否是5的倍数
  6.       const is15Times = is3Times && is5Times; // 是否是15的倍数
  7.       if (is15Times) {
  8.         list.push('FizzBuzz');
  9.         continue;
  10.       }
  11.       if (is3Times) {
  12.         list.push('Fizz');
  13.         continue;
  14.       }
  15.       if (is5Times) {
  16.         list.push('Buzz');
  17.         continue;
  18.       }
  19.       list.push(`${i}`);
  20.     }
  21.     return list;
  22.   };

整数反转

给你一个32位无符号整数X，返回将x中的数字部分反转后的结果。 如果反转后整数超过32位的有符号整数的范围 [-232 , 232- 1 ], 就返回0 。 假设环境不允许存储64位整数 （有符号或无符号）

  1. 输入： x = 123
  2. 输出： 321
  4. 输入： x = -123
  5. 输出： -321
  7. 输入： x = 120
  8. 输出：21
  1. // 前面我们有过这种接法。这种是将n转换成二进制，然后二进制的位前后颠倒，再转成十进制的结果。本质是二进制位颠倒。跟本题有一些区别。
  2. function reverse (n) {
  3.     let temp = 0
  4.   for (let i = 0; i < 32; i++) {
  5.         temp = (temp << 1) + (n & 1)
  6.     n = n >> 1
  7.   }
  8.     return temp >>> 0
  9. }

本题可以从这种思路解析：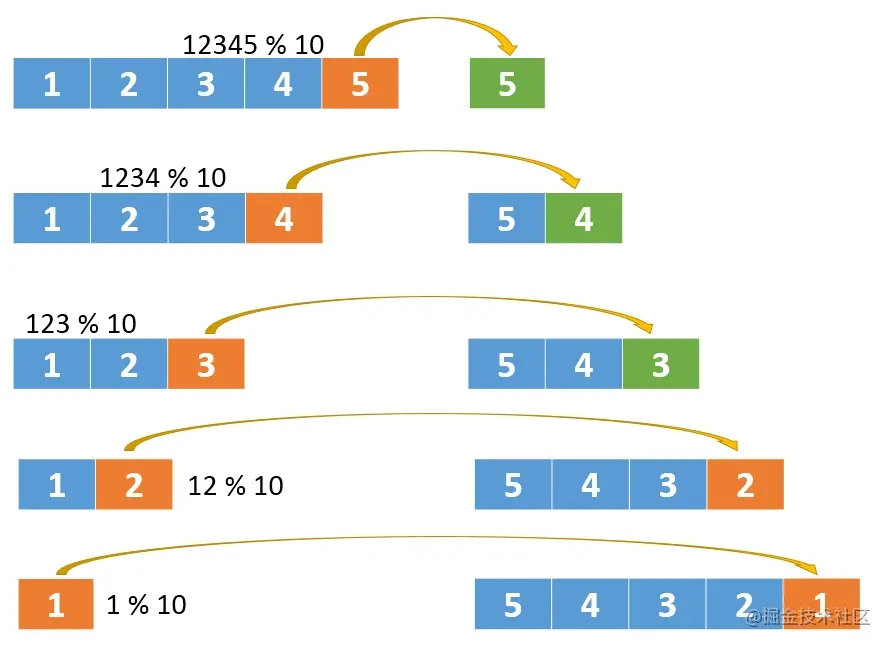
image.png

  1. function reverse (n) {
  2.   let temp = 0
  3.   while (n) {
  4.     temp = temp * 10 + n % 10
  5.       if (temp > Math.pow(2, 31) - 1 || temp < Math.pow(-2, 31)) return 0
  6.     n = (n / 10) | 0
  7.   }
  8.   return temp
  9. }