Hard
    mark: https://mp.weixin.qq.com/s/OE4lHO8-jOIxIfWO_1oNpQ

    给定两个升序数组， 如何找到两个数组归并之后的中位数 ?

    中位数，就是在数组中间位置的数。 如果数组长度为奇数，则中位数为中间的数。如果数组长度为偶数，则中位数为中间两数的平均值。

    把两个数字结合起来并排序，然后取中间位置的数/平均数。

    1. function getMid (arr1, arr2) {
    2.   const arr = [...arr1, ...arr2].sort((a, b) => a - b)
    3.   console.log(arr)
    4.   const mid = (0 + arr.length) / 2
    5.   // 偶数. 二者平均
    6.   if (!(mid % 1)) return (arr[mid] + arr[mid - 1]) /2
    7.   // 奇数。取整后取中间数字
    8.   return arr[mid >> 0]       
    9. }

    如果数组长度分别为m, n，则这样的时间复杂度和空间复杂度都是O(m+n)。 不够高效

    这题的思路是，既然最终是获取合并后数组的中位数，还不允许进行数组合并，那么就要在各自的数组中进行操作。
    每个数组都分成左右两部分，左边部分（较小），右边部分（较大）。

    理想情况是 两个数组的左部分结合起来正好是 归并数组中位数的左边。 右边部分结合起来是 归并数组中位数的右边。 （左右部分可能包括中位数）

    那么每个数组该如何确定左右部分的划分位置呢？ 是否有规律可循?

    其实可以注意到： 偶数情况下，两个数组的左边部分的元素个数之和， 应该是等于 右边元素个数之和的。
    假设俩数组分界点分别在i, j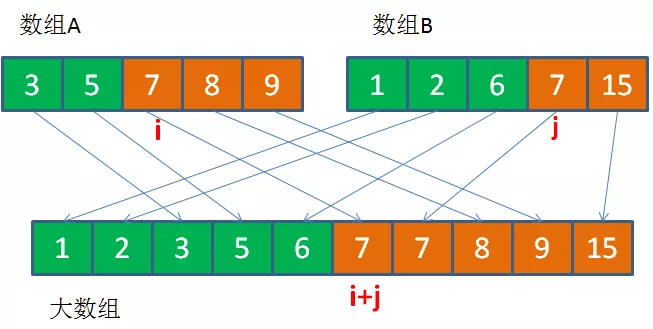
    image.png

    假设数组A的长度是m，绿色和橙色元素的分界点是i，数组B的长度是n，绿色和橙色元素的分界点是j，那么为了让大数组的左右两部分长度相等，则i和j需要符合如下两个条件：

    i + j = （m+n+1）/2（之所以m+n后面要再加1，是为了应对大数组长度为奇数的情况）

    Max(A[i-1],B[j-1]) < Min(A[i], B[j])
    (直白的说，就是最大的绿色元素小于最小的橙色元素)

    由于m+n的值是恒定的，所以我们只要确定一个合适的i，就可以确定j，从而找到大数组左半部分和右半部分的分界，也就找到了归并之后大数组的中位数。

    然后使用二分法对两个数组分别寻找i和j
    i和j满足约束条件 i + j = （m+n+1）/ 2
    然后
    验证i和j，分为下面三种情况：

    • B[j−1]≤A[i] && A[i−1]≤B[j] 说明i和j左侧的元素都小于右侧，这一组i和j是我们想要的。
    • A[i]<B[j−1] 说明i对应的元素偏小了，i应该向右侧移动。
    • A[i−1]>B[j] 说明i-1对应的元素偏大了，i应该向左侧移动。
    1. function findMedianSortedArrays (arr1, arr2) {
    2.     let l1 = arr1.length
    3.   let l2 = arr2.length
    4.   // 如果第一个数组比第二个长，则交换位置
    5.   if (l1 > l2) {
    6.       [arr1, arr2] = [arr2, arr1]
    7.     [l1, l2] = [l2, l1]
    8.   }
    9.   let start = 0
    10.   let end = l1
    11.   let mid = ((l1 + l2 + 1) >> 1) >> 0  // 合并后大数组的中位数的位置. 位运算先除2再取整
    12.   while (start <= end) {
    13.       let i = (start + end) >> 1 // arr1中间位置i
    14.     let j = mid - i // 则对应j的位置可以计算出来
    15.     // 如果arr1[i-1] < arr2[j] 并且 arr2[j-1] < arr1[i]，这是完美情况，两数组左侧都小于对方的标记位置的数。则中位数为 (arr1[i] + arr2[j]) /2
    16.     // 如果 arr1[i-1] > arr2[j], 说明i取大了，i往左移，在i+j和一定的情况下，j势必往右移
    17.     // 如果 arr2[j-1] > arr1[i], 说明取小了，i往右移动，同时j往左移动
    18.     if (i < end && (arr1[i] < arr2[j-1])) { // 因为向右移动，不能超出右边界
    19.         start = i + 1 // i 右移
    20.     } else if (i > start && arr1[i-1] > arr2[j]) { // 因为是向左移动，不能超出左边界
    21.         end = i - 1 // i 左移
    22.     } else {
    23.       // 双方的左部分都比对方的标记点小，那么这时候，将arr1, arr2左侧右侧分别合并，组成的大数组的中间值（一个或两个），就是中位数了。因为数组是升序排列的，所以还需要在各自的左侧中寻找到真正靠近中间位置的点,也就是arr1, arr2左部分中的最大的那个值， maxLeft.
    24.       // 同理，也需要找出两个右部分中真正靠近中间位置的数，也就是arr1, arr2的右部分里的最小的值， minRight。
    25.              let maxLeft, minRight
    26.         // 当arr1 所有元素都比 arr2 大，这时候i会一直移动到0位置
    27.       if (i === 0) {
    28.         maxLeft = arr2[j - 1] // 因为位置点元素arr2[j]被划分到了右部分，所以maxLeft就是j-1位置元素
    29.       }
    30.       // i移动到了最右端，说明arr1中所有元素都比arr2中小. 虽然移动到了最右侧，此时的maxLeft却不是一定是arr1[i - 1], 也可能是arr2[j - 1]. 
    31.       // i === arr1.length 和 j === 0 是两种情况.
    32.       // else if (i === arr1.length) {
    33.          //   maxLeft = arr1[i - 1]
    34.       // }
    35.       else if (j === 0) { // j能走到0，说明这种情况下，arr1元素都比arr2小，且最大的左侧元素就在arr1[i - 1]
    36.           maxLeft = arr1[i - 1]
    37.       } else {
    38.           maxLeft = Math.max(arr1[i - 1], arr2[j - 1])
    39.       }
    40.       // 如果合并后数组总长度为奇数，则此时的maxLeft就是中位数
    41.       if ((l1+l2) % 2 === 1 ) return maxLeft
    42.       // 同理计算minRight
    43.       if (i === l1) { // i右移到最右侧. 说明arr1所有元素都比arr2小，
    44.           minRight = arr2[j]
    45.       } else if (j === l2) { // j右移到了最右侧，说明arr1所有元素都比arr2大
    46.         minRight = arr1[i]
    47.       } else {
    48.         minRight = Math.min(arr1[i], arr2[j])
    49.     }
    50.       return (maxLeft + minRight) / 2
    51.   }
    52.     return 0
    53. }
    54. }