栈是限定仅在表尾进行插入和删除操作的**线性表**。
队列是只允许在一端进行插入操作、而在另一端进行删除操作的线性表。**
概念
栈(Stack),有些地方称为堆栈,是一种容器,可存入数据元素、访问元素、删除元素,它的特点在于只能允许在容器的一段(称为栈顶端指标,Top)进行加入数据(Push)和输出数据(Pop)的运算。没有了位置概念,保证任何时候可以访问、删除的元素都是此前最后存入的那个元素,确定了一种默认的访问顺序。
由于栈数据结构只允许在一端进行操作,因而按照后进先出(LIFO,Last In First Out)的原理运作。
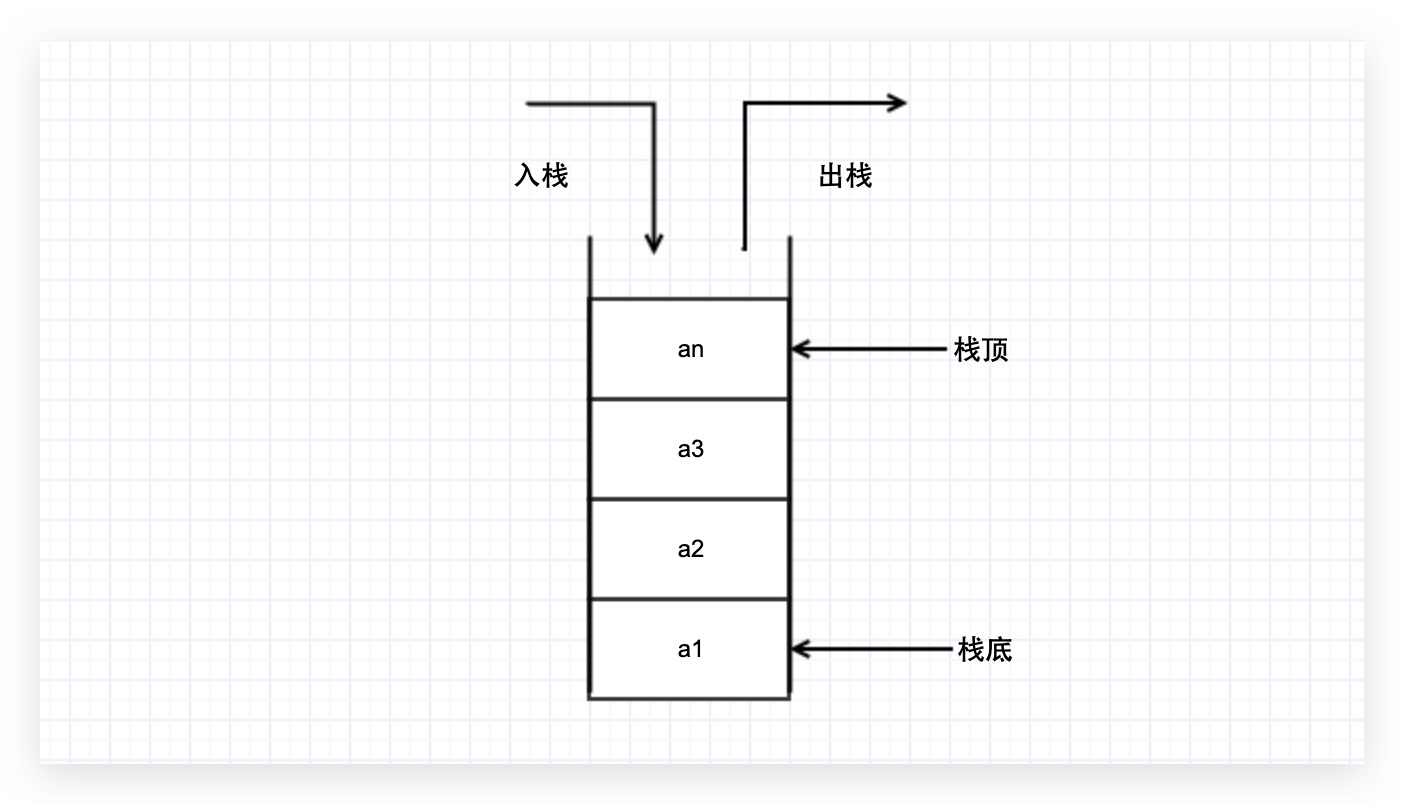
从栈的操作特性上来看,栈是一种“操作受限”的线性表,只允许在一端插入和删除数据。
栈既可以用数组来实现,也可以用链表来实现。
- 用数组实现的栈,我们叫作顺序栈
- 用链表实现的栈,我们叫作链式栈
时间复杂度
void push(e):O(1)均摊- 栈内存足够:O(1)
- 栈内存不够:需要重新申请内存,搬移数据,时间复杂度就是 O(n)
E pop():O(1) 均摊E peek():O(1)int getSize():O(1)boolean isEmpty():O(1)
也就是说,对于入栈操作来说,最好情况时间复杂度是 O(1),最坏情况时间复杂度是 O(n),那么均摊时间复杂度是多少呢?答案是O(1)。
均摊时间复杂度一般都等于最好情况时间复杂度。因为在大部分情况下,入栈操作的时间复杂度 O 都是 O(1),只有在个别时刻才会退化为 O(n),所以把耗时多的入栈操作的时间均摊到其他入栈操作上,平均情况下的耗时就接近 O(1)。
实现方式
- push 添加一个新的元素 item 到栈顶
- pop 弹出栈顶元素
- peek 返回栈顶元素
- isEmpty 判断栈是否为空
- size 返回栈的元素个数
栈的实际应用
函数调用栈
我们知道,操作系统给每个线程分配了一块独立的内存空间,这块内存被组织成“栈”这种结构, 用来存储函数调用时的临时变量。每进入一个函数,就会将临时变量作为一个栈帧入栈,当被调 用函数执行完成,返回之后,将这个函数对应的栈帧出栈。
在表达式求值中的应用
你知道编译器如何利用栈来实现表达式求值的吗?
为了方便解释,我将算术表达式简化为只包含加减乘除四则运算,比如:34+13*9+44-12/3。 对于这个四则运算,我们人脑可以很快求解出答案,但是对于计算机来说,理解这个表达式本身 就是个挺难的事儿。如果换作你,让你来实现这样一个表达式求值的功能,你会怎么做呢?
实际上,编译器就是通过两个栈来实现的。其中一个保存操作数的栈,另一个是保存运算符的 栈。我们从左向右遍历表达式,当遇到数字,我们就直接压入操作数栈;当遇到运算符,就与运 算符栈的栈顶元素进行比较。
如果当前运算符比运算符栈顶元素的优先级高,就将当前运算符压入栈;如果比运算符栈顶元素的优先级低 或者相同,从运算符栈中取栈顶运算符,从操作数栈的栈顶取 2 个操作数,然后进行计算,再 把计算完的结果压入操作数栈,继续比较。

