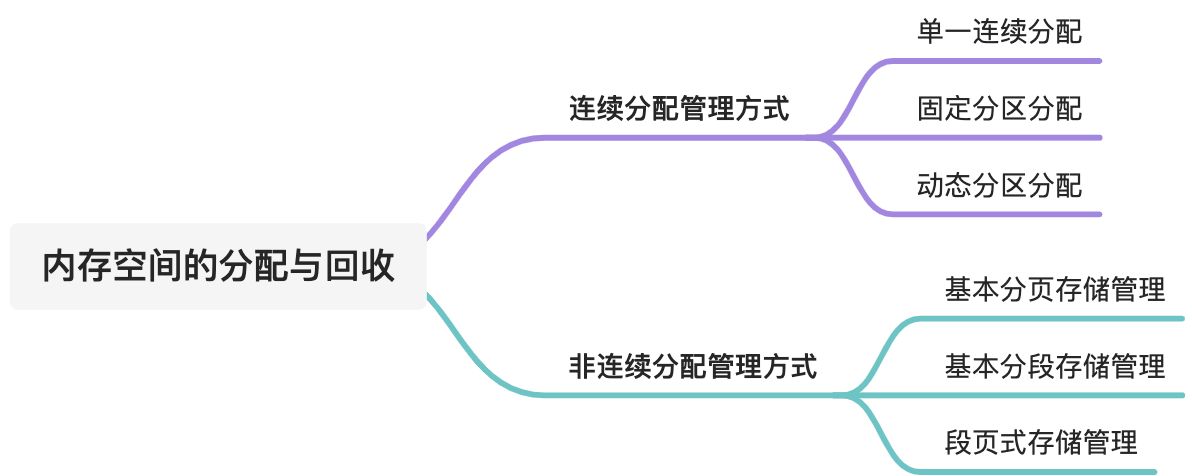
连续分配管理方式
连续分配:指为用户进程分配的必须是一个 连续的内存空间。
单一连续分配
在单一连续分配方式中,内存被分为 系统区 和 用户区。
- 系统区 常常位于内存的低地址部分,用于存放操作系统相关数据;
- 用户区 用于存放用户进程相关数据。
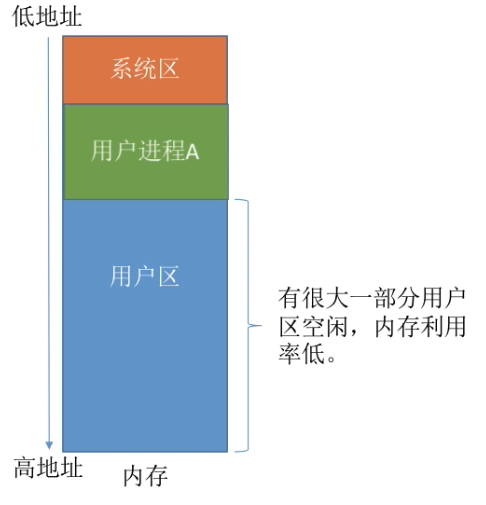
内存中 只能有一道用户程序,用户程序独占整个用户区空间。
- 优点:
- 实现简单;
- 无外部碎片;
- 可以采用覆盖技能扩充内存;
- 不一定需要采取内存保护(因为只有一道用户程序)
- 缺点:
- 只能用于单用户、单任务的操作系统中;
- 有内部碎片(没有用到的用户区);
- 存储器利用率极低
固定分区分配
为了可以装入多道程序,且这些程序之间又不会互相干扰,于是将整个 用户空间 划分为 若干个固定大小的分区,在 每个分区中只装入一道作业,这样就形成了最早的、最简单的一种可运行多道程序的内存管理方式。
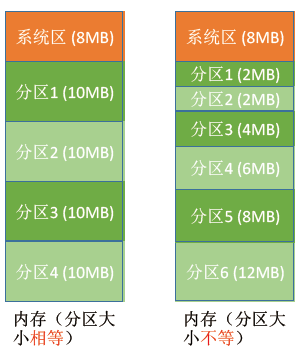
- 分区大小相等:缺乏灵活性,但是很 适合用于用一台计算机控制多个相同对象的场合
- 分区大小不等:增加了灵活性,可以满足大小不同的进程需求,根据常在系统中运行的作业情况进行划分(划分多个小分区、适量中等分区、少量大分区)
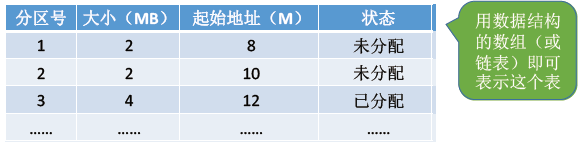
操作系统需要建立一个数据结构 —— 分区说明表,来实现各个分区的分配与回收。每个表项对应一个分区,通常按分区的大小排列。每个表项包括:分区的大小、起始状态、状态(是否分配)。
- 优点:
- 实现简单、无外部碎片
- 缺点:
- 当用户程序太大,可能没有一个分区满足要求,不得不采用覆盖技术,会降低性能
- 会产生内部碎片,内存利用率低
动态分区分配
动态分区分配(可变分区分配):不会预先分配分区,而是进程装入内存时,根据进程的大小动态地建立分区。
- 系统要用什么样的数据结构记录内存的使用情况?
- 当很多个空闲分区都能满足需求时,应该选择哪个分区进行分配?
- 如何进行分区的分配与回收操作?
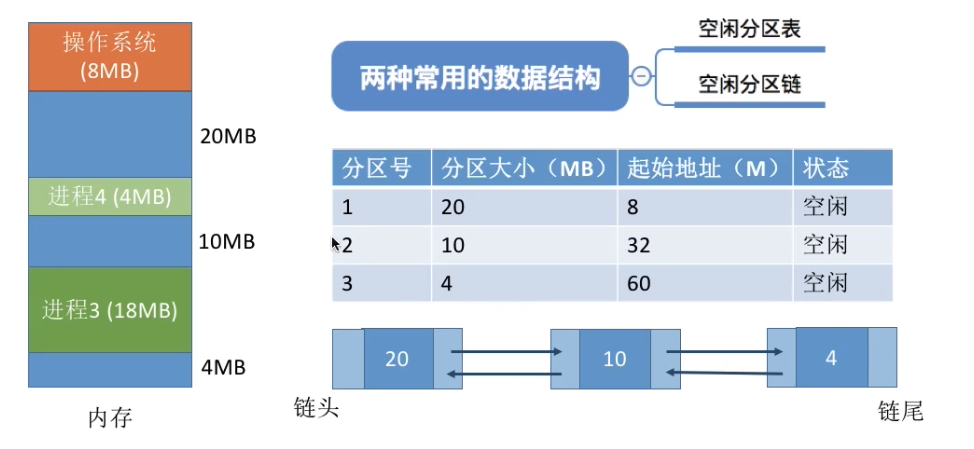
记录内存的数据结构
- 空闲分区表
- 空闲分区链
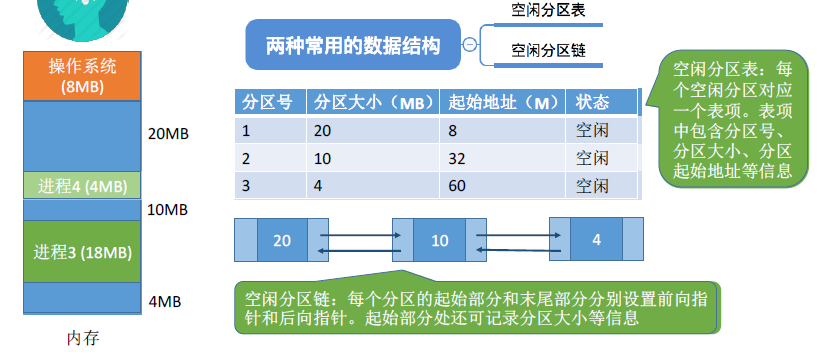
空闲分区的选择
把一个新作业装入内存时,须按照一定的动态分区分配算法,从空闲分区中选择一个分区分配给该作业。
可参考后面介绍的 四种算法。
分区的分配和回收
分配
- 情况一:当从空闲分区表中选择一个分区分配后,内存还有剩余,则修改表项
- 情况二:当从空闲分区表中选择一个分区分配后,刚刚好分配完,则删除该表项
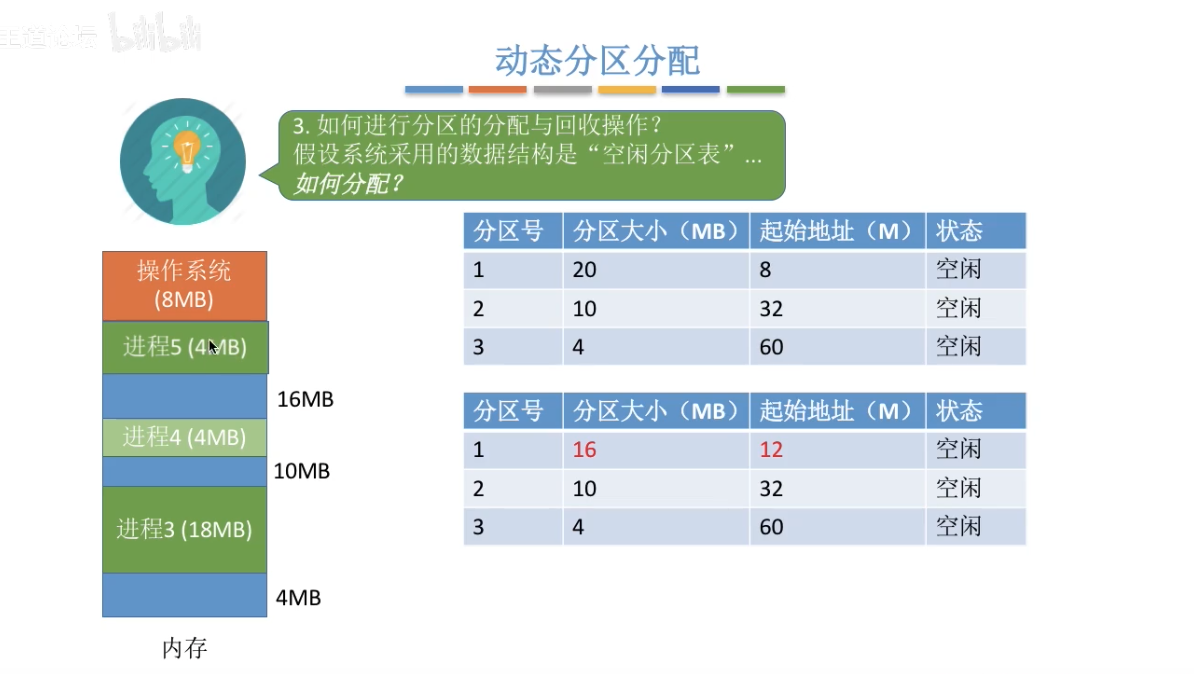
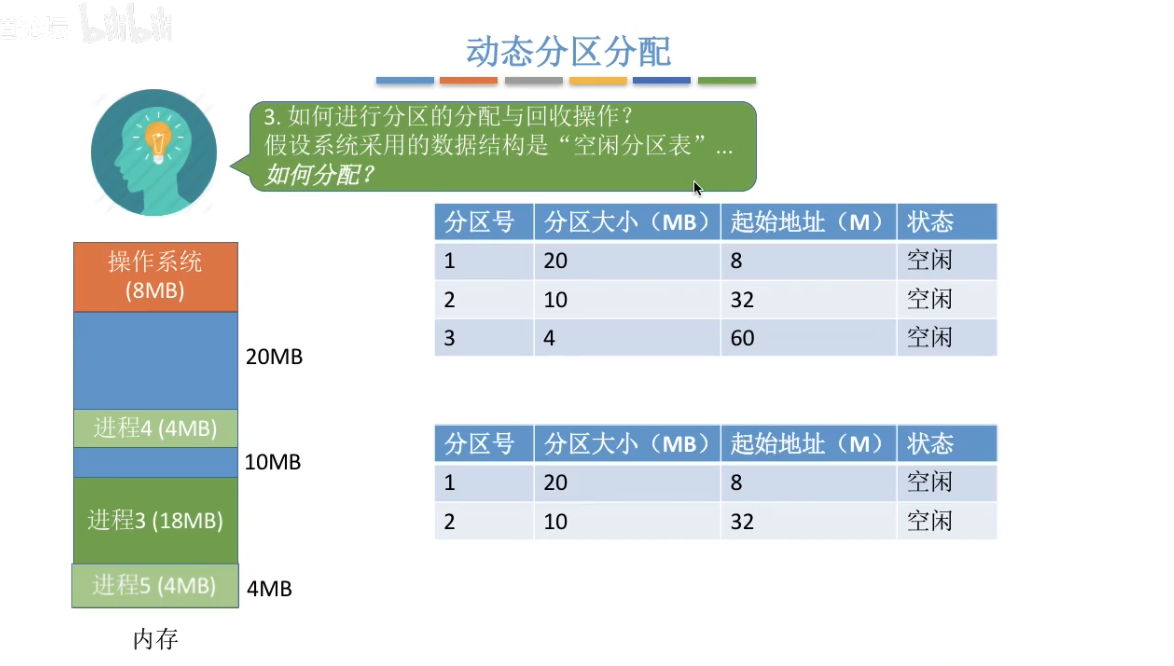
回收
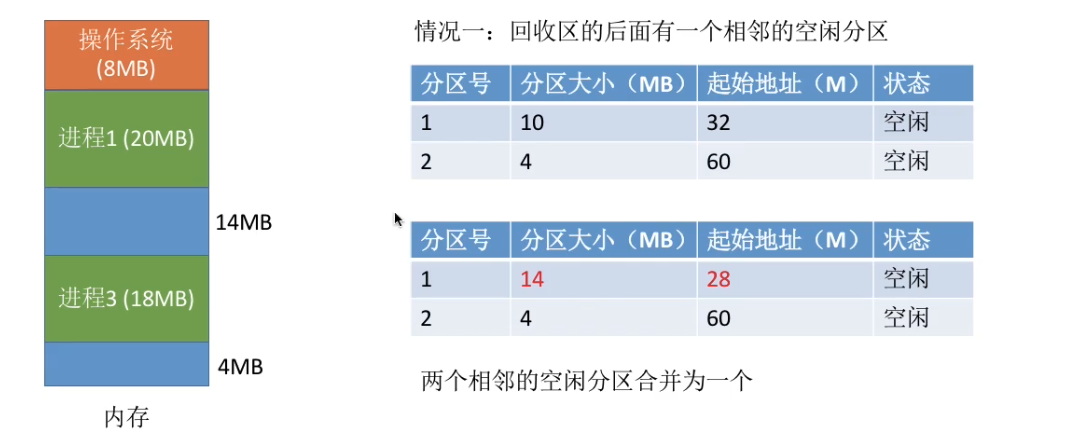
- 情况一:回收区后面有一个相邻的空闲分区,则合并
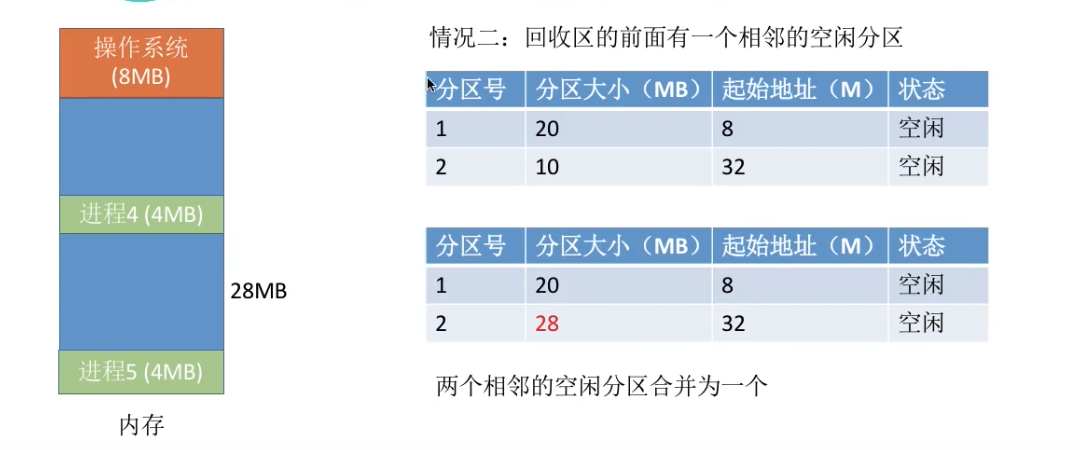
- 情况二:回收区前面有一个相邻的空闲分区,则合并
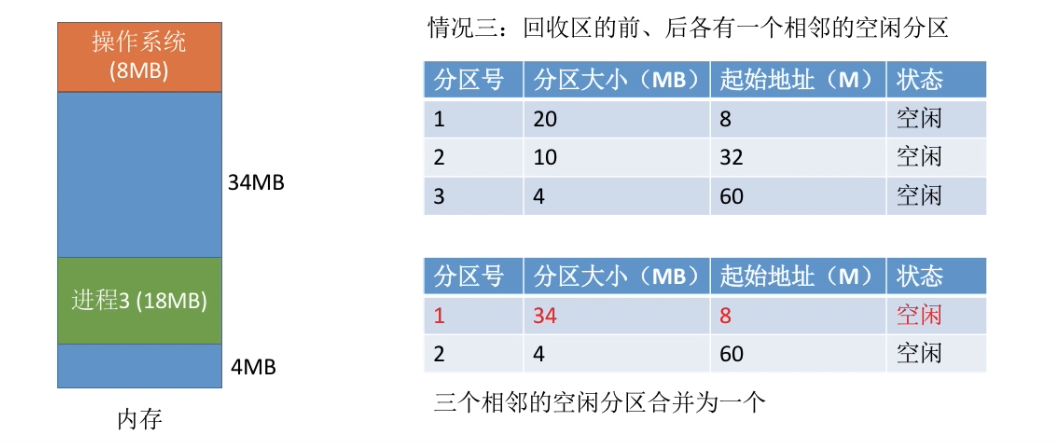
- 情况三:回收区前后各有一个相邻的空闲分区,则三个合并为一个
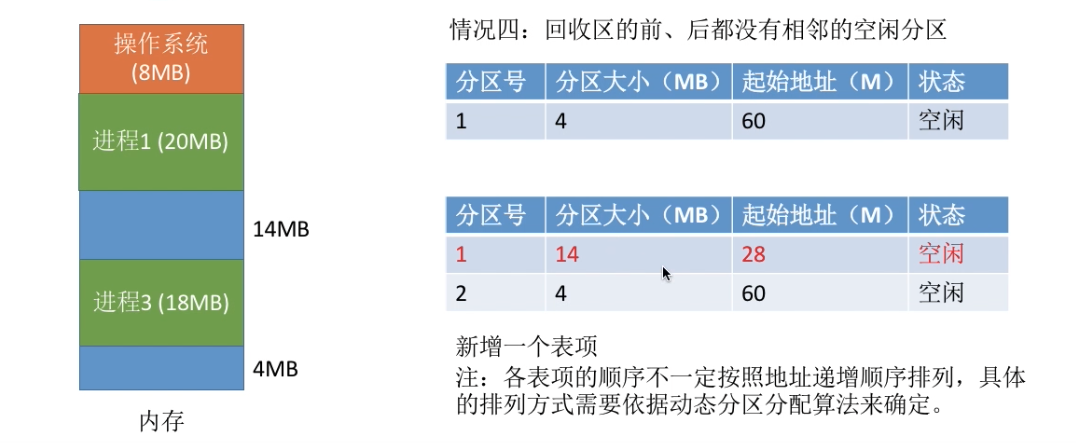
- 情况四:回收区前后无相邻的空闲分区,则新增一个表项
内部碎片:分配给某些进程的内存区域中,有些部分没有用上
外部碎片:内存中某些空闲的分区由于太小而难以利用
如果内存中零碎的空间太多,导致无法满足内存较大的进程,可采用 拼凑技术 来解决外部碎片
思考:动态分区分配应该使用动态重定位装入(绝对装入地址改变,需要重新编译;静态装入,不支持移动)
首次适应算法(First Fit)
算法思想:每次都从低地址开始查找,找到第一个能满足大小的空闲分区。
实现方法:空闲分区以地址递增的次序开始排序。每次分配内存时顺序查找 空闲分区链(或空闲分区表),找到第一个满足大小的空闲分区。
最佳适应算法(Best Fit)
算法思想:考虑大内存的进程有地可留,优先使用更小内存的空闲区
实现方法:空闲分区 按容量 递增次序链接。每次分配内存时顺序查找空闲分区链(或空闲分区表),找到第一个满足大小的空闲分区。
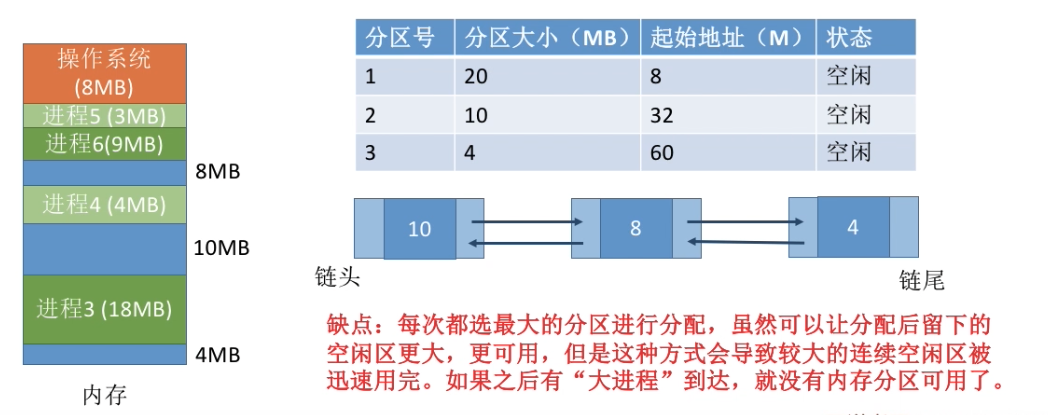
缺点:每次都选小内存的分区进行分配,会留下越来越多很小的、难以利用的内存块。因此这种方法会产生很多外部碎片
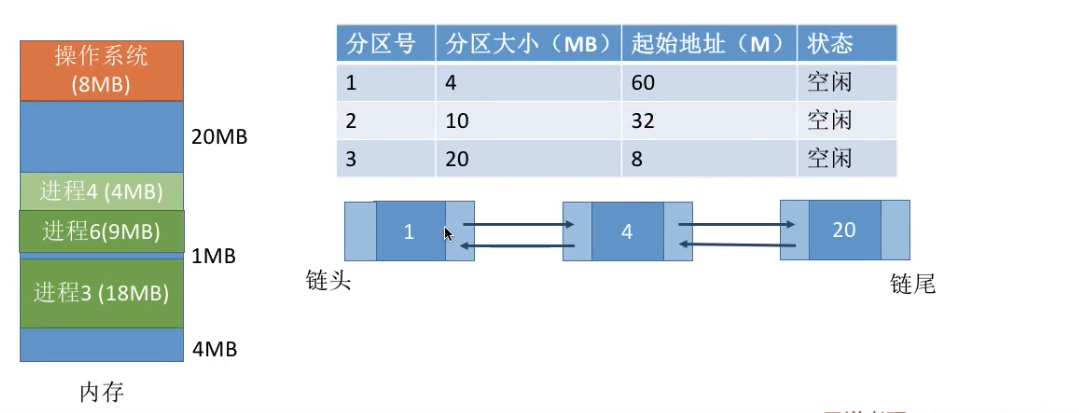
最坏适应算法(Worst Fit)
又称最大适应算法(Largest Fit)
算法思想:避免留下越来越多的小内存块,优先使用更大内存的空闲块。
实现方法:空闲分区按容量递减次序链接。每次分配内存时顺序查找空闲分区链(或空闲分区表),找到第一个满足大小的空闲分区。
缺点:导致更快是使用完大内存的空闲块,使之后的大内存的进程无分区可用
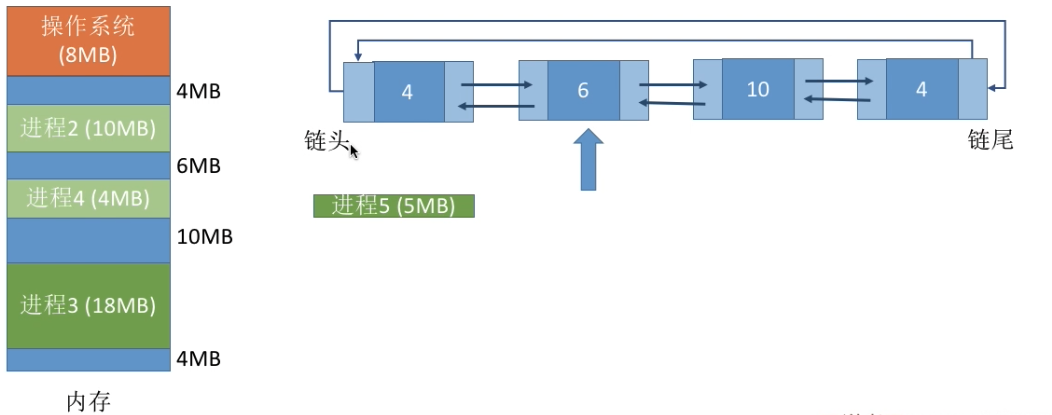
邻近适应算法(Next Fit)
算法思想:首次适应算法,每次都从低地址开始遍历,导致低地址产生越来越多很小的空闲块。新来一个进程就重新从头开始遍历,会增加查找的开销。邻近适应算法就是接着从上一次查找结束的位置开始检索。
实现方法:空闲分区按地址递增次序排列(可排成一个循环列表)。每次分配内存时从上次查找结束的位置开始查找空闲分区链(或空闲分区表),找到第一个满足大小的空闲分区。
优点:无论低地址还是高地址都有相同的概率被使用
对比
| 算法 | 算法思想 | 分区排列顺序 | 优点 |
|---|---|---|---|
| 首次适应 | 从头开始找到第一个满足大小的内存空闲分区 | 按地址递增 | 综合性能最好 算法开销小 回收分区后一般不需要对空闲分区重新排序 |
| 最佳适应 | 优先使用更小的分区 以保留更多更大的分区 |
按容量递增 | 会有更多更大的内存空闲块保留 能满足更大进程的需求 |
| 最坏适应 | 优先使用更大的分区 以防止产生太多的外部碎片 |
按容量递减 | 可以减少难以利用的小碎片(外部碎片) |
| 邻近适应 | 每次从上次结束的位置开始查找 | 按地址递增 | 不用每次从头开始检索,算法开销小 |
非连续分配管理方式
非连续分配:为用户进程分配的是一些 分散的内存空间。
假设进程A的大小为23MB,但是每个分区的大小只有10MB,如果进程只能占用一个分区,显然是放不下的。
解决思路:如果允许进程占用多个分区,那么可以把进程拆分成 10MB + 10MB + 3MB 三个部分,再把这三个部分别放在三个分区中(这些分区不要求连续)
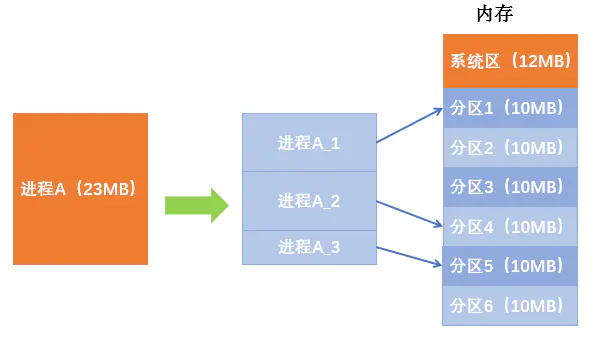
进程 A 最后的一部分只有 3MB,放入分区会产生一个 7MB 大小的内部碎片。
如果将每个分区的设为 2MB,那么进程 A 就会拆成 11 * 2MB + 1MB 共 12 个部分。最后一个部分 1MB 不会占满分区,会产生 1MB 碎片。
显然,如果把分区设置的更小一点,内部碎片会更小,内存利用率会更高。
基本分页存储管理的思想:把内存划分为一个个相等的小分区,再按照分区的大小将进程拆分成一个个小部分。
基本分页存储管理
将内存分为一个个相等的分区,每个分区就是一个页框(页框 = 页帧 = 内存块 = 物理块 = 物理页面)。
每个页框都有一个编号,即页框号(页框号 = 页帧号 = 内存块号 = 物理块号 = 物理页号),页框号从 0 开始。
将进程的逻辑地址空间分为与页框相等的一个个部分,每个部分称为一个 页 或 页面。每个页面也有一个编号,即页号,页号也从 0 开始。
操作系统 以页框为单位为各个进程分配 内存空间,进程的每个页面分别放入一个页框中(进程的页面与内存的页框有一一对应的关系)。
页框的大小不能太大,否则可能会产生过大的内存碎片。
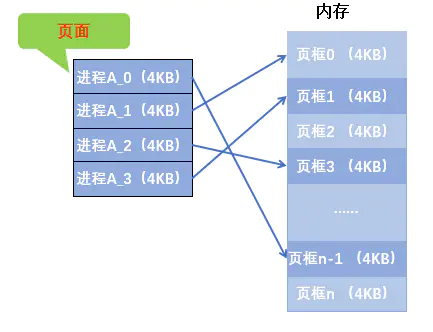
各个页面不必连续存放,也不必按先后顺序,可以放在不相邻的各个页框中。
地址转换
进程分页后,进程的各个页面可以放在不连续的页框中,所以如何实现 逻辑地址到物理的地址的转换?
如下图,将下面的进程分页,假设每页大小为50B,那么就分为4个页面。
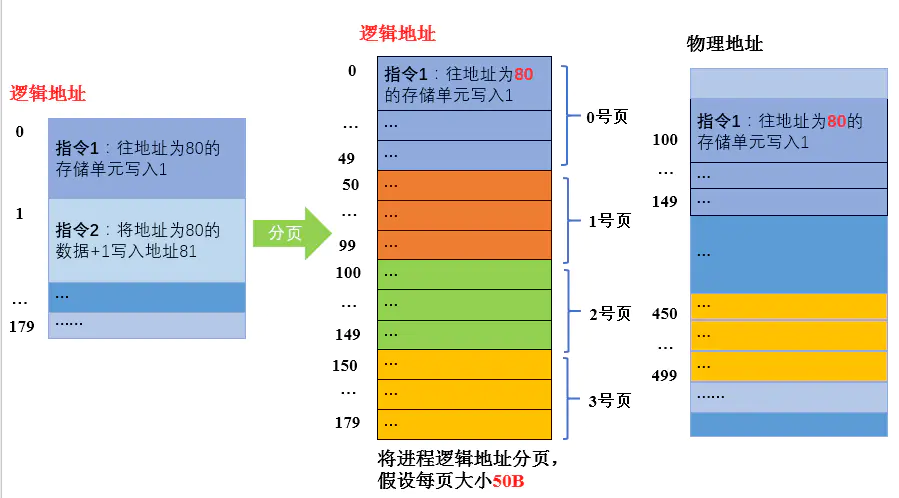
指令1需要访问逻辑地址为80的单元,逻辑地址为80的内存单元在1号页,如果1号页在内存中的物理地址为450,逻辑地址为80的内存单元相对于该页的起始地址而言,偏移量为30,所以 实际物理地址 = 450 + 30 = 480。
所以要将逻辑地址转化为实际地址需要:
- 要算出逻辑地址对应的页号。
- 要知道该页号对应的页面在内存中的起始地址。
- 计算出逻辑地址在页面内的偏移量。
- 物理地址 = 页面起始地址 + 偏移量。
手动计算方法:
- 页号 = 逻辑地址 / 页面长度(取整数部分)
- 页内偏移量 = 逻辑地址 % 页面长度
页面在内存中的起始位置:操作系统需要用某种数据结构记录进程各个页面的起始位置。
对于计算机,通常将页面的大小划分为 2 的整数次幂。假设用32个二进制位表示逻辑地址,页面大小为取212B = 4096B = 4KB。

如逻辑地址2,用二进制表示 00000000 00000000 00000000 00000010,前24位二进制对应的十进制值就是逻辑地址 2 对应的页号,即 0 号页,而后 12 二进制位对应的十进制值就是偏移量。如果 0 号页在内存中的起始地址为 X,那么逻辑地址2对应的物理地址就是 X + 2。
同理,逻辑地址 4097,用二进制表示00000000 00000000 00010000 00000001,前 24 位二进制对应的十进制值就是逻辑地址 4097 对应的页号,即 1 号页,而后 12 二进制位对应的十进制值就是偏移量。如果 0 号页在内存中的起始地址为 Y,那么逻辑地址 4097 对应的物理地址就是 Y + 1。
结论:如果每个页面的大小为 2kB,用二进制表示逻辑地址,则末尾的 K 位表示页内偏移量,其余部分就是页号。
因此,如果让每个页面的大小为 2 的整数次幂,计算机就可以很方便的得出一个逻辑地址对应的页号和页内偏移量。
如果一个页面的大小为 2KB,那分页存储管理的逻辑地址结构为:

地址结构包括两个部分:前一个部分表示页号,后一个部分表示页内偏移量 W。
页表
在知道如何计算页号和偏移量后,要计算实际的物理地址,还需要知道页号在内存中的起始地址,如何知道每个页面在内存中存放的位置——操作系统要为每个进程建立一张页表。
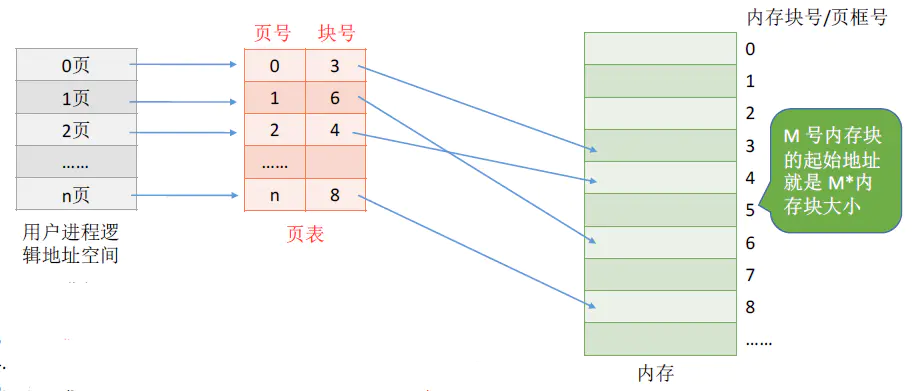
- 一个进程对应一张页表
- 进程的每一页对应一个页表项
- 每个页表项由页号和块号组成
- 页表记录进程页面和实际存放的内存块之间的对应关系
- 每个页表项的长度都是相同的,页号是隐含的(下小节)
按照之前的方法计算出逻辑地址所对应的页号N,然后根据页表区查询实际的内存块号M,由于每个内存块号的大小都是相等的,所以实际地址 = M * 内存块大小 + 偏移量。
页号隐含
在实际上,页表中是没有页号的,那怎么找到实际对应的内存块号呢?
假设某系统物理内存大小为4GB,页面大小为4KB,则每个页表项至少应该占用多少字节?
4GB = 232B,4KB = 212B。
因此 4GB 的内存一共被分为232/212 = 220个内存块,所以页表中块号的值是0~220-1。那么如果用二进制要表示最大的块号 220-1 需要 20 个二进制位,所以至少需要 3 个字节(24 个二进制位)。

各页表项会按顺序连续地存放在内存中,如果该页表在内存中存放的地址为X,则M号页对应的页表项存放的地址为:X + M * 3B
因此,页表的页号可以是隐含的。只需要知道页表存放的起始地址和页表项长度,即可找到各个页号对应的页表项存放的位置,找到位置后就可以读取该位置的值,即实际内存块号。
举个例子,如果按照逻辑地址计算出了偏移量为20,页号为1,页表中的页号是隐藏的,那么根据页表在内存中的起始地址20(假设的值),以及页表项长度3B,那么页号为1所对应的实际内存块号的值所在的地址就是:20 + 3 1 = 23的位置,然后在该位置的值,该值就是实际内存块号,如果是4的话,那么实际地址就是: 4 页面大小(4096B) + 20 = 16404。
段页式管理方式
分段
进程的地址空间:按照程序 自身的逻辑 关系 划分为若干个段,每个段都有一个段名(在低级语言中,程序员使用段名来编程),每段从 0 开始编址。
内存分配规则:以段为单位进行分配,每个段在内存中占连续空间,但 各段之间可以不相邻。
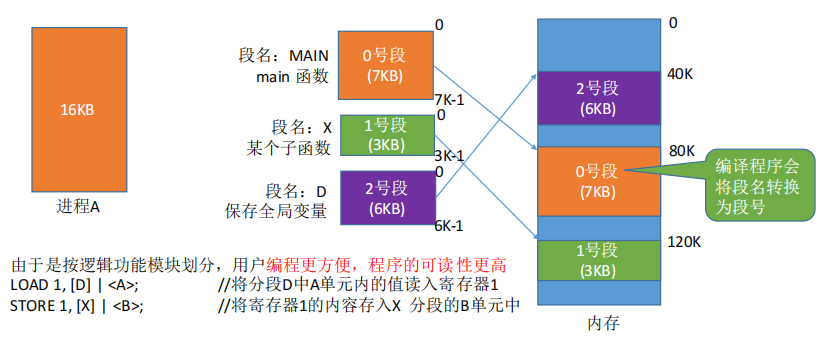
分段系统的逻辑地址结构由 段号(段名)和 段内地址(段内偏移量)所组成。

段表

每一个程序设置一个段表,放在内存,属于进程的现场信息。
地址变换
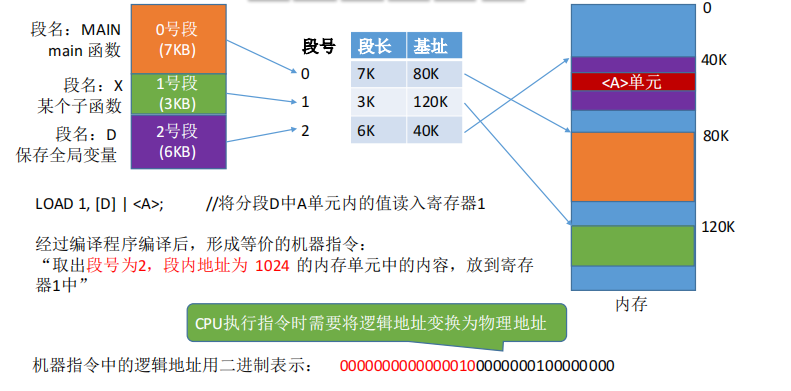
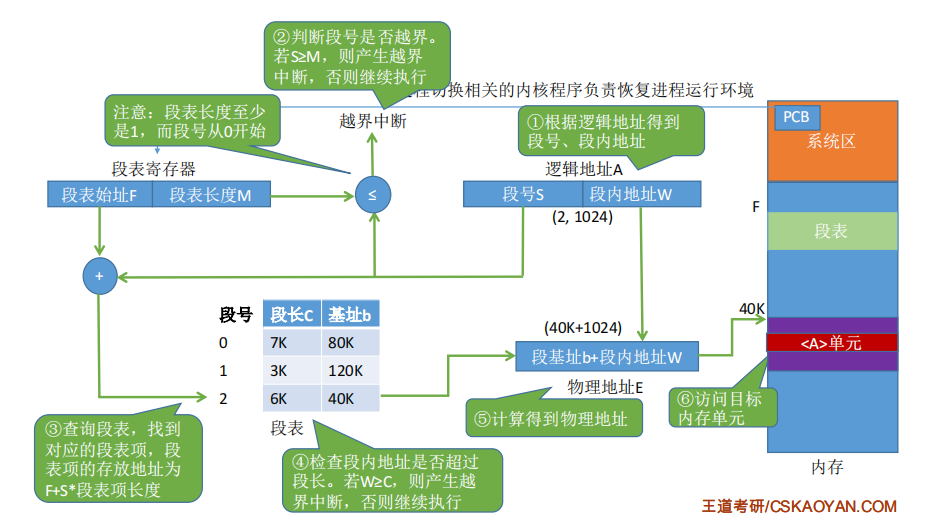
段的保护
越界中断处理
进程在执行过程中,有时需要扩大分段,如数据段。由于要访问的地址超出原有的段长,所以发越界中断。操作系统处理中断时 ,首先判断该段的“扩充位”,如可扩充,则增加段的长度;否则按出错处理。
缺段中断处理
检查内存中是否有足够的空闲空间:
① 若有,则装入该段,修改有关数据结构,中断返回
② 若没有,检查内存中空闲区的总和是否满足要求,是则应采用紧缩技术,转 ① ;否则,淘汰一(些)段,转①
段的动态连接
为何要进行段的动态链接?
大型程序由若干程序段,若干数据段组成
进程的某些程序段在进程运行期间可能根本不用
互斥执行的程序段没有必要同时驻留内存
有些程序段执行一次后不再用到
静态链接花费时间,浪费空间
在一个程序运行开始时,只将主程序段装配好并调入主存。其它各段的装配是在主程序段运行过程中逐步进行的。每当需要调用一个新段时,再将这个新段装配好,并与主程序段连接。
页式存储管理:难以完成动态链接,其逻辑地址是一维的。
信息的保护与共享
这里主要与页式存储管理进行一下对比。
分段比分页更容易实现信息的共享和保护。
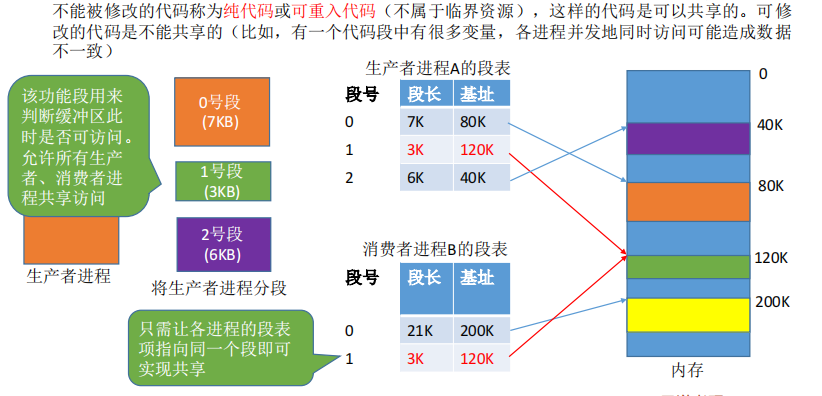
纯代码举例:比如,有一个代码段只是简单的输出“Hello World!”。
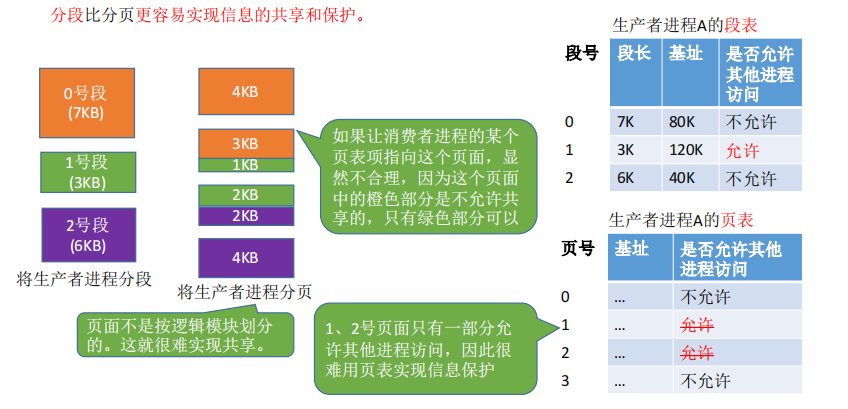
页式系统与段式系统的对比