二叉搜索树（Binary Search Tree，BST）就是为了实现快速，高效的查找，插入，删除数据而设计的。高效的原因依赖于本身的特殊结构。

特点

  • 左右子树也分别是二叉搜索树
  • 左子树的所有节点 key 值都小于它的根节点的 key 值
  • 右子树的所有节点 key 值都大于他的根节点的 key 值
  • 二叉搜索树可以为一棵空树
  • 一般来说，树中的每个节点的 key 值都不相等，但根据需要也可以将相同的 key 值插入树中

操作

插入

  • 如果为空树则将插入节点作为根节点。
  • 如果不为空树则从根节点开始，比较插入节点与根节点的 key 值，值相同则不做任何处理直接返回，大于则继续比较右子节点 R，小于则继续比较左子节点 L。
  • 右子节点 R 与插入节点比较，插入节点的 key 值大的话则继续往 R 节点的右子节点比较，小于的话则继续往R节点左子节点比较。
  • 以此类推不断往下寻找，直到找到左子节点指针或右子节点指针为空的节点，将插入节点放进去。

步骤：

  1. 创建 D 节点并与根节点比较
  2. D 小于 E，于是往左子节点继续比较
  3. D 大于 C，应该往右子节点方向，而此时 C 节点的右子节点指针为空，D 节点可以放置进去
  4. 同样的，对于 H 节点，先创建 H 节点并与根节点比较
  5. H 大于 E，于是往右子节点继续比较
  6. H 大于 G，应该往右子节点方向，而此时 G 节点的右子节点指针为空，H 节点可以放置进去

    查询

  • 从根节点开始，比较查询节点与根节点的 key 值，值相同则表示找到该节点，直接返回，大于则继续往右子节点R查找，小于则继续往左子节点L查找。
  • 右子节点R与查询节点比较，查询节点的 key 值大的话则继续往R节点的右子节点查找，小于的话则继续往R节点左子节点查找。
  • 以此类推不断往下寻找，直到找到节点的 key 值与查询节点的相同，则表示查找成功，如果最终找不到则说明不存在该节点。

步骤：

  1. B 与根节点的 key 值比较
  2. B 小于 E，往左子节点继续寻找
  3. B 小于 C，往左子节点继续寻找
  4. B 大于 A，往右子节点继续寻找，两者相等，找到
  5. 继续查询 key 值为 G 的节点，与根节点比较
  6. G 大于 E，往右子节点，两者相等，找到

    删除

    删除操作分三种情况进行：
  • 如果删除的节点为叶子节点，即它的左子节点指针和右子节点指针都为空时，则可以直接删掉该节点，并不会影响整棵树的结构。
  • 如果删除的节点只有一个子节点(左子节点或右子节点)，则直接将子节点提升到被删除的节点位置。
  • 如果删除的节点有两个子节点，此时需要找到删除节点的中序后继或中序前驱来填补删除节点，中序后继其实就是所有大于删除节点中最小的那个，而中序前驱就是所有小于删除节点中最大的那个，因为二叉搜索树经过中序遍历后是一个递增序列，所以后继就是删除节点的后面那个节点，大于且大得最少的那个，比如1 2 3 4 5中4就是3的后继。前驱就是删除节点前面那个节点，比如1 2 3 4 5中2就是3的前驱。

参考资料

Javascript代码初始化二叉树：

  1. class Node {
  2.   constructor(data) {
  3.     this.data = data
  4.     this.left = null
  5.     this.right = null
  6.   }
  7. }
  9. class BST {
  10.   constructor() {
  11.     this.root = null
  12.   }
  14.   // 插入
  15.   insert(data) {
  16.   }
  18.   // 查找
  19.   search(data) {
  20.   }
  22.   // 查找最大值
  23.   findMax() {
  24.   }
  26.   // 查找最小值
  27.   findMin() {
  28.   }
  30.   // 删除最小值
  31.   removeMin() {
  32.     if (this.root) this.root = this._removeMin(this.root)
  33.   }
  35.   // 删除最大值
  36.   removeMax() {
  37.     if (this.root) this.root = this._removeMax(this.root)
  38.   }
  40.   // 删除指定节点
  41.   remove(data) {
  42.   }
  43. }

插入：

从根节点开始，依次比较要插入的数据和节点的大小关系。 如果要插入的数据比节点的数据大，并且节点的右子树为空，就将新数据直接插到右子节点的位 置；如果不为空，就再递归遍历右子树，查找插入位置。同理，如果要插入的数据比节点数值 小，并且节点的左子树为空，就将新数据插入到左子节点的位置；如果不为空，就再递归遍历左 子树，查找插入位置。

  1. // 插入递归版本
  2.   insert(data) {
  3.     if (!this.root) return (this.root = new Node(data))
  5.     function _insert(data, node) {
  6.       if (data < node.data) {
  7.         if (!node.left) node.left = new Node(data)
  8.         else _insert(data, node.left)
  9.       } else {
  10.         if (!node.right) node.right = new Node(data)
  11.         else _insert(data, node.right)
  12.       }
  13.     }
  14.     _insert(data, this.root)
  15.   }
  18.   // 插入非递归版本
  19.   insertWhile(data) {
  20.     if (!this.root) return (this.root = new Node(data))
  22.     // 从根节点开始比较
  23.     let node = this.root
  24.     while (true) {
  25.       // 大于往右侧
  26.       if (data > node.data) {
  27.         if (!node.right) {
  28.           node.right = new Node(data)
  29.           break
  30.         }
  31.         node = node.right
  32.       }
  34.       // 小于往左侧
  35.       if (data < node.data) {
  36.         if (!node.left) {
  37.           node.left = new Node(data)
  38.           break
  39.         }
  40.         node = node.left
  41.       }
  42.     }
  43.   }

查找：

先取根节点，如果它等于我们要查找的数 据，那就返回。如果要查找的数据比根节点的值小，那就在左子树中递归查找；如果要查找的数 据比根节点的值大，那就在右子树中递归查找。

  1. // 查找：递归版本
  2.   search(data, node = this.root) {
  3.     if (!node) return null
  4.     if (node.data === data) return node
  5.     if (data > node.data) return this.search(data, node.right)
  6.     else return this.search(data, node.left)
  7.   }
  9.   //查找：非递归版本
  10.   searchWhile(data, node = this.root) {
  11.     while (node && node.data !== data) {
  12.       if (data > node.data) {
  13.         node = node.right
  14.       } else if (data < node.data) {
  15.         node = node.left
  16.       }
  17.     }
  18.     return node
  19.   }

查找搜索二叉树中的最大值、最小值：

因为在删除指定节点的时候需要用到，所以这里把_findMax，_findMin方法作为私有方法标记下。

对于以任意节点为根的二叉树，最大值永远是右子树的最右子节点。最小值永远是左子树的最左子节点。

递归代码实现：

  1. // 查找最大值
  2.   findMax() {
  3.     if (this.root) return this._findMax(this.root)
  4.   }
  6.  // 查找以某个节点为根的树的最大值
  7.   _findMax(node) {
  8.     if (!node.right) return node
  9.     return this._findMax(node.right)
  10.   }
  12.   // 查找最小值
  13.   findMin() {
  14.     if (this.root) return this._findMin(this.root)
  15.   }
  17.   // 查找以某个节点为根的树的最小值
  18.   _findMin(node) {
  19.     if (!node.left) return node
  20.     return this._findMin(node.left)
  21.   }

非递归代码实现：

  1. // 查找最大值
  2.   findMax() {
  3.     let node = this.root
  4.     while(node){
  5.       if(!node.right) break
  6.       node = node.right
  7.     }
  8.     return node
  9.   }
  11.   // 查找最小值
  12.   findMin() {
  13.     let node = this.root
  14.     while(node){
  15.       if(!node.left) break
  16.       node = node.left
  17.     }
  18.     return node
  19.   }

删除最大、最小值：

递归代码实现：

递归的思路是：每传入一个节点，删除以该节点为根的二叉树的最小值，并返回删除后的新的二叉搜索树的根。

  1. // 删除最小值
  2.   removeMin() {
  3.     if (this.root) this.root = this._removeMin(this.root)
  4.   }
  6.   // _removeMin函数是删除以node为根的二叉搜索树的最小节点
  7.   // 返回删除node最小节点后新的二分搜索树的根
  8.   _removeMin(node) {
  9.     // 如果没有左子节点，直接返回右子节点，为null一样适用
  10.     if (!node.left) return node.right
  11.     node.left = this._removeMin(node.left)
  12.     return node
  13.   }
  15.   // 删除最大值
  16.   removeMax() {
  17.     if (this.root) this.root = this._removeMax(this.root)
  18.   }
  20.   _removeMax(node) {
  21.     if (!node.right) return node.left
  22.     node.right = this._removeMax(node.right)
  23.     return node
  24.   }

非递归代码实现：

要删除最小节点，关键是找到要删除节点的父节点，然后把父节点的left（最小值）或right（最大值）指向最大值的左子节点或最小值的右子节点。

  1. removeMin() {
  2.     // 关键是找到要删除的最小值的父节点，然后让父节点 p.left = null
  3.     if(!this.root) return null
  4.     if (!this.root.left) return this.root = this.root.right
  6.     let node = this.root,
  7.       p = this.root
  8.     while (node) {
  9.       if (!node.left) break;
  10.       // p缓存父节点
  11.       p = node
  12.       node = node.left
  13.     }
  14.     p.left = node.right
  15.   }
  17.   removeMax() {
  18.     if(!this.root) return null
  19.     if(!this.root.right) return this.root = this.root.left
  21.     let node = this.root,p = this.root
  22.     while(node){
  23.       if(!node.right) break; 
  24.       // p缓存父节点
  25.       p = node
  26.       node = node.right
  27.     }
  28.     p.right = node.left
  29.   }

删除：

二叉查找树的查找、插入操作都比较简单，但删除操作就比较复杂 。针对要删除 节点的子节点个数的不同，需分三种情况来处理。

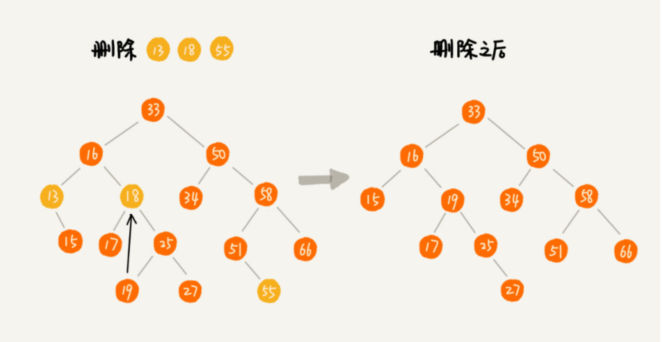
第一种情况是，如果要删除的节点没有子节点，我们只需要直接将父节点中，指向要删除节点的 指针置为 null。比如图中的删除节点 55。

第二种情况是，如果要删除的节点只有一个子节点（只有左子节点或者右子节点），我们只需要 更新父节点中，指向要删除节点的指针（可能是指向左子节点的指针，也可能是指向右子节点的指针），让它指向要删除节点的子节点就可以了。比如图中的删 除节点 13。

第三种情况是，如果要删除的节点有两个子节点，这就比较复杂了。我们需要找到这个节点的右 子树中的最小节点，把它替换到要删除的节点上。然后再删除掉这个最小节点，因为最小节点肯 定没有左子节点（如果有左子结点，那就不是最小节点了），所以，我们可以应用上面两条规则 来删除这个最小节点。比如图中的删除节点 18。

二分搜索树 - 图1

实际上，关于二叉查找树的删除操作，还有个非常简单、取巧的方法，就是单纯将要删除的节点 标记为“已删除”，但是并不真正从树中将这个节点去掉。这样原本删除的节点还需要存储在内存 中，比较浪费内存空间，但是删除操作就变得简单了很多。而且，这种处理方法也并没有增加插 入、查找操作代码实现的难度。

删除代码递归实现：

思路类似删除最大最小值，函数_remove接受一个节点node，返回值是删除指定节点后返回的新的以node为根的二叉树

  1. // 删除指定节点
  2.   remove(data) {
  3.     if (this.root) this.root = this._remove(this.root, data)
  4.   }
  6.   _remove(node, data) {
  7.     if (!node) return null
  8.     // 小于node节点
  9.     if (data < node.data) {
  10.       node.left = this._remove(node.left)
  11.       return node
  12.     } else if (data > node.data) {
  13.       node.right = this._remove(node.right)
  14.       return node
  15.     } else {
  16.       // 如果找到了指定的节点，需要根据该节点的子节点情况删除
  17.       // 如果node没有子节点也会走第一个if，node.right===null同样适合
  18.       if (!node.left) {
  19.         return node.right
  20.       } else if (!node.right) {
  21.         return node.left
  22.       } else {
  23.         // 如果自右子节点都存在，需要找到左子树中的最大子节点（前驱节点）
  24.         // 或者右子树中的最小子节点（后继节点）
  25.         // 这里找右子树中的最小子节点，successorNode叫后继节点
  26.         let successorNode = this._findMin(node.right)
  27.         // 删除右子树中的最小节点，并将返回的新二叉树返回，赋值给后继节点的右指针
  28.         successorNode.right = this._removeMin(node.right)
  29.         // 后继节点的左指针指向找到的原node节点的左指针
  30.         successorNode.left = node.left
  31.         return successorNode
  32.       }
  33.     }
  34.   }

非递归实现：
第一步：找到该节点，及该节点的父节点，并且记录下父节点的方向。
第二步：根据该节点的子节点情况进行删除

  1. remove(data) {
  2.     // 先要找到该节点，和该节点的父节点
  3.     let node = this.root,
  4.       // 记录父节点
  5.       p = this.root,
  6.       directive = null
  7.     while (node && node.data !== data) {
  8.       p = node
  9.       if (data < node.data) {
  10.         node = node.left
  11.         directive = 'left'
  12.       } else {
  13.         node = node.right
  14.         directive = 'right'
  15.       }
  16.     }
  17.     if (!node) return '没有该节点'
  18.     // 找到node后，需要根据node子节点的不同情况处理
  19.     if (!node.left) {
  20.       p[directive] = node.right
  21.     } else if (!node.right) {
  22.       p[directive] = node.left
  23.     } else {
  24.       // 如果有两个子节点
  25.       // 这里找左子树的最大值
  26.       let maxNode = node.left,
  27.         maxNodeParent = node
  28.       while (maxNode) {
  29.         if (!maxNode.right) break;
  30.         maxNodeParent = maxNode
  31.         maxNode = maxNode.right
  32.       }
  33.       // 说明要删除的node的左子节点就是我们要找的最大值
  34.       if (maxNodeParent === node) {
  35.         p[directive] = maxNode
  36.         maxNode.right = node.right
  37.       } else {
  38.         maxNodeParent.right = null
  39.         p[directive] = maxNode
  40.         maxNode.right = node.right
  41.         maxNode.left = node.left
  42.       }
  43.     }
  44.   }

二叉搜索树的遍历：

前序中序后序的本质都是深度优先，只是操作的具体位置不同而已。

前序中序后序遍历的概念已经在前面有提到。需要记得两点的是：二叉搜索树的中序遍历其实就是从小到大排序的结果。后序适合一些特殊的操作，比如树的释放，因为释放都需要先释放子节点，再释放父节点，刚好是满足的。

  1. preTraversal(node = this.root) {
  2.     if (node) {
  3.       console.log(node.data);
  4.       this.preTraversal(node.left)
  5.       this.preTraversal(node.right)
  6.     }
  7.   }
  9.   midTraversal(node=this.root) {
  10.     if(node){
  11.       this.midTraversal(node.left)
  12.       console.log(node.data);
  13.       this.midTraversal(node.right)
  14.     }
  15.   }
  17.   postTraversal(node=this.root) {
  18.     if(node){
  19.       this.postTraversal(node.left)
  20.       this.postTraversal(node.right)
  21.       console.log(node.data);
  22.     }
  23.   }

二分搜索数还有其他的操作，比如求某个数的floor，ceil？

重复二叉搜索树如何处理？

上面的操作方法都是基于二叉树中不存在健值相同的情况，如果相同的话呢？这个时候我们可能就需要把这些方法都稍作调整。

思路：

  • 对于插入的话，我们可以把相同的数据都存储在一个节点上，这样的话，我们的节点上存储的就不再是简单的数字，必须是一个对象。
  • 仍然每个节点只存储一个数据，插入的时候，如果碰到相同的值，就把这个数据插入到右子树中，就是相当于把相等的值当大于这个节点的值处理。如果要查找的话，也一样，遇到相同的节点，我们要继续在右子树中查找，直到找到所有等于这个值的节点为止。删除也是。

二叉搜索树时间复杂度：

二叉搜索树的时间复杂度的分析其实跟我们在快排排序的分析很类似，都是类似的递归树的分析，如果二叉树根节点的左右子树不平衡，就会影响到时间复杂度的计算，最差情况退化为链表，时间复杂度变成O(n)。满二叉树、完全二叉树就是O(logn)。其实时间复杂度就是跟树的高度成正比。所以在实际应用中，这也是平衡二叉树会比较受欢迎的原因。

完整代码：

  1. class Node {
  2.   constructor(data) {
  3.     this.data = data
  4.     this.left = null
  5.     this.right = null
  6.   }
  7. }
  9. class BST {
  10.   constructor() {
  11.     this.root = null
  12.   }
  14.   // 插入递归版本
  15.   insert(data) {
  16.     if (!this.root) return (this.root = new Node(data))
  18.     function _insert(data, node) {
  19.       if (data < node.data) {
  20.         if (!node.left) node.left = new Node(data)
  21.         else _insert(data, node.left)
  22.       } else {
  23.         if (!node.right) node.right = new Node(data)
  24.         else _insert(data, node.right)
  25.       }
  26.     }
  27.     _insert(data, this.root)
  28.   }
  30.   // 插入非递归版本
  31.   insertWhile(data) {
  32.     if (!this.root) return (this.root = new Node(data))
  34.     // 从根节点开始比较
  35.     let node = this.root
  36.     while (true) {
  37.       // 大于往右侧
  38.       if (data > node.data) {
  39.         if (!node.right) {
  40.           node.right = new Node(data)
  41.           break
  42.         }
  43.         node = node.right
  44.       }
  46.       // 小于往左侧
  47.       if (data < node.data) {
  48.         if (!node.left) {
  49.           node.left = new Node(data)
  50.           break
  51.         }
  52.         node = node.left
  53.       }
  54.     }
  55.   }
  57.   // 查找：递归版本
  58.   search(data, node = this.root) {
  59.     if (!node) return null
  60.     if (node.data === data) return node
  61.     if (data > node.data) return this.search(data, node.right)
  62.     else return this.search(data, node.left)
  63.   }
  65.   //查找：非递归版本
  66.   searchWhile(data, node = this.root) {
  67.     while (node && node.data !== data) {
  68.       if (data > node.data) {
  69.         node = node.right
  70.       } else if (data < node.data) {
  71.         node = node.left
  72.       }
  73.     }
  74.     return node
  75.   }
  77.   // 查找最大值
  78.   findMax() {
  79.     if (this.root) return this._findMax(this.root)
  80.   }
  82.   _findMax(node) {
  83.     if (!node.right) return node
  84.     return this._findMax(node.right)
  85.   }
  87.   // 查找最小值
  88.   findMin() {
  89.     if (this.root) return this._findMin(this.root)
  90.   }
  92.   _findMin(node) {
  93.     if (!node.left) return node
  94.     return this._findMin(node.left)
  95.   }
  97.   // 删除最小值
  98.   removeMin() {
  99.     if (this.root) this.root = this._removeMin(this.root)
  100.   }
  102.   // _removeMin函数是删除以node为根的二叉搜索树的最小节点
  103.   // 返回删除node最小节点后新的二分搜索树的根
  104.   _removeMin(node) {
  105.     // 如果没有左子节点，直接返回右子节点，为null一样适用
  106.     if (!node.left) return node.right
  107.     node.left = this._removeMin(node.left)
  108.     return node
  109.   }
  111.   // 删除最大值
  112.   removeMax() {
  113.     if (this.root) this.root = this._removeMax(this.root)
  114.   }
  116.   _removeMax(node) {
  117.     if (!node.right) return node.left
  118.     node.right = this._removeMax(node.right)
  119.     return node
  120.   }
  122.   // 删除指定节点
  123.   remove(data) {
  124.     if (this.root) this.root = this._remove(this.root, data)
  125.   }
  127.   _remove(node, data) {
  128.     if (!node) return null
  129.     // 小于node节点
  130.     if (data < node.data) {
  131.       node.left = this._remove(node.left)
  132.       return node
  133.     } else if (data > node.data) {
  134.       node.right = this._remove(node.right)
  135.       return node
  136.     } else {
  137.       // 如果找到了指定的节点，需要根据该节点的子节点情况删除
  138.       if (!node.left) {
  139.         return node.right
  140.       } else if (!node.right) {
  141.         return node.left
  142.       } else {
  143.         // 如果自右子节点都存在，需要找到左子树中的最大子节点（前驱节点）
  144.         // 或者右子树中的最小子节点（后继节点）
  145.         // 这里找右子树中的最小子节点，successorNode叫后继节点
  146.         let successorNode = this._findMin(node.right)
  147.         // 删除右子树中的最小节点，并将返回的新二叉树返回，赋值给后继节点的右指针
  148.         successorNode.right = this._removeMin(node.right)
  149.         // 后继节点的左指针指向找到的原node节点的左指针
  150.         successorNode.left = node.left
  151.         return successorNode
  152.       }
  153.     }
  154.   }
  155. }
  157. let bst = new BST()
  159. bst.insertWhile(34)
  160. bst.insertWhile(32)
  161. bst.insertWhile(56)
  162. bst.insertWhile(43)
  163. bst.insertWhile(51)
  164. bst.insertWhile(45)
  165. bst.insertWhile(25)
  166. bst.insertWhile(67)
  167. bst.insertWhile(40)
  168. bst.insertWhile(39)
  169. bst.insertWhile(33)
  171. console.log(bst)
  172. console.log(bst.search(10))
  174. console.log(bst.findMin())
  175. console.log(bst.findMax())
  177. // 删除最大、最小值
  178. bst.removeMin()
  179. bst.removeMax()
  180. console.log(bst)
  182. // 删除指定节点
  183. bst.remove(56)
  184. console.log(bst)