title: 时间复杂度和空间复杂度
date: 2019-03-12 22:07:29
categories: 代码
tags: 算法学习

why?

前言

衡量代码的好坏包括两个重要的指标

  1. 运行时间
  2. 占用空间

基本操作执行次数
关于代码的基本操作执行次数，我们用四个生活中的场景，来做一下比喻：

场景1 ：给小灰一条长10寸的面包，小灰每3天吃掉1寸，那么吃掉整个面包需要几天？

答案自然是 3 X 10 = 30天。
如果面包的长度是 N 寸呢？
此时吃掉整个面包，需要 3 X n = 3n 天。
如果用一个函数来表达这个相对时间，可以记作 T（n） = 3n。

场景2：给小灰一条长16寸的面包，小灰每5天吃掉面包剩余长度的一半，第一次吃掉8寸，第二次吃掉4寸，第三次吃掉2寸……那么小灰把面包吃得只剩下1寸，需要多少天呢？

这个问题翻译一下，就是数字16不断地除以2，除几次以后的结果等于1？这里要涉及到数学当中的对数，以2位底，16的对数，可以简写为log16。
因此，把面包吃得只剩下1寸，需要 5 X log16 = 5 X 4 = 20 天。
如果面包的长度是 N 寸呢？
需要 5 X logn = 5logn天，记作 T（n） = 5logn。

场景3: 给小灰一条长10寸的面包和一个鸡腿，小灰每2天吃掉一个鸡腿。那么小灰吃掉整个鸡腿需要多少天呢？

答案自然是2天。因为只说是吃掉鸡腿，和10寸的面包没有关系 。
如果面包的长度是 N 寸呢？
无论面包有多长，吃掉鸡腿的时间仍然是2天，记作 T（n） = 2。

场景4: 给小灰一条长10寸的面包，小灰吃掉第一个一寸需要1天时间，吃掉第二个一寸需要2天时间，吃掉第三个一寸需要3天时间…..每多吃一寸，所花的时间也多一天。那么小灰吃掉整个面包需要多少天呢？

答案是从1累加到10的总和，也就是55天。
如果面包的长度是 N 寸呢？
此时吃掉整个面包，需要 1+2+3+……+ n-1 + n = (1+n)*n/2 = 0.5n^2 + 0.5n。
记作 T（n） = 0.5n^2 + 0.5n。

时间复杂度

表示法

若存在函数f(n),使得n趋近于无穷大时，T(n)/f(n) 的极限值为不等于零的常熟，则称f(n)是T(n)的同数量级函数。记作T(n) = O( f(n) )为算法的渐进复杂度，简称时间复杂度。渐进时间复杂度用大写O来表示，所以也被称为大O表示法。

场景1：
T（n） = 3n
最高阶项为3n，省去系数3，转化的时间复杂度为：
T（n） = O（n）
{% asset_img O(n).jpg O(n) %}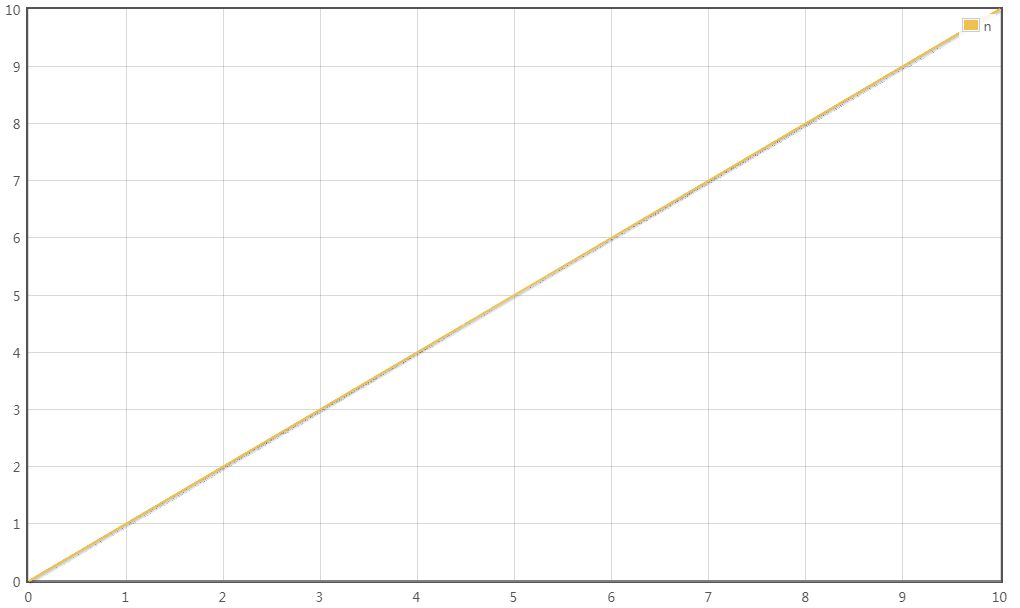
O(n).jpg

场景2：
T（n） = 5logn
最高阶项为5logn，省去系数5，转化的时间复杂度为：
T（n） = O（logn）
{% asset_img O(logn).png O(logn) %}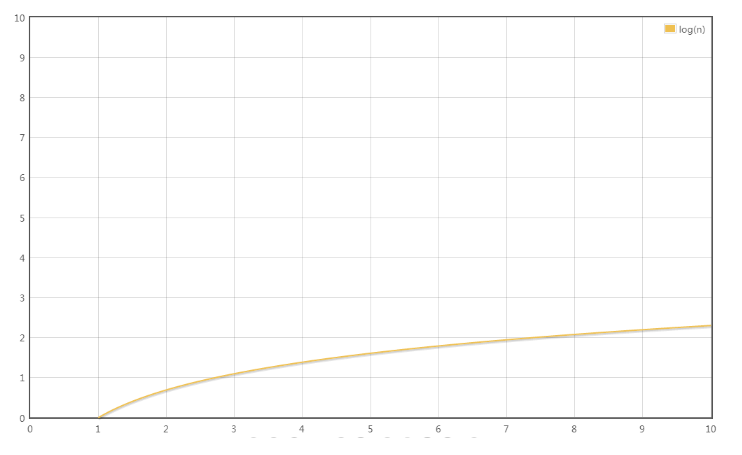
O(logn).png

场景3：
T（n） = 2
只有常数量级，转化的时间复杂度为：
T（n） = O（1）
{% asset_img O(1).png O(1) %}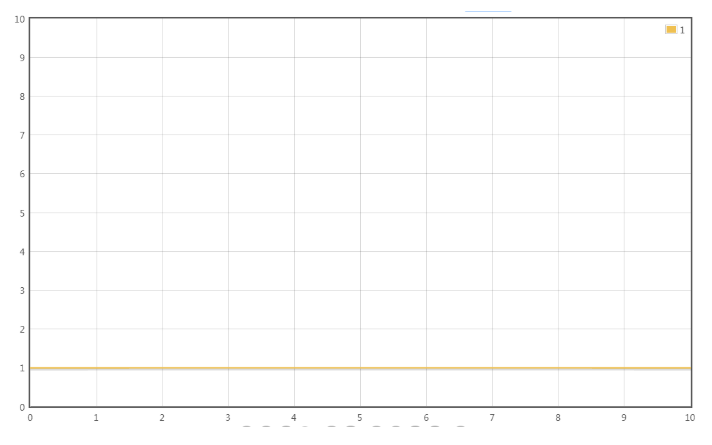
O(1).png

场景4：
T（n） = 0.5n^2 + 0.5n
最高阶项为0.5n^2，省去系数0.5，转化的时间复杂度为：
T（n） = O（n^2）
{% asset_img O(n^2).png O(n^2) %}

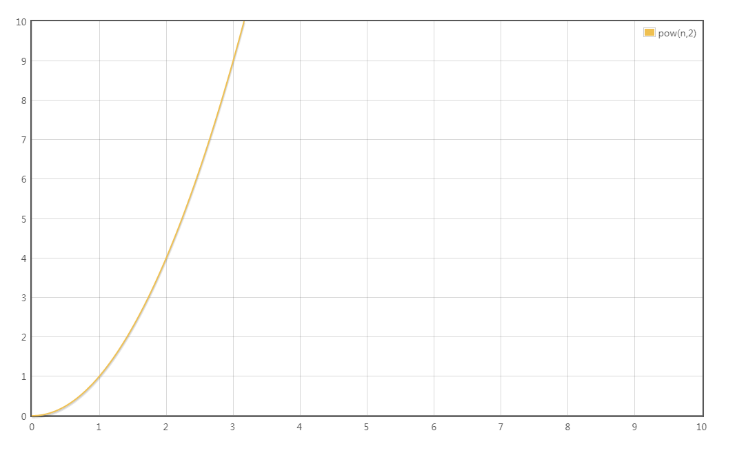
O(n^2).png
这四种时间复杂度究竟谁用时更长，谁节省时间呢？稍微思考一下就可以得出结论：
O（1）< O（logn）< O（n）< O（n^2）
在编程的世界中有着各种各样的算法，除了上述的四个场景，还有许多不同形式的时间复杂度，比如：
O（nlogn）, O（n^3）, O（m*n），O（2^n），O（n！）

代码分析

由此可见，由执行次数 T(n) 得到时间复杂度并不困难，很多时候困难的是从算法通过分析和数学运算得到 T(n)。对此，提供下列四个便利的法则，这些法则都是可以简单推导出来的，总结出来以便提高效率。

  1. 对于一个循环，假设循环体的时间复杂度为 O(n)，循环次数为 m，则这个
    循环的时间复杂度为 O(n×m)。
  1. void aFunc(int n) {
  2.     for(int i = 0; i < n; i++) {         // 循环次数为 n
  3.         printf("Hello, World!\n");      // 循环体时间复杂度为 O(1)
  4.     }
  5. }

此时时间复杂度为 O(n × 1)，即 O(n)。

  1. 对于多个循环，假设循环体的时间复杂度为 O(n)，各个循环的循环次数分别是a, b, c…，则这个循环的时间复杂度为 O(n×a×b×c…)。分析的时候应该由里向外分析这些循环。
  1. void aFunc(int n) {
  2.     for(int i = 0; i < n; i++) {         // 循环次数为 n
  3.         for(int j = 0; j < n; j++) {       // 循环次数为 n
  4.             printf("Hello, World!\n");      // 循环体时间复杂度为 O(1)
  5.         }
  6.     }
  7. }

此时时间复杂度为 O(n × n × 1)，即 O(n^2)。

  1. 对于顺序执行的语句或者算法，总的时间复杂度等于其中最大的时间复杂度。
  1. void aFunc(int n) {
  2.     // 第一部分时间复杂度为 O(n^2)
  3.     for(int i = 0; i < n; i++) {
  4.         for(int j = 0; j < n; j++) {
  5.             printf("Hello, World!\n");
  6.         }
  7.     }
  8.     // 第二部分时间复杂度为 O(n)
  9.     for(int j = 0; j < n; j++) {
  10.         printf("Hello, World!\n");
  11.     }
  12. }

此时时间复杂度为 max(O(n^2), O(n))，即 O(n^2)。

  1. 对于条件判断语句，总的时间复杂度等于其中 时间复杂度最大的路径 的时间复杂度。
  1. void aFunc(int n) {
  2.     if (n >= 0) {
  3.         // 第一条路径时间复杂度为 O(n^2)
  4.         for(int i = 0; i < n; i++) {
  5.             for(int j = 0; j < n; j++) {
  6.                 printf("输入数据大于等于零\n");
  7.             }
  8.         }
  9.     } else {
  10.         // 第二条路径时间复杂度为 O(n)
  11.         for(int j = 0; j < n; j++) {
  12.             printf("输入数据小于零\n");
  13.         }
  14.     }
  15. }

此时时间复杂度为 max(O(n^2), O(n))，即 O(n^2)。

时间复杂度分析的基本策略是：从内向外分析，从最深层开始分析。如果遇到函数调用，要深入函数进行分析。

附1

求该方法的时间复杂度

  1. void aFunc(int n) {
  2.     for (int i = 2; i < n; i++) {
  3.         i *= 2;
  4.         printf("%i\n", i);
  5.     }
  6. }

假设循环次数为 t，则循环条件满足 2^t < n。
可以得出，执行次数t = log(2)(n)，即 T(n) = log(2)(n)，可见时间复杂度为 O(log(2)(n))，即 O(log n)。

附2

求该方法的时间复杂度

  1. long aFunc(int n) {
  2.     if (n <= 1) {
  3.         return 1;
  4.     } else {
  5.         return aFunc(n - 1) + aFunc(n - 2);
  6.     }
  7. }

参考答案：
显然运行次数，T(0) = T(1) = 1，同时 T(n) = T(n - 1) + T(n - 2) + 1，这里的 1 是其中的加法算一次执行。
显然 T(n) = T(n - 1) + T(n - 2) 是一个斐波那契数列，通过归纳证明法可以证明，当 n >= 1 时 T(n) < (5/3)^n，同时当 n > 4 时 T(n) >= (3/2)^n。
所以该方法的时间复杂度可以表示为 O((5/3)^n)，简化后为 O(2^n)。
可见这个方法所需的运行时间是以指数的速度增长的。如果大家感兴趣，可以试下分别用 1，10，100 的输入大小来测试下算法的运行时间，相信大家会感受到时间复杂度的无穷魅力。

空间复杂度

待补