title: 递归
date: 2019-03-13 23:44:00
categories: 代码
tags: 算法学习
mathjax: true

递归从入门到精通

递归入门

编写一个递归函数

• 这个递归函数的功能是什么，怎样调用这个函数，即设计好递归函数的返回值和参数列表
• 什么时候应该结束这个递归，它的边界条件（出口）是什么 （边界条件）
• 在非边界情况时，怎样从第n层转变成第n+1层 (递推公式)

计算阶乘(factorial)

!%20%26%20n%3E0%0A%5Cend%7Bcases%7D%0A#card=math&code=%0An%21%3D%5Cbegin%7Bcases%7D%0A1%20%26%20n%3D0%20%5C%5C%0An%2A%28n-1%29%21%20%26%20n%3E0%0A%5Cend%7Bcases%7D%0A&id=mQs4R)

int fact(int n){
    if (n == 0) return 1;
    return n * fact(n - 1);
}
int ans = fact(10); //调用（递归）函数

计算最大公约数(辗转相除法)

gcd(12, 32) = 4
gcd(a,   b)
gcd(32,  12)
gcd(12,  8)
gcd(8,   4)
gcd(4,   0)

%3D%5Cbegin%7Bcases%7D%0Aa%20%26%20b%3D0%20%5C%5C%0Agcd(b%2Ca%20%5C%25%20b)%20%26%20b%5Cneq%200%0A%5Cend%7Bcases%7D%0A#card=math&code=%0Agcd%28a%2Cb%29%3D%5Cbegin%7Bcases%7D%0Aa%20%26%20b%3D0%20%5C%5C%0Agcd%28b%2Ca%20%5C%25%20b%29%20%26%20b%5Cneq%200%0A%5Cend%7Bcases%7D%0A&id=BLBUt)

int gcd(int a, int b){
    if (b == 0) return a;
    return gcd(b, a % b);
}
int ans = gcd(12, 32);

分治算法

分治法的设计思想：

1. 分–将问题分解为规模更小的子问题；
2. 治–将这些规模更小的子问题逐个击破；
3. 合–将已解决的子问题合并，最终得出“母”问题的解；

• 减而治之（每次让问题的规模减1）
• 分而治之（每次让问题的规模减半）（归并排序的思想）

例题：走楼梯

题目描述：
一个台阶总共有n级，如果一次可以跳1级，也可以跳2级。求总共有多少总跳法。
第一行输入T，表示有多少个测试数据。接下来T行，每行输入一个数n，表示台阶的阶数。
输出时每一行对应一个输出。
样例输入：
3
5
8
10
样例输出：
8
34
89

解析：

%3D%5Cbegin%7Bcases%7D%0A1%20%26%20n%3D1%20%5C%5C%0A2%20%26%20n%3D2%20%5C%5C%0Af(n-1)%2Bf(n-2)%20%26%20n%3E2%0A%5Cend%7Bcases%7D%0A#card=math&code=%0Af%28n%29%3D%5Cbegin%7Bcases%7D%0A1%20%26%20n%3D1%20%5C%5C%0A2%20%26%20n%3D2%20%5C%5C%0Af%28n-1%29%2Bf%28n-2%29%20%26%20n%3E2%0A%5Cend%7Bcases%7D%0A&id=UWn9A)

参考代码：

#include <stdio.h>
int solve(int n) {
    if (n == 1) return 1;
    if (n == 2) return 2;
    return solve(n - 1) + solve(n - 2);
}
int main() {
    int T;
    scanf("%d", &T);
    while (T--) {
        int n;
        scanf("%d", &n);
        int ans = solve(n);
        printf("%d\n", ans);
    }
    return 0;
}

归并排序

{% asset_img 图02-19.归并排序实例.png 归并排序实例 %}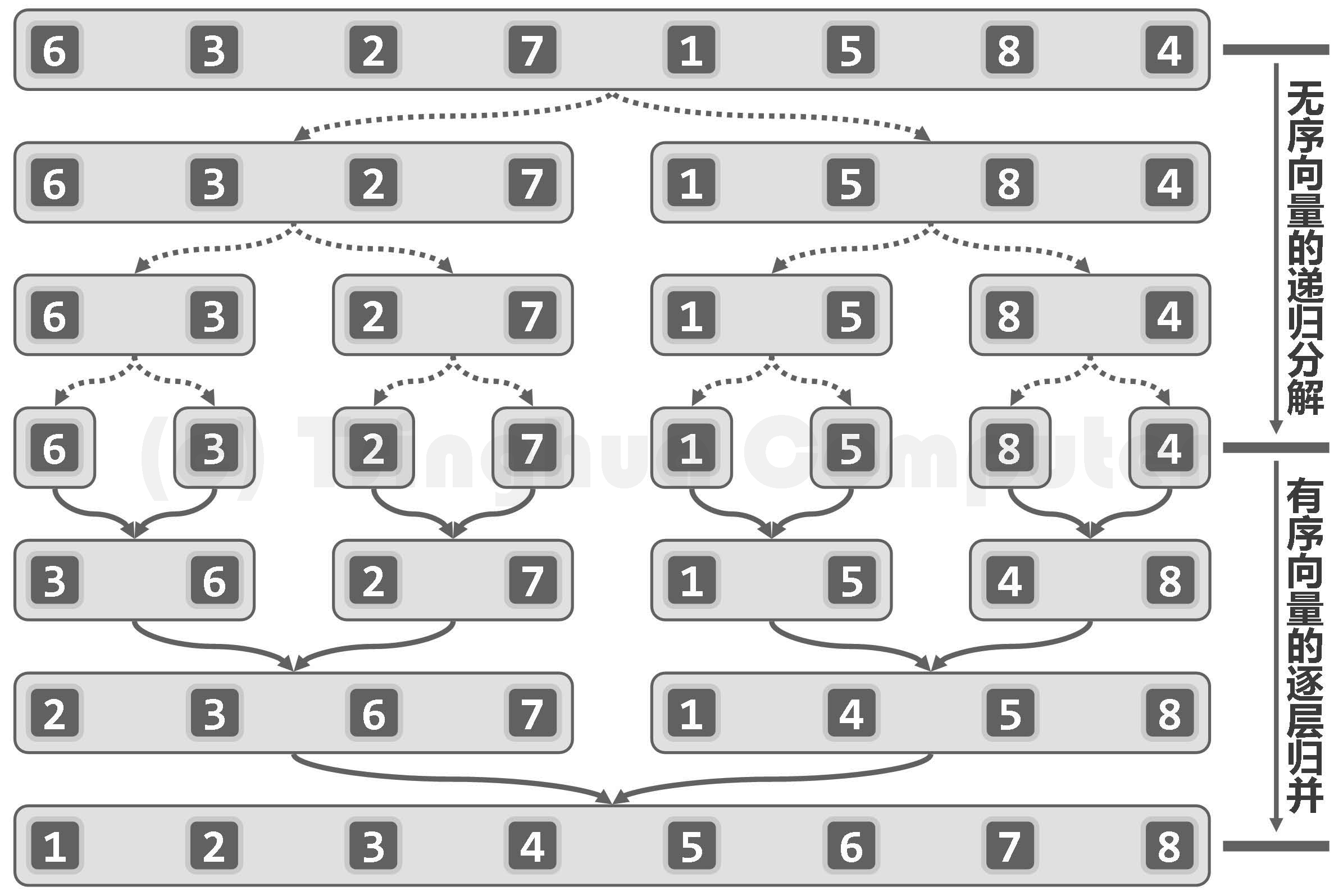

void mergeSort(int A[], int lo, int hi) {
    if (lo >= hi) return;
    int mid = lo + (hi - lo) / 2;
    mergeSort(A, lo, mid);    //左半区间[lo, mid] 排好序
    mergeSort(A, mid + 1, hi);    //右半区间[mid + 1, hi] 排好序
    mergeArray(A, lo, mid, hi);    //进行合并
}

{% asset_img 图02-18.有序向量的二路归并实例.png 有序向量的二路归并 %}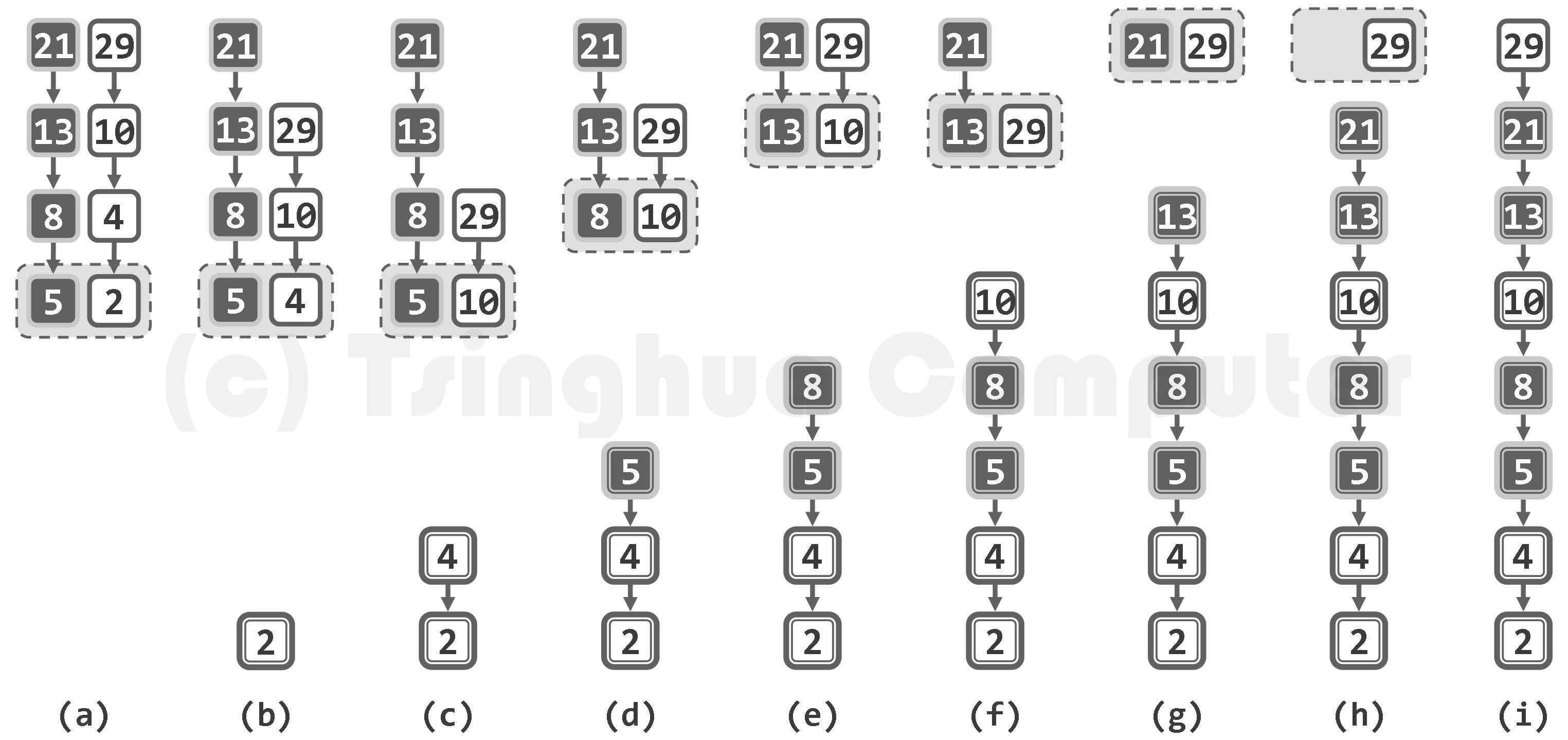

#include <iostream>
using namespace std;
void mergeArray(int A[], int lo, int mid, int hi) {
    int* temp = new int[hi - lo + 1];
    int i = lo, j = mid + 1;
    int k = 0;
    while (i <= mid && j <= hi) {
        if (A[i] <= A[j]) temp[k++] = A[i++];
        else temp[k++] = A[j++];
    }
    while (i <= mid) temp[k++] = A[i++];
    while (j <= hi) temp[k++] = A[j++];
    for (int i = lo, k = 0; i <= hi; i++, k++) {
        A[i] = temp[k];
    }
    delete[] temp;
}
void mergeSort(int A[], int lo, int hi) {
    if (lo >= hi) return;
    int mid = lo + (hi - lo) / 2;
    mergeSort(A, lo, mid);    //左半区间[lo, mid] 排好序
    mergeSort(A, mid + 1, hi);    //右半区间[mid + 1, hi] 排好序
    mergeArray(A, lo, mid, hi);    //进行合并
}
int main() {
    int A[] = { 6, 1, 2, 9, 7, 3 };
    int N = sizeof(A) / sizeof(int);
    mergeSort(A, 0, N - 1);
    for (int x : A) {
        cout << x << " ";
    }
    cout << endl;
    return 0;
}

二叉树、树

二叉树的遍历

struct Node {    //C++版本
    int data;
    Node *lchild, *rchild;
    Node(int x = 0) { data = x; lchild = rchild = NULL; }
};

先序遍历

{% asset_img 图05-28.二叉树先序遍历序列-1549953653371.png 二叉树先序遍历序列 %}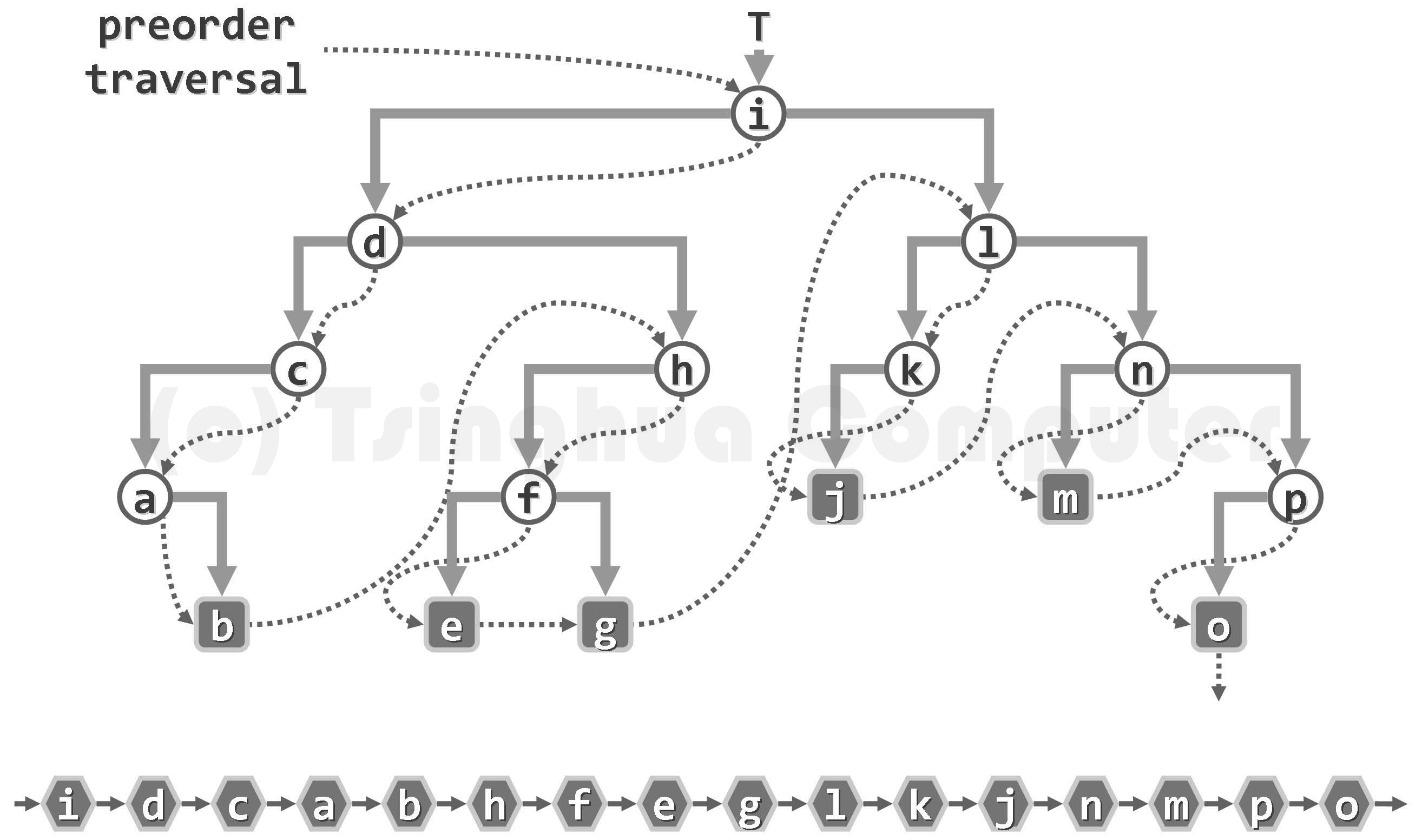

void preorderTrav(Node* root) {    //先序遍历
    if (root == NULL) return;
    printf("%d ", root->data);    //最先访问根节点
    preorderTrav(root->lchild);
    preorderTrav(root->rchild);
}
void preorderTrav(Node* root) {    //写法2
    if (root != NULL) {
        printf("%d ", root->data);
        preorderTrav(root->lchild);
        preorderTrav(root->rchild);
    }
}
void preorderTrav(Node* root) {    //写法3
    //if (root == NULL) return;    //只要能保证这棵树不是空树，这行代码就可以省略
    printf("%d ", root->data);
    if (root->lchild != NULL) {
        preorderTrav(root->lchild);
    }
    if (root->rchild != NULL) {
        preorderTrav(root->rchild);
    }
}

中序遍历

{% asset_img 图05-30.二叉树的中序遍历序列.png 二叉树的中序遍历序列 %}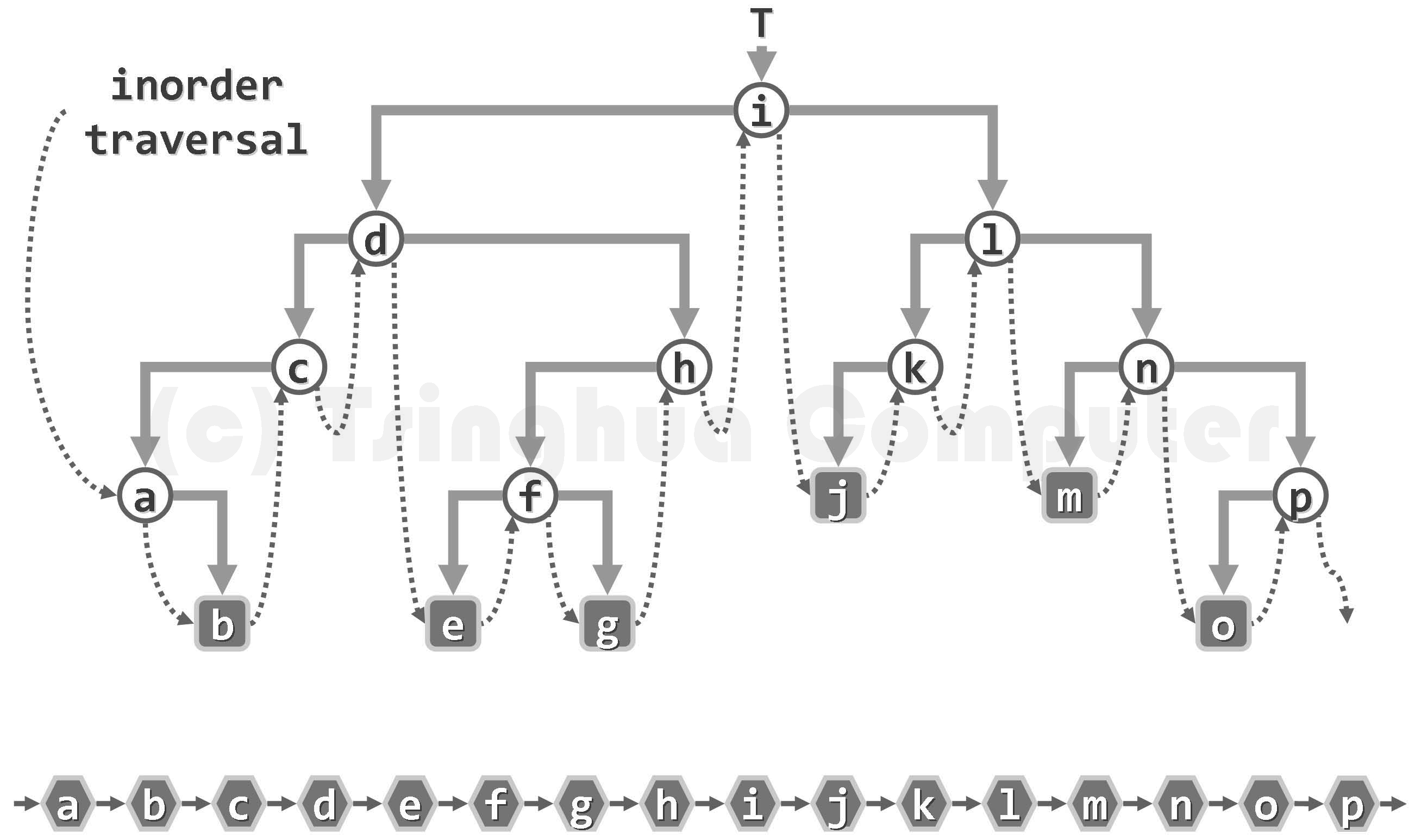

void inorderTrav(Node* root) {    //中序遍历
    if (root == NULL) return;
    inorderTrav(root->lchild);
    printf("%d ", root->data);    //中间的时候访问根节点
    inorderTrav(root->rchild);
}

二叉树节点在水平方向上的投影顺序即为中序遍历的顺序。

后序遍历

{% asset_img 图05-29.二叉树的后序遍历序列.png 二叉树的后序遍历序列 %}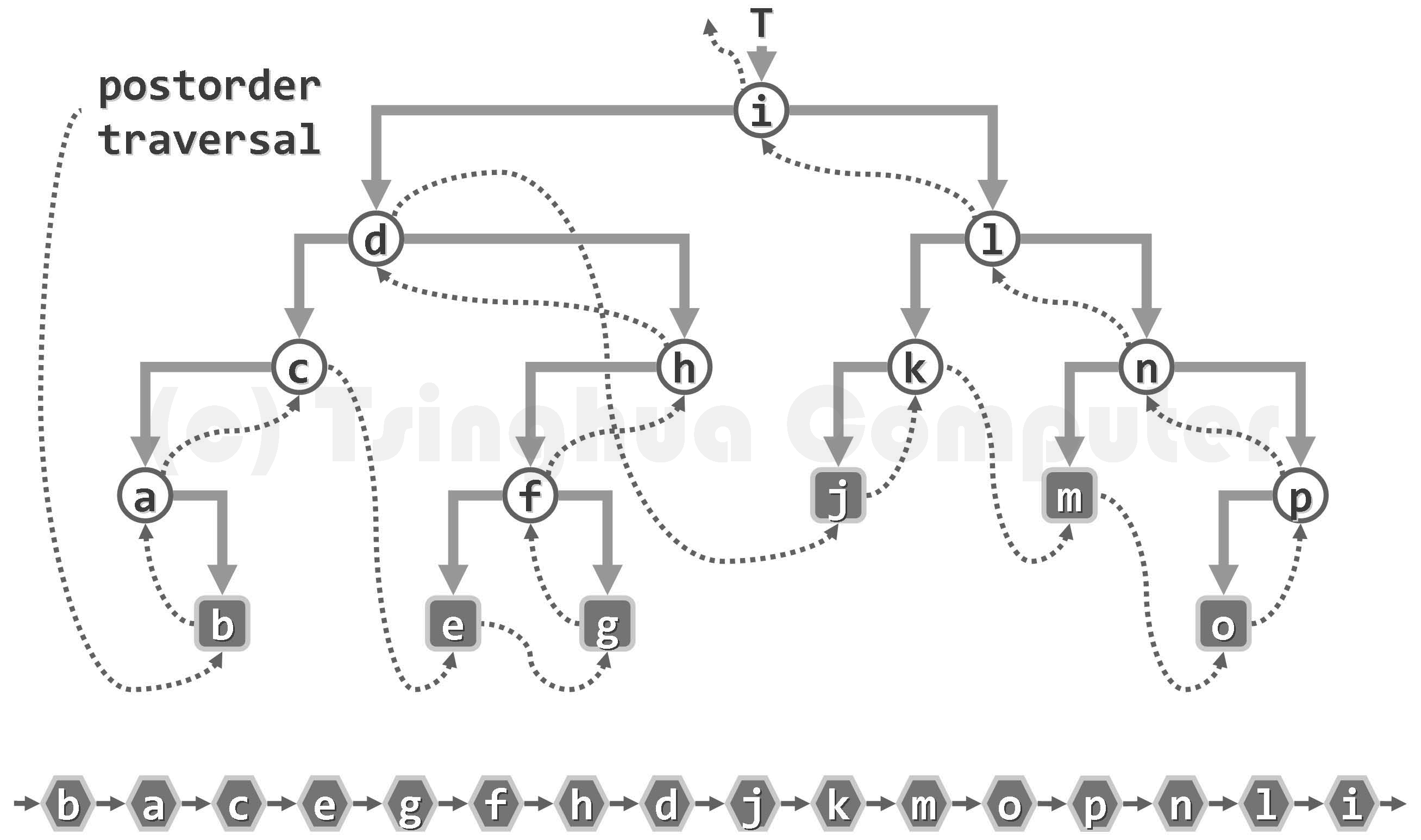

void postorderTrav(Node* root) {    //后序遍历
    if (root == NULL) return;
    postorderTrav(root->lchild);
    postorderTrav(root->rchild);
    printf("%d ", root->data);    //最后访问根节点
}

求二叉树的高度

int getTreeHigh(Node* root) {
    if (root == NULL) return 0;
    int left_high = getTreeHigh(root->lchild);
    int right_high = getTreeHigh(root->rchild);
    return max(left_high, right_high) + 1;
}

完整实现代码

#include <iostream>
#include <algorithm>
using namespace std;
struct Node {
    int data;
    Node *lchild, *rchild;
    Node(int x = 0) { data = x; lchild = rchild = NULL; }
    void setChildNode(Node* l, Node* r) {
        lchild = l;
        rchild = r;
    }
};
void preorderTrav(Node* root) {    //先序遍历
    if (root == NULL) return;
    printf("%d ", root->data);    //最先访问根节点
    preorderTrav(root->lchild);
    preorderTrav(root->rchild);
}
void inorderTrav(Node* root) {    //中序遍历
    if (root == NULL) return;
    inorderTrav(root->lchild);
    printf("%d ", root->data);    //中间的时候访问根节点
    inorderTrav(root->rchild);
}
void postorderTrav(Node* root) {    //后序遍历
    if (root == NULL) return;
    postorderTrav(root->lchild);
    postorderTrav(root->rchild);
    printf("%d ", root->data);    //最后访问根节点
}
int getTreeHeight(Node* root) {
    if (root == NULL) return 0;
    int left_high = getTreeHeight(root->lchild);
    int right_high = getTreeHeight(root->rchild);
    return max(left_high, right_high) + 1;
}
int main() {
    //完全可以用一个 Node* nodes[100] 数组来存放这些节点
    Node* root = new Node(1);
    Node* node_2 = new Node(2);
    Node* node_3 = new Node(3);
    Node* node_4 = new Node(4);
    Node* node_5 = new Node(5);
    Node* node_6 = new Node(6);
    Node* node_7 = new Node(7);
    //Node* node_8 = new Node(8);
    //root->lchild = node_2;
    //root->rchild = node_3;
    root->setChildNode(node_2, node_3);
    node_2->setChildNode(node_4, node_5);
    node_3->setChildNode(NULL, node_7);
    node_5->setChildNode(node_6, NULL);
    node_4->rchild = new Node(8);
    preorderTrav(root);
    printf("\n");
    inorderTrav(root);
    printf("\n");
    postorderTrav(root);
    printf("\n");
    printf("Tree Height: %d\n", getTreeHeight(root));
    return 0;
}

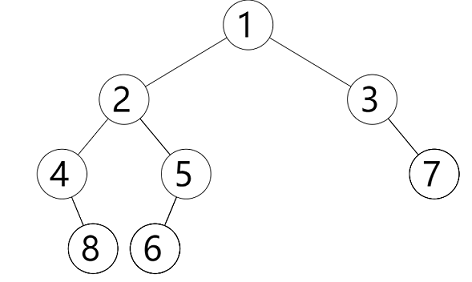
表达式树的输出与求值

表达式树的特征：叶节点是运算数，非叶节点一定是运算符

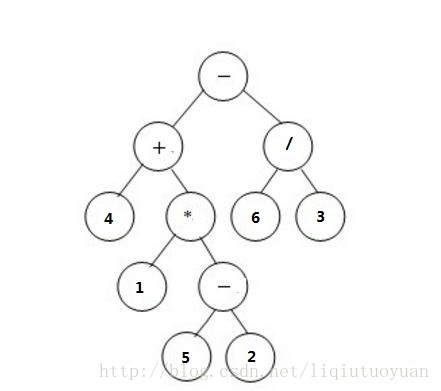
输入格式：

第一行给出节点的个数N，每个节点的编号为0 ~ N-1

接下来N行每行分别给出：

     该节点的编号、该节点的操作数/操作符、该节点的左孩子编号、右孩子编号（-1表示NULL）

输出格式：

第一行输出该表达式树的中缀表达式，该用括号的地方需要用括号括起来。

第二行输出该表达式树的前缀表达式。

第二行输出该表达式树的后缀表达式。

第四行输出该表达式树的计算结果，保留两位小数。

样例输入：

11
0 - 1 2
1 + 3 4
2 / 5 6
3 4 -1 -1
4 * 7 8
5 6 -1 -1
6 3 -1 -1
7 1 -1 -1
8 - 9 10
9 5 -1 -1
10 2 -1 -1

样例输出：

(4+(1*(5-2)))-(6/3)
- + 4 * 1 - 5 2 / 6 3
4 1 5 2 - * + 6 3 / -
5.00

完整代码：

#include <iostream>
using namespace std;

struct Node {
    char data;
    Node *lchild, *rchild;
};

void preOrder(Node* root) {                //前缀表达式
    if (root == NULL) return;
    printf("%c ", root->data);
    preOrder(root->lchild);
    preOrder(root->rchild);
}

void postOrder(Node* root) {            //后缀表达式
    if (root == NULL) return;
    postOrder(root->lchild);
    postOrder(root->rchild);
    printf("%c ", root->data);
}

void inOrder(Node* root, int layer) {    //中缀表达式
    if (root == NULL) return;
    if (root->lchild == NULL && root->rchild == NULL) {
        //叶结点是操作数，直接输出，不加括号
        printf("%c", root->data);
    } else {
        //非叶节点是操作符，需加括号（第0层根节点除外）
        if (layer > 0) printf("(");
        inOrder(root->lchild, layer + 1);
        printf("%c", root->data);
        inOrder(root->rchild, layer + 1);
        if (layer > 0) printf(")");
    }
}

double calc(double a, double b, char op) {
    switch (op) {
    case '+': return a + b;
    case '-': return a - b;
    case '*': return a * b;
    case '/': return a / b;
    }
}

double calculateExprTree(Node* root) {
    if (root == NULL) return 0;
    if (root->lchild == NULL && root->rchild == NULL) {
        //叶节点，节点存放的是 操作数
        return root->data - '0';
    }
    //非叶结点，节点存放的是 操作符
    double a = calculateExprTree(root->lchild);
    double b = calculateExprTree(root->rchild);
    return calc(a, b, root->data);
}

int main() {
    int N;
    scanf("%d\n", &N);
    Node* nodes = new Node[N];
    for (int i = 0; i < N; i++) {
        int index;
        char data;
        int l, r;
        scanf("%d %c %d %d\n", &index, &data, &l, &r);
        nodes[index].data = data;
        nodes[index].lchild = (l != -1 ? &nodes[l] : NULL);
        nodes[index].rchild = (r != -1 ? &nodes[r] : NULL);
    }
    Node* root = &nodes[0];

    inOrder(root, 0);
    printf("\n");

    preOrder(root);
    printf("\n");

    postOrder(root);
    printf("\n");

    double ans = calculateExprTree(root);
    printf("%.2f\n", ans);

    return 0;
}

enum Operator { Add, Subtract, Multiply, Divide };

struct Node {
    double num;
    Operator op;
    int type;    //0-运算数，1-二元运算符
    Node *lchild, *rchild;
};

求某节点到根节点的路径

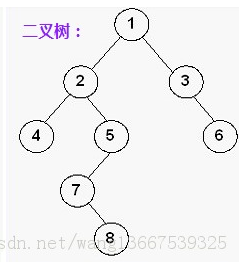
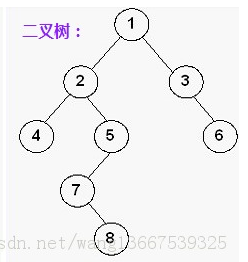
对于如下二叉树，节点7位于第4层，其到跟节点的路径为1 2 5 7

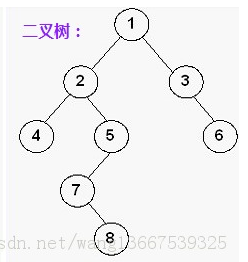
求某节点所在层数

先把问题简化一下，求二叉树指定节点所在层数（假设根节点的层数为1）

为了记录当前访问节点的层号，对于层号，可以采用以下两种方式：

1. 使用全局变量

int layer = 0;
bool flag1 = false;    //flag标记可用于提前快速结束递归的执行
void getNodeLayer(Node* root, int x) {
    if (root == NULL) return;
    if (flag1) return;
    layer++;
    if (root->data == x) {
        printf("%d\n", layer);
        flag1 = true;
        return;
    }
    getNodeLayer(root->lchild, x);
    getNodeLayer(root->rchild, x);
    layer--;
}

int main(){
    //......
    getNodeLayer(root, 7);
}

1. 使用函数传参（值传递）

bool flag1 = false;    //flag标记可用于提前快速结束递归的执行
void getNodeLayer(Node* root, int x, int layer) {
    if (root == NULL) return;
    if (flag1) return;
    if (root->data == x) {
        printf("%d\n", layer);
        flag1 = true;
        return;
    }
    getNodeLayer(root->lchild, x, layer + 1);
    getNodeLayer(root->rchild, x, layer + 1);
}

int main(){
    //......
    getNodeLayer(root, 7, 1);
}

1. 使用函数传参（传指针/引用）

bool flag1 = false;    //flag标记可用于提前快速结束递归的执行
void getNodeLayer(Node* root, int x, int &layer) {
    if (root == NULL) return;
    if (flag1) return;
    layer++;
    if (root->data == x) {
        printf("%d\n", layer);
        flag1 = true;
        return;
    }
    getNodeLayer(root->lchild, x, layer);
    getNodeLayer(root->rchild, x, layer);
    layer--;
}

int main() {
    //.......
    int layer = 0;
    getNodeLayer(root, 7, layer);
}

1. 将递归函数封装

void getNodeLayer(Node* root, int x, int &layer, int &ans, bool &flag) {
    if (root == NULL) return;
    if (flag) return;
    layer++;
    if (root->data == x) {
        ans = layer;
        flag = true;
        return;
    }
    getNodeLayer(root->lchild, x, layer, ans, flag);
    getNodeLayer(root->rchild, x, layer, ans, flag);
    layer--;
}

int getNodeLayer(Node* root, int x) {
    int ans;
    int layer = 0;
    bool flag = false;
    getNodeLayer(root, x, layer, ans, flag);
    return ans;
}

求节点路径

1. 使用全局数组

vector<int> path;
bool flag2 = false;
void getNodePath(Node* root, int x) {
    if (root == NULL) return;
    if (flag2) return;
    path.push_back(root->data);
    if (root->data == x) {
        for (int x : path) {    //输出栈的内容
            printf("%d ", x);
        }
        flag2 = true;
        return;
    }
    getNodePath(root->lchild, x);
    getNodePath(root->rchild, x);
    path.pop_back();
}

vector<int> vec {1,2,3,4,5,6,7,8,9,10};
for (int i = 0; i < vec.size(); i++）{
    printf("%d ", vec[i]);
}
//C++11特性：范围的For循环（range-based-for）
for (int x : vec) {    //这样写对于容器内的每个元素是只读的
    printf("%d ", x);
}

1. 使用函数传参（传指针/引用）

bool flag = false;
void getNodePath(Node* root, int x, vector<int> &path) {
    if (root == NULL) return;
    if (flag) return;
    path.push_back(root->data);
    if (root->data == x) {
        for (int x : path) {    //输出栈path的内容
            printf("%d ", x);
        }
        flag = true;
        return;
    }
    getNodePath(root->lchild, x, path);
    getNodePath(root->rchild, x, path);
    path.pop_back();
}

int main() {
    //......
    int x = 7;
    vector<int> path;
    getNodePath(root, x, path);
}

1. 使用函数传参（值传递）

不推荐，每次递归调用时，都会对path数组进行复制，时间和空间效率都很低

bool flag = false;
void getNodePath(Node* root, int x, vector<int> path) {
    if (root == NULL) return;
    if (flag) return;
    path.push_back(root->data);
    if (root->data == x) {
        for (int x : path) {    //输出栈path的内容
            printf("%d ", x);
        }
        flag = true;
        return;
    }
    getNodePath(root->lchild, x, path);
    getNodePath(root->rchild, x, path);
    //注意这里没有path.pop_back()
}

int main() {
    //......
    int x = 7;
    vector<int> path;
    getNodePath(root, x, path);
}

完整代码

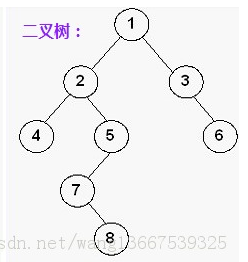
对于如下二叉树，节点7位于第4层，其到跟节点的路径为1 2 5 7

#include <iostream>
#include <vector>
using namespace std;

struct Node {
    int data;
    Node *lchild, *rchild;

    Node(int x = 0) { data = x; lchild = rchild = NULL; }

    void setChildNode(Node* l, Node* r) {
        lchild = l;
        rchild = r;
    }
};

int layer = 0;
bool flag1 = false;    //flag标记可用于提前快速结束递归的执行
void getNodeLayer(Node* root, int x) {
    if (root == NULL) return;
    if (flag1) return;
    layer++;
    if (root->data == x) {
        printf("%d\n", layer);
        flag1 = true;
        return;
    }
    getNodeLayer(root->lchild, x);
    getNodeLayer(root->rchild, x);
    layer--;
}

vector<int> path;
bool flag2 = false;
void getNodePath(Node* root, int x) {
    if (root == NULL) return;
    if (flag2) return;
    path.push_back(root->data);
    if (root->data == x) {
        for (int x : path) {    //输出栈path的内容
            printf("%d ", x);
        }
        flag2 = true;
        return;
    }
    getNodePath(root->lchild, x);
    getNodePath(root->rchild, x);
    path.pop_back();
}

int main() {
    Node* root = new Node(1);
    Node* node_2 = new Node(2);
    Node* node_3 = new Node(3);
    Node* node_4 = new Node(4);
    Node* node_5 = new Node(5);
    Node* node_6 = new Node(6);
    Node* node_7 = new Node(7);
    Node* node_8 = new Node(8);

    root->setChildNode(node_2, node_3);
    node_2->setChildNode(node_4, node_5);
    node_3->setChildNode(NULL, node_6);
    node_5->setChildNode(node_7, NULL);
    node_7->setChildNode(NULL, node_8);

    int x = 7;
    getNodeLayer(root, x);
    getNodePath(root, x);
    printf("\n");

    return 0;
}

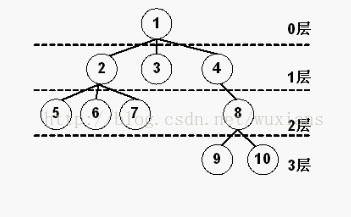
普通树的遍历

#include <iostream>
#include <vector>
#include <queue>
#include <initializer_list>
using namespace std;

struct Node {
    int data;
    vector<Node*> child;

    Node(int x = 0) { data = x; }

    void setChildNode(initializer_list<Node*> il) {
        //C++11特性：initializer_list
        for (Node* x : il) {
            child.push_back(x);
        }
    }
};

void preOrder(Node* root) {
    if (root == NULL) return;
    printf("%d ", root->data);
    for (Node* x : root->child) {
        preOrder(x);
    }
}

void postOrder(Node* root) {
    if (root == NULL) return;
    for (Node* x : root->child) {
        postOrder(x);
    }
    printf("%d ", root->data);
}

void levelOrder(Node* root) {
    if (root == NULL) return;
    queue<Node*> Q;
    Q.push(root);
    while (Q.empty() == false) {
        Node* t = Q.front(); Q.pop();
        printf("%d ", t->data);
        for (Node* x : t->child) {
            Q.push(x);
        }
    }
    printf("\n");
}

int main() {
    Node* root = new Node(1);
    Node* node_2 = new Node(2);
    Node* node_3 = new Node(3);
    Node* node_4 = new Node(4);
    Node* node_5 = new Node(5);
    Node* node_6 = new Node(6);
    Node* node_7 = new Node(7);
    Node* node_8 = new Node(8);
    Node* node_9 = new Node(9);
    Node* node_10 = new Node(10);

    root->setChildNode({ node_2,node_3,node_4 });
    node_2->setChildNode({ node_5,node_6,node_7 });
    node_4->setChildNode({ node_8 });
    node_8->setChildNode({ node_9,node_10 });

    preOrder(root);
    printf("\n");

    postOrder(root);
    printf("\n");

    levelOrder(root);

    return 0;
}

递归调用原理

函数调用栈实例：主函数main()调用funcA()，funcA()调用funcB()，funcB()再自我调用（递归）

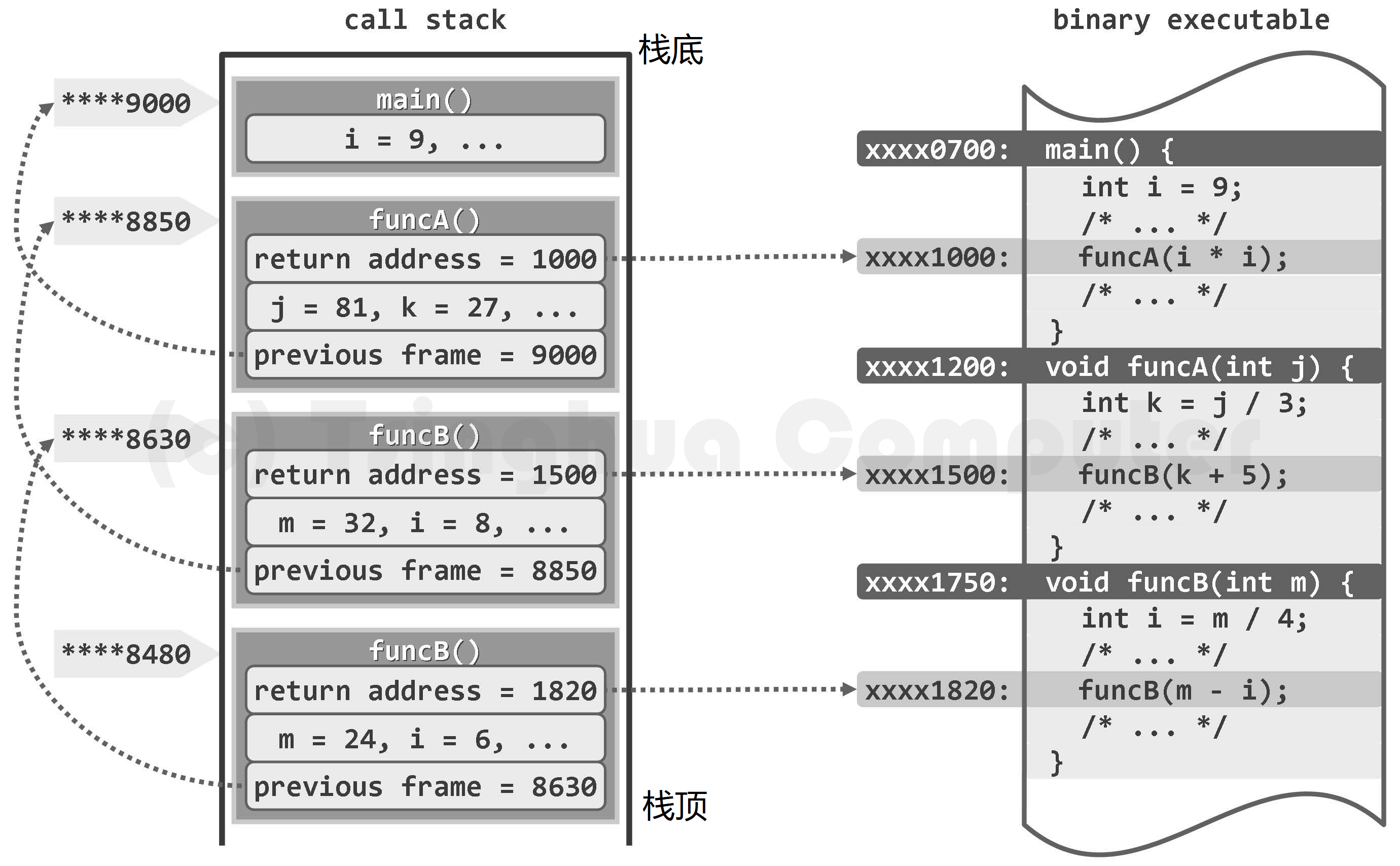
函数调用栈的基本单位是帧（frame）。每次函数调用时，都会相应地创建一帧， 记录该函数实例在二进制程序中的返回地址（return address），以及局部变量、传入参数等， 并将该帧压入调用栈。若在该函数返回之前又发生新的调用，则同样地要将与新函数对应的一帧压入栈中，成为新的栈顶。函数一旦运行完毕，对应的帧随即弹出，运行控制权将被交还给该函 数的上层调用函数，并按照该帧中记录的返回地址确定在二进制程序中继续执行的位置。

在任一时刻，调用栈中的各帧，依次对应于那些尚未返回的调用实例，亦即当时的活跃函数实例（active function instance）。特别地，位于栈底的那帧必然对应于入口主函数main()， 若它从调用栈中弹出，则意味着整个程序的运行结束，此后控制权将交还给操作系统。

此外，调用栈中各帧还需存放其它内容。比如，因各帧规模不一，它们还需记录前一帧的起始地址，以保证其出栈之后前一帧能正确地恢复。

作为函数调用的特殊形式，递归也可借助上述调用栈得以实现。比如在上图中，对应于 funcB()的自我调用，也会新压入一帧。可见，同一函数可能同时拥有多个实例，并在调用栈中 各自占有一帧。这些帧的结构完全相同，但其中同名的参数或变量，都是独立的副本。比如在 funcB()的两个实例中，入口参数m和内部变量i各有一个副本。

DFS/回溯算法

如果某问题的解可以由多个步骤得到，而每个步骤都有若干种选择（这些候选方案集可能会依赖之前做出的选择），且可以用递归枚举法实现，则它的工作方式可以用解答树来描述。

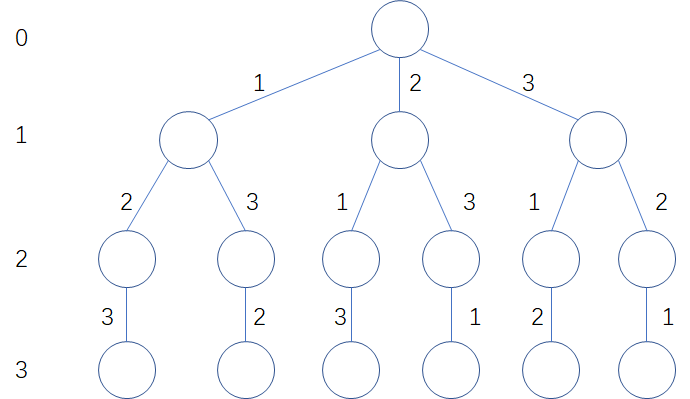
全排列问题

输出数字1~N所能组成的所有全排列

#include <iostream>
#include <vector>
using namespace std;
const int MAXN = 10;

bool isUsed[MAXN];
vector<int> num;
int N;

void DFS(int index) {
    if (index >= N) {
        for (int x : num) {
            printf("%d ", x);
        }
        printf("\n");
        return;
    }
    for (int i = 1; i <= N; i++) {
        if (isUsed[i]) continue;
        num.push_back(i);
        isUsed[i] = true;
        DFS(index + 1);
        num.pop_back();
        isUsed[i] = false;
    }
}

int main() {
    N = 3;
    DFS(0);        //从第0层开始搜索
    return 0;
}

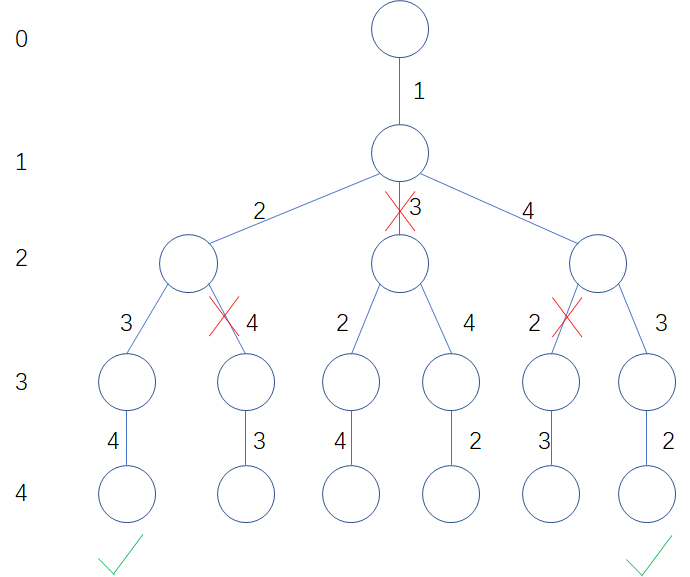
素数环问题

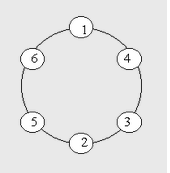
将1到n这n个整数围成一个圆环，若其中任意2个相邻的数字相加，结果均为素数，那么这个环就成为素数环。

例如数字1-6所组成的一个素数环，用数组表示是[1, 4, 3, 2, 5, 6]（第一位固定为1）

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int MAXN = 100;

bool isPrimeNum[MAXN];
vector<int> ans;
bool isUsed[MAXN];
int N;

void getPrimeTable() {    //筛选法求质数
    fill(isPrimeNum, isPrimeNum + MAXN, true);    //先假设都是素数
    isPrimeNum[0] = isPrimeNum[1] = false;
    for (int i = 2; i < MAXN; i++) {    //从2开始，因为2是最小的质素
        if (isPrimeNum[i]) {
            //把i的倍数全部设置成非质数
            //比如i=2，则把4、6、9...设置成非质数
            //若i=3，则把6、9、12、15...设置成非质数
            for (int j = 2 * i; j < MAXN; j += i) {    //注意该for循环的写法，容易出错
                isPrimeNum[j] = false;
            }
        }
    }
}

void DFS(int index) {
    if (index >= N) {
        int temp = ans[0] + ans[index - 1];    //判断第一个数和最后一个数相加后是否是质数
        if (isPrimeNum[temp] == false) return;
        for (int x : ans) {
            printf("%d ", x);
        }
        printf("\n");
        return;
    }
    for (int i = 2; i <= N; i++) {
        if (isUsed[i]) continue;
        int temp = ans[index - 1] + i;
        if (isPrimeNum[temp] == false) {
            continue;    //剪枝
        }
        ans.push_back(i);
        isUsed[i] = true;
        DFS(index + 1);
        ans.pop_back();
        isUsed[i] = false;
    }
}

int main() {
    getPrimeTable();

    N = 4;
    ans.push_back(1);    //素数环第一个数固定是1
    DFS(1);    //从第二个数开始搜索

    return 0;
}

八皇后问题

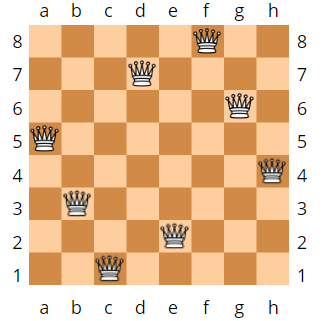
八皇后问题是一个以国际象棋为背景的问题：如何能够在8×8的国际象棋棋盘上放置八个皇后，使得任何一个皇后都无法直接吃掉其他的皇后？为了达到此目的，任两个皇后都不能处于同一条横行、纵行或斜线上。八皇后问题可以推广为更一般的n皇后摆放问题：这时棋盘的大小变为n×n，而皇后个数也变成n。当且仅当n = 1或n ≥ 4时问题有解。

#include <cstdio>
#include <algorithm>
using namespace std;

const int MAXN = 100;
int solution[MAXN];    //solution[i]=j 表示棋盘的第i行第j列放有皇后
int cnt;
int N;

char chessboard[MAXN][MAXN];
void printSolution() {
    fill(chessboard[0], chessboard[0] + MAXN * MAXN, '*');
    for (int i = 0; i < N; i++) {
        int j = solution[i];
        chessboard[i][j] = '#';
        chessboard[i][N] = '\0';
    }
    printf("solution #%d\n", cnt);
    for (int i = 0; i < N; i++) {
        printf("%s\n", chessboard[i]);
    }
    printf("\n");
}

bool judge(int row, int col) {
    for (int i = 0; i < row; i++) {
        int j = solution[i];
        if (j == col || row + col == i + j || row - col == i - j)
            return false;
    }
    return true;
}

void DFS(int row) {
    if (row >= N) {
        cnt++;
        printSolution();
        return;
    }
    for (int col = 0; col < N; col++) {
        if (judge(row, col) == false) continue;
        solution[row] = col;
        DFS(row + 1);
    }
}

int main() {
    N = 8;
    DFS(0);
    printf("N = %d, total solutions: %d\n", N, cnt);
    return 0;
}