title: 剑指offer算法题
date: 2019-03-12 09:39:48
categories: 代码
tags: 算法学习

剑指offer算法题

数据结构

二维数组中的查找

题目描述

给定一个二维数组，其每一行从左到右递增排序，从上到下也是递增排序。给定一个数，判断这个数是否在该二维数组中。

  1. Consider the following matrix:
  2. [
  3.   [1,   4,  7, 11, 15],
  4.   [2,   5,  8, 12, 19],
  5.   [3,   6,  9, 16, 22],
  6.   [10, 13, 14, 17, 24],
  7.   [18, 21, 23, 26, 30]
  8. ]
  9. Given target = 5, return true.
  10. Given target = 20, return false.

解题思路

要求时间复杂度 O(M + N)，空间复杂度 O(1)。

该二维数组中的一个数，它左边的数都比它小，下边的数都比它大。因此，从右上角开始查找，就可以根据 target 和当前元素的大小关系来缩小查找区间，当前元素的查找区间为左下角的所有元素。

{% asset_img 二维数组.gif 二维数组 %}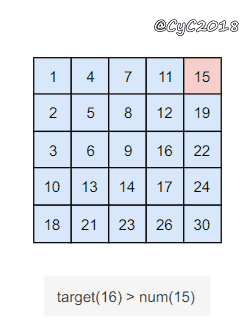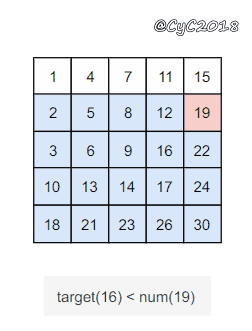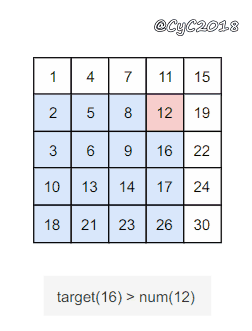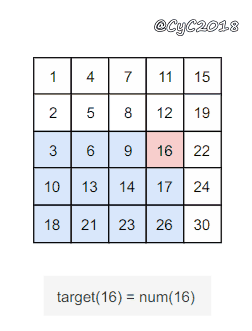
二维数组.gif

  1. public class Test03 {
  3.     /**
  4.      * 在一个二维数组中，每一行从左到右递增，每一列从上到下递增。
  5.      * 完成一个函数，输入一个这样的二维数组和一个整数，判断数组中是否含有该整数
  6.      *
  7.      * 解题思路： 首先选取右上角的数字，如果右上角的数字等于要查找的数字，结束。
  8.      * 如果该数字大于要查找的数字，剔除该数字所在列，如果该数字小于要查找的数字，剔除该数字所在行
  9.      * 该方法每一次都剔除一行或一列。进一步缩小范围
  10.      *
  11.      * @param matrix 二维数组
  12.      * @param number 要查找的
  13.      * @return 查找结果 true找到，false没有找到
  14.      */
  15.     public static boolean find(int[][] matrix, int number) {
  16.         if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
  17.             return false;
  18.         }
  20.         int rows = matrix.length; //数组行数
  21.         int cols = matrix[0].length; //数组行的列数
  23.         //确保从右上角开始
  24.         int r=0;
  25.         int c =cols-1;
  27.         //要查找的位置确保在数组内
  28.         while (r <= rows - 1 && c >= 0) {
  29.             if (number == matrix[r][c]) {
  30.                 return true;
  31.             } else if (number > matrix[r][c]) {
  32.                 r++; //行数加一表示向下移动
  33.             } else {
  34.                 c--; //列数减一表示向左移动
  35.             }
  36.         }
  37.         return false;
  38.     }
  41.     /**
  42.      * 测试数据
  43.      * @param args
  44.      */
  45.     public static void main(String[] args){
  47.         int[][] matrix = {
  48.                 {1, 2, 8, 9},
  49.                 {2, 4, 9, 12},
  50.                 {4, 7, 10, 13},
  51.                 {6, 8, 11, 15}
  52.         };
  54.         System.out.println(find(matrix, 7));    // 要查找的数在数组中
  55.         System.out.println(find(matrix, 5));    // 要查找的数不在数组中
  56.         System.out.println(find(matrix, 1));    // 要查找的数是数组中最小的数字
  57.         System.out.println(find(matrix, 15));   // 要查找的数是数组中最大的数字
  58.         System.out.println(find(matrix, 0));    // 要查找的数比数组中最小的数字还小
  59.         System.out.println(find(matrix, 16));   // 要查找的数比数组中最大的数字还大
  60.         System.out.println(find(null, 16));     // 健壮性测试，输入空指针
  61.     }
  62. }

替换空格

题目描述

将一个字符串中的空格替换成 “%20”。

  1. Input:
  2. "A B"
  4. Output:
  5. "A%20B"

解题思路

{% asset_img 替换过程.png 替换过程 %}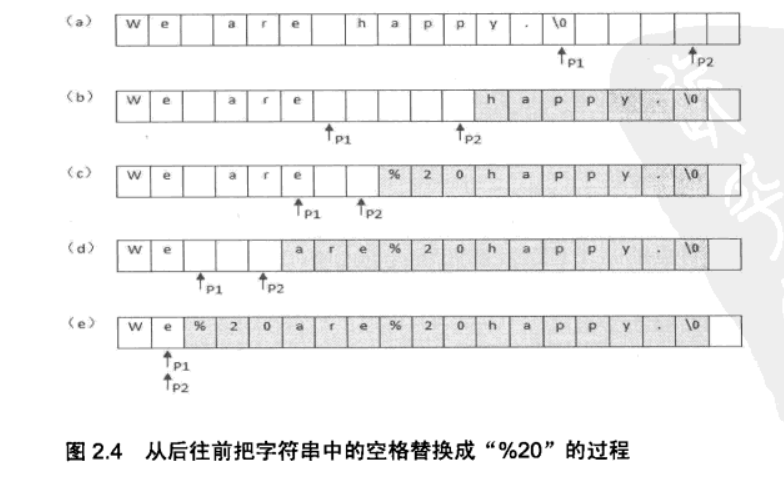
替换过程.png

在字符串尾部填充任意字符，使得字符串的长度等于替换之后的长度。因为一个空格要替换成三个字符，因此当遍历到一个空格时，需要在尾部填充两个任意字符。

令 P1 指向字符串原来的末尾位置，P2 指向字符串现在的末尾位置。P1 和 P2 从后向前遍历，当 P1 遍历到一个空格时，就需要令 P2 指向的位置依次填充 02%（注意是逆序的），否则就填充上 P1 指向字符的值。

从后向前遍是为了在改变 P2 所指向的内容时，不会影响到 P1 遍历原来字符串的内容。
{% asset_img 替换空格.gif 替换空格 %}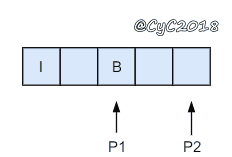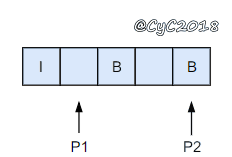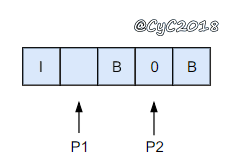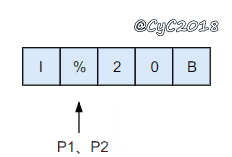
替换空格.gif

  1. public String replaceSpace(StringBuffer str) {
  3.         int p1 = str.length() - 1;//最后一位
  6.         //统计字符数组中的空白字符数
  7.         for (int i = 0; i < p1; i++) {
  8.             if (str.charAt(i) == ' ') {
  9.                 str.append(" ");//生成新的长度的字符串
  10.             }
  11.         }
  13.         //最后一位
  14.         int p2 = str.length()-1;
  17.         //p1与p2重合时循环结束
  18.         while (p1 >= 0 && p2 > p1) {
  20.             char c = str.charAt(p1--);
  21.             if (c == ' ') {
  22.                 str.setCharAt(p2--, '0');
  23.                 str.setCharAt(p2--, '2');
  24.                 str.setCharAt(p2--, '%');
  25.             } else {
  26.                 //如果c不等于空格，则将c向后移动到p2的位置
  27.                 str.setCharAt(p2--, c);
  28.             }
  29.         }
  30.         return str.toString();
  31.     }

从尾到头打印链表

问题描述

从尾到头反过来打印链表的值

{% asset_img 倒序打印链表.gif 倒序打印链表 %}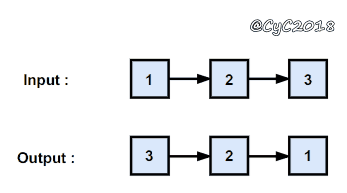
倒序打印链表.gif

解题思路

{% asset_img 使用递归.gif 使用递归 %}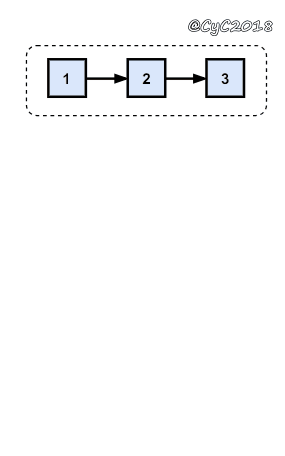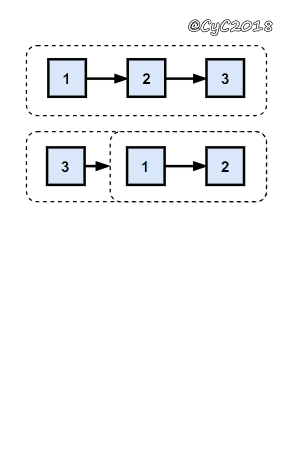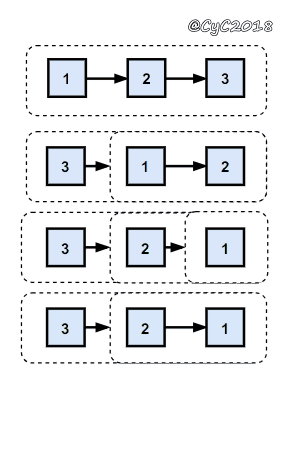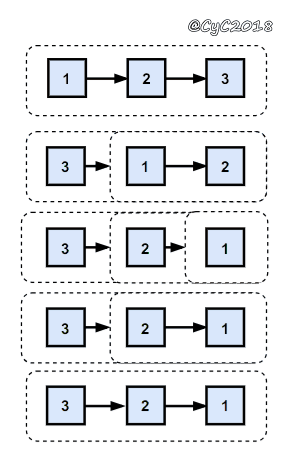
使用递归.gif

使用递归
  1. public class ListNode {
  2.     int val;
  3.     ListNode next = null;
  5.     ListNode(int val) {
  6.         this.val = val;
  7.     }
  8. }
  10. public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
  11.     ArrayList<Integer> ret = new ArrayList<>();
  12.     if (listNode != null) {
  13.         ret.addAll(printListFromTailToHead(listNode.next));
  14.         ret.add(listNode.val);
  15.     }
  16.     return ret;
  17. }

使用头插法

利用链表头插法为逆序的特点。

头结点和第一个节点的区别：

  1. 头结点是在头插法中使用的一个额外节点，这个节点不存储值；
  2. 第一个节点就是链表的第一个真正存储值的节点。

{% asset_img 头插法.gif 头插法 %}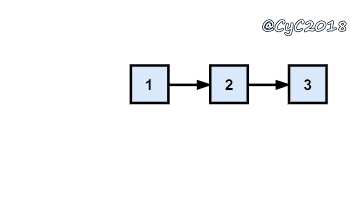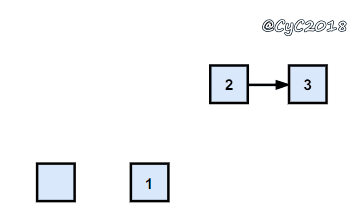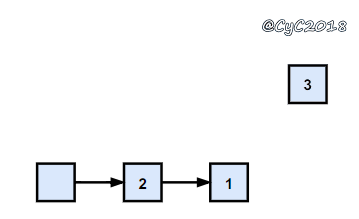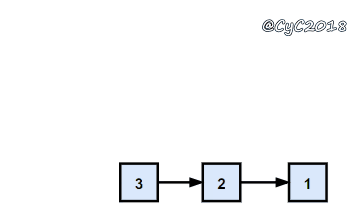
头插法.gif

  1. public class ListNode {
  2.     int val;
  3.     ListNode next = null;
  5.     ListNode(int val) {
  6.         this.val = val;
  7.     }
  8. }
  10. public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
  11.     // 头插法构建逆序链表
  12.     ListNode head = new ListNode(-1);//建立新的头结点
  13.     while (listNode != null) { //链表不空
  14.         ListNode memo = listNode.next; //链表的下一个节点
  15.         listNode.next = head.next;
  16.         head.next = listNode;
  17.         listNode = memo;
  18.     }
  19.     // 构建 ArrayList
  20.     ArrayList<Integer> ret = new ArrayList<>();
  21.     head = head.next;
  22.     while (head != null) {
  23.         ret.add(head.val);
  24.         head = head.next;
  25.     }
  26.     return ret;
  27. }

使用栈

{% asset_img 使用栈.gif 栈 %}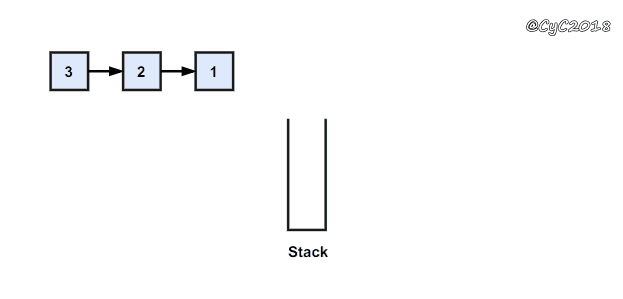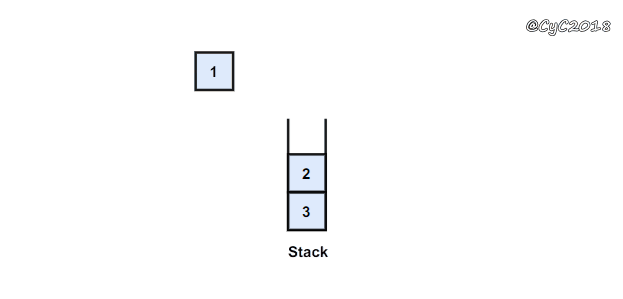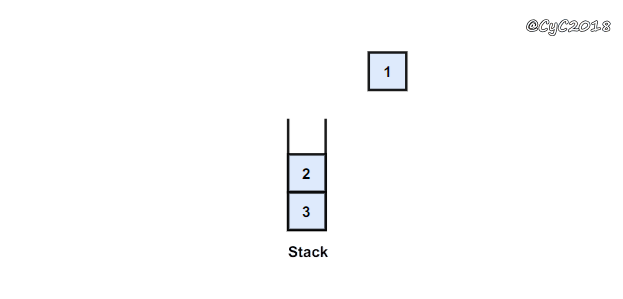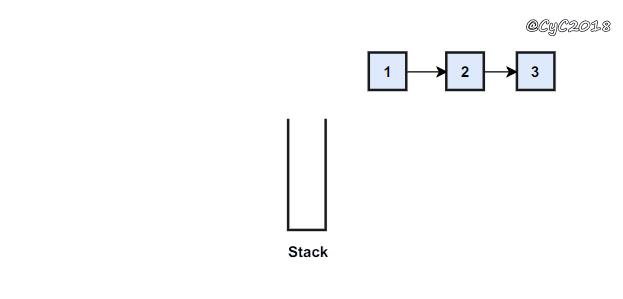
使用栈.gif

  2. public class ListNode {
  3.     int val;
  4.     ListNode next = null;
  6.     ListNode(int val) {
  7.         this.val = val;
  8.     }
  9. }
  11. public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
  12.     Stack<Integer> stack = new Stack<>();
  13.     while (listNode != null) {
  14.         stack.add(listNode.val);
  15.         listNode = listNode.next;
  16.     }
  17.     ArrayList<Integer> ret = new ArrayList<>();
  18.     while (!stack.isEmpty())
  19.         ret.add(stack.pop());
  20.     return ret;
  21. }

重建二叉树

题目描述

根据二叉树的前序遍历和中序遍历的结果，重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

  1. preorder = [3,9,20,15,7]
  2. inorder =  [9,3,15,20,7]

{% asset_img 重建二叉树.gif 重建二叉树 %}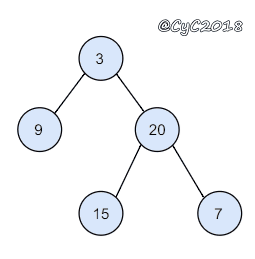
重建二叉树.gif

解题思路

前序遍历的第一个值为根节点的值，使用这个值将中序遍历结果分成两部分，左部分为树的左子树中序遍历结果，右部分为树的右子树中序遍历的结果。

{% asset_img 二叉树.gif 二叉树 %}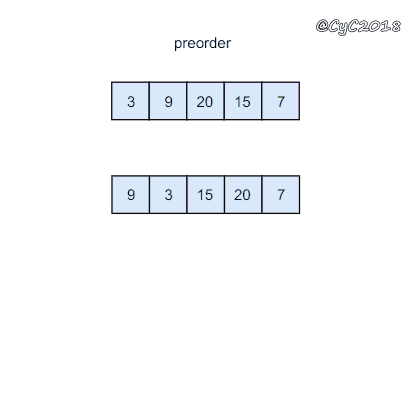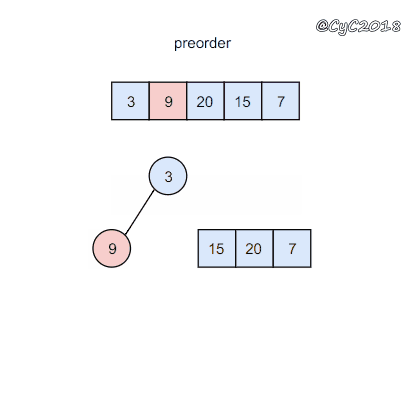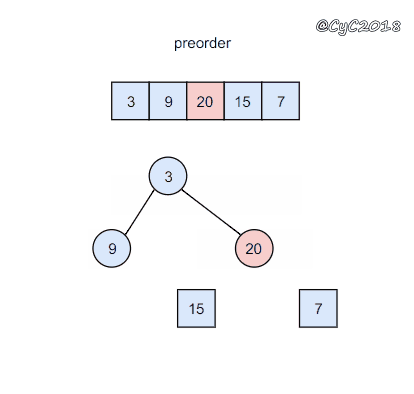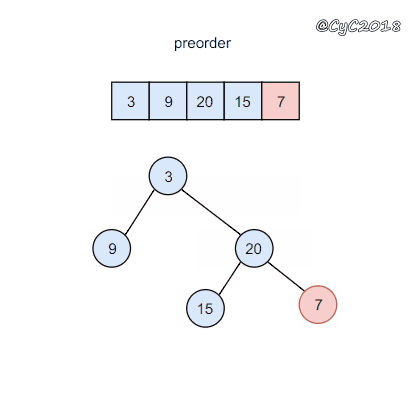
二叉树.gif

方法1：

  1. /**
  2.  * Definition for binary tree
  3.  * public class TreeNode {
  4.  *     int val;
  5.  *     TreeNode left;
  6.  *     TreeNode right;
  7.  *     TreeNode(int x) { val = x; }
  8.  * }
  9.  */
  11. public class CB1{
  12.     /**
  13.      * 重建二叉树
  14.      * 
  15.      * @param pre 先序序列
  16.      * @param in  中序序列
  17.      * @return 二叉树根结点
  18.      */
  19.     public TreeNode reConstructBinaryTree(int[] pre, int[] in) {
  20.         if (pre == null || in == null || pre.length != in.length) {
  21.             return null;
  22.         }
  23.         int n = pre.length;
  24.         return constructBinaryTree(pre, 0, n - 1, in, 0, n - 1);
  25.     }
  27.     private TreeNode constructBinaryTree(int[] pre, int startPre, int endPre, int[] in, int startIn, int endIn) {
  28.         TreeNode node = new TreeNode(pre[startPre]);
  29.         if (startPre == endPre) {
  30.             if (startIn == endIn) {
  31.                 return node;
  32.             }
  33.             throw new IllegalArgumentException("Invalid input!");
  34.         }
  36.         int inOrder = startIn;
  37.         while (in[inOrder] != pre[startPre]) {
  38.             ++inOrder;
  39.             if (inOrder > endIn) {
  40.                 new IllegalArgumentException("Invalid input!");
  41.             }
  42.         }
  43.         int len = inOrder - startIn;
  44.         if (len > 0) {
  45.             // 递归构建左子树
  46.             node.left = constructBinaryTree(pre, startPre + 1, startPre + len, in, startIn, inOrder - 1);
  47.         }
  49.         if (inOrder < endIn) {
  50.             // 递归构建右子树
  51.             node.right = constructBinaryTree(pre, startPre + len + 1, endPre, in, inOrder + 1, endIn);
  52.         }
  53.         return node;
  55.     }
  56. }

用两个栈实现队列

问题描述

题目： 用两个栈实现一个队列。请实现它的两个函数，appendTail和deleteHead，分别完成在队列尾部和插入节点和在队列头部删除节点的功能。
即实现push和pop操作。

解题思路

stack1 栈用来处理入栈（push）操作，stack2 栈用来处理出栈（pop）操作。一个元素进入 stack1 栈之后，出栈的顺序被反转。当元素要出栈时，需要先进入 stack2 栈，此时元素出栈顺序再一次被反转，因此出栈顺序就和最开始入栈顺序是相同的，先进入的元素先退出，这就是队列的顺序。

{% asset_img 队列.gif %}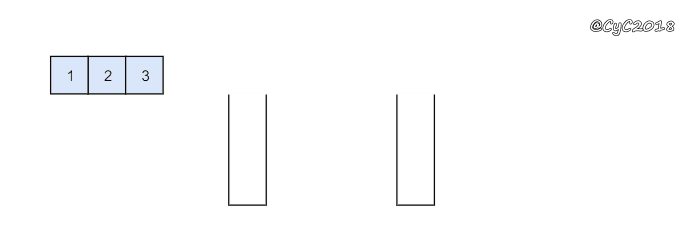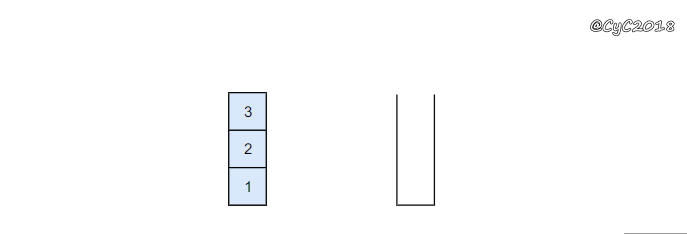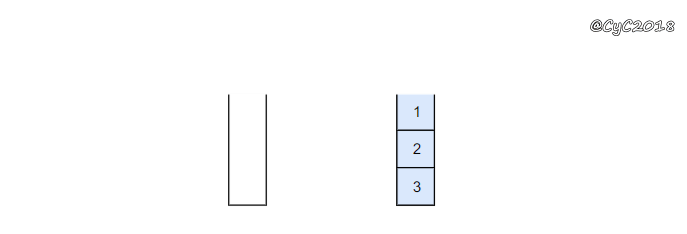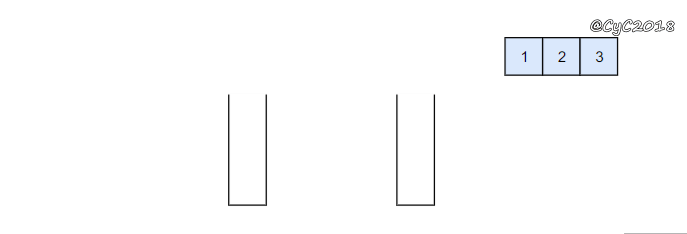
队列.gif
{% asset_img 实现队列.png %}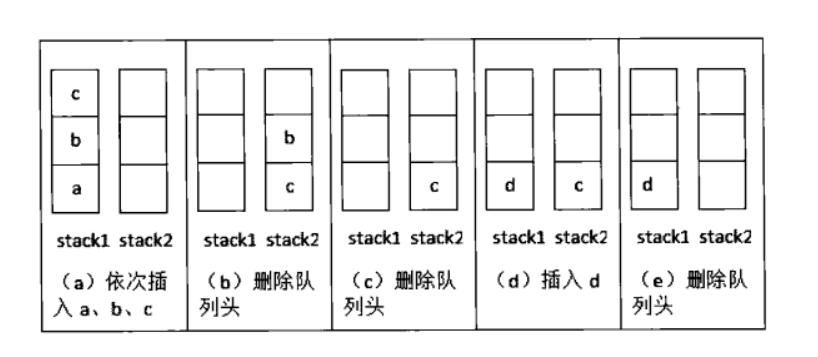
实现队列.png

  1. Stack<Integer> in = new Stack<Integer>();
  2. Stack<Integer> out = new Stack<Integer>();
  4. public void push(int node) {
  5.     in.push(node);
  6. }
  8. public int pop() throws Exception {
  9.     if (out.isEmpty())
  10.         while (!in.isEmpty())
  11.             out.push(in.pop());
  13.     if (out.isEmpty())
  14.         throw new Exception("queue is empty");
  16.     return out.pop();
  17. }

排序和查找

旋转数组的最小数字

问题描述

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个非递减排序的数组的一个旋转，输出旋转数组的最小元素。

例如数组 {3, 4, 5, 1, 2} 为 {1, 2, 3, 4, 5} 的一个旋转，该数组的最小值为 1。

解题思路

在一个有序数组中查找一个元素可以用二分查找，二分查找也称为折半查找，每次将查找区间减半，这种这般特性的算法复杂度都为O(logN)。

本题可以修改二分查找算法进行求解：

  • 当 nums[m] <= nums[h] 的情况下，说明解在 [l, m] 之间，此时令 h = m；
  • 否则解在 [m + 1, h] 之间，令 l = m + 1。

{% asset_img 二分.png %}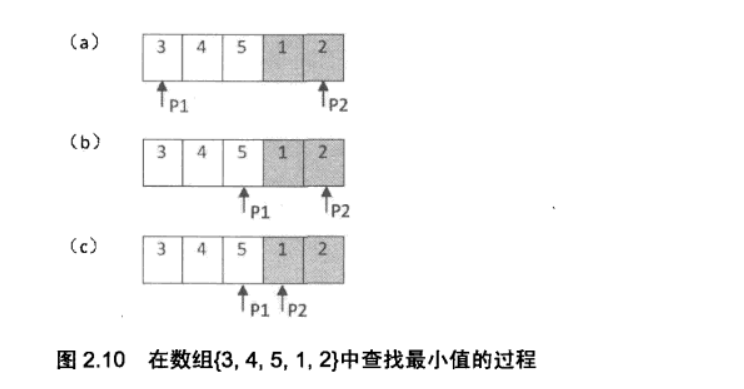
二分.png

  1. public int min(int[] nums){
  2.         if (nums.length == 0){
  3.             return 0;
  4.         }
  6.         int l = 0, h = nums.length - 1;
  7.         while (l < h) {
  8.             int m = 1 + (h - 1) / 2;
  9.             if (nums[m] <= nums[h]) {
  10.                 h = m;
  11.             } else {
  12.                 l = m+1;
  13.             }
  14.         }
  15.         return nums[l];
  16.     }

如果允许数组元素重复的话，那么会出现特殊的情况：nums[l] == nums[m] == nums[h],那么此时无法确定解在哪个区间，需要切换到顺序查找。例如对于数组 {1,1,1,0,1}，l、m 和 h 指向的数都为 1，此时无法知道最小数字 0 在哪个区间。

斐波那契数列

题目描述

求斐波那契数列的第 n 项，n <= 39。
{% asset_img fib.jpg %}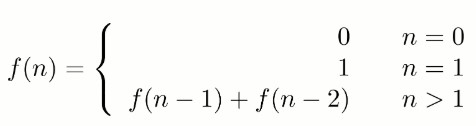
fib.jpg

解题思路

若使用递归则会重复计算一些子问题，如f(10)需要计算f(9)和f(8),计算f(9)需要计算f(8)和f(7),可以看到f(8)被重复计算。

{% asset_img fib.gif %}
fib.gif

递归是将一个问题划分为多个子问题求解，动态规划也是如此，但是动态规划会把子问题的解缓存起来，从而避免重复求解子问题。

  1. public int Fibonacci(int n){
  2.         if (n <= 1) {
  3.             return n;
  4.         }
  6.         int[] fib = new int[n + 1];
  7.         fib[1] = 1;
  9.         for (int i = 2; i<=n; i++){
  10.             fib[i] = fib[i -1] + fib[i -2];
  11.         }
  12.         return fib[n];
  13.     }

考虑到第 i 项只与第 i-1 和第 i-2 项有关，因此只需要存储前两项的值就能求解第 i 项，从而将空间复杂度由 O(N) 降低为 O(1)。

  1. public int Fibonacci2(int n){
  2.         if (n <= 1) {
  3.             return n;
  4.         }
  6.         int pre2 = 0, pre1 = 1;
  7.         int fib = 0;
  8.         for (int i =2; i<=n;i++){
  9.             fib = pre2 + pre1;
  10.             pre2 = pre1;
  11.             pre1 = fib;
  12.         }
  13.         return fib;
  14.     }

由于待求解的 n 小于 40，因此可以将前 40 项的结果先进行计算，之后就能以 O(1) 时间复杂度得到第 n 项的值了。

  1. public class Solution {
  3.     private int[] fib = new int[40];
  5.     public Solution() {
  6.         fib[1] = 1;
  7.         for (int i = 2; i < fib.length; i++)
  8.             fib[i] = fib[i - 1] + fib[i - 2];
  9.     }
  11.     public int Fibonacci(int n) {
  12.         return fib[n];
  13.     }
  14. }

矩形覆盖

题目描述

我们可以用 2 1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个 2 1的小矩形无重叠地覆盖一个2 * n的大矩形，总共有多少种方法。
{% asset_img 矩形.gif %}
矩形.gif

解题思路

  1. public int RectCover(int n){
  2.     if(n <= 2)
  3.         return n;
  4.     int pre2 = 1, pre1 = 2;
  5.     int result = 0;
  6.     for (int i = 3; i <= n; i++){
  7.         result = pre2 + pre1;
  8.         pre2 = pre1;
  9.         pre1 = result;
  10.     }
  11.     return result;
  12. }

跳台阶

题目描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级台阶总共有多少种跳法。

{% asset_img 蛙.png %}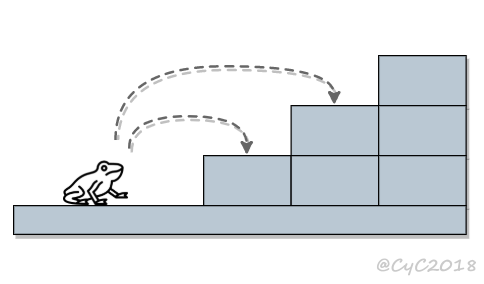
蛙.png
解题思路

  1. public int JumpFloor(int n) {
  2.     if (n <= 2)
  3.         return n;
  4.     int pre2 = 1, pre1 = 2;
  5.     int result = 1;
  6.     for (int i = 2; i < n; i++) {
  7.         result = pre2 + pre1;
  8.         pre2 = pre1;
  9.         pre1 = result;
  10.     }
  11.     return result;
  12. }

变态跳台阶

题目描述

一只青蛙一次可以跳上 1 级台阶，也可以跳上 2 级… 它也可以跳上 n 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
{% asset_img 蛙2.png %}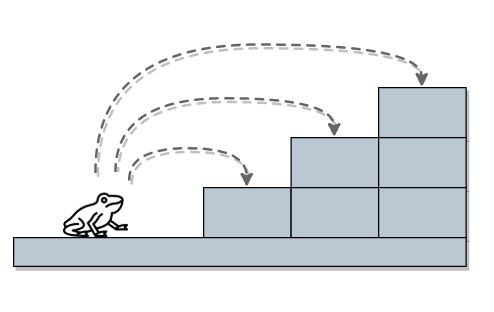
蛙2.png

解题思路

动态规划
  1. public int JumpFloorII(int target) {
  2.     int[] dp = new int[target];
  3.     Arrays.fill(dp, 1);
  4.     for (int i = 1; i < target; i++)
  5.         for (int j = 0; j < i; j++)
  6.             dp[i] += dp[j];
  7.     return dp[target - 1];
  8. }

数学推导

跳上 n-1 级台阶，可以从 n-2 级跳 1 级上去，也可以从 n-3 级跳 2 级上去…，那么

  1. f(n-1) = f(n-2) + f(n-3) + ... + f(0)

同样，跳上 n 级台阶，可以从 n-1 级跳 1 级上去，也可以从 n-2 级跳 2 级上去… ，那么

  2. f(n) = f(n-1) + f(n-2) + ... + f(0)

综上可得

  2. f(n) - f(n-1) = f(n-1)

即

  2. f(n) = 2*f(n-1)

所以 f(n) 是一个等比数列

  1. public int JumpFloorII(int target) {
  2.     return (int) Math.pow(2, target - 1);
  3. }

二进制中1的个数

题目描述

输入一个整数，输出该数二进制表示中1的个数。

n&(n-1)

该位运算除n的位级表示中最低的那一位

  1. n       : 10110100
  2. n-1     : 10110011
  3. n&(n-1) : 10110000

时间复杂度O(M),其中M表示1的个数

  1. public int NumberOf1(int n){
  2.     int cnt = 0;
  3.     while(n != 0){
  4.         cnt++;
  5.         n &= (n - 1);
  6.     }
  7.     return cnt;
  8. }

数值的整数次方

题目描述

给定一个 double 类型的浮点数 base 和 int 类型的整数 exponent，求 base 的 exponent 次方。

解题思路

下面的讨论中 x 代表 base，n 代表 exponent。
{% asset_img power.jpg %}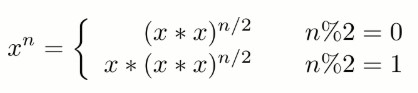
power.jpg
因为 (x*x)n/2 可以通过递归求解，并且每次递归 n 都减小一半，因此整个算法的时间复杂度为 O(logN)。

代码实现

方法1

  1. public double Power(double base, int exponent) {
  2.     if (exponent == 0)
  3.         return 1;
  4.     if (exponent == 1)
  5.         return base;
  6.     boolean isNegative = false;
  7.     if (exponent < 0) {
  8.         exponent = -exponent;
  9.         isNegative = true;
  10.     }
  11.     double pow = Power(base * base, exponent / 2);
  12.     if (exponent % 2 != 0)
  13.         pow = pow * base;
  14.     return isNegative ? 1 / pow : pow;
  15. }

方法2

  1. /**
  2.      * 实现函数double Power(double base, int exponent) 求base的exponent次方
  3.      * 不使用库函数，且不用考虑最大值问题
  4.      * @param base 指次
  5.      * @param exponent 幂
  6.      */
  7.     public static double power(double base, int exponent) {
  8.         //指数和幂不能同时为0
  9.         if (base == 0 && exponent == 0) {
  10.             throw new RuntimeException("invalid input. base and exponent both are zero");
  11.         }
  13.         if (exponent == 0) {
  14.             return 1;
  15.         }
  17.         //求指数的绝对值
  18.         long exp = exponent;
  19.         if (exponent < 0) {
  20.             exp = -exp;
  21.         }
  23.         double result = powerWithUnsignedExponent(base, exp);
  25.         //如果指数为负数，求倒数
  26.         if (exponent < 0){
  27.             result = 1 / result;
  28.         }
  29.         return result;
  30.     }
  32.     /**
  33.      * 求一个数的整数次幂，不考虑溢出
  34.      * @param base 指次
  35.      * @param exponent  幂
  36.      * @return 结果
  37.      */
  38.     public static double powerWithUnsignedExponent(double base, long exponent) {
  39.         // 如果指数为0，返回1
  40.         if (exponent == 0) {
  41.             return 1;
  42.         }
  44.         // 指数为1，返回底数
  45.         if (exponent == 1) {
  46.             return base;
  47.         }
  49.         //递归求值的一半
  50.         double result = powerWithUnsignedExponent(base, exponent >> 2);
  52.         //求最终的值,如果是基数还要乘一次底数
  53.         result *= result;
  54.         if (exponent % 2 != 0) {
  55.             result *=base;
  56.         }
  58.         return result;
  59.     }
  60.     public static void main(String[] args) {
  62.         System.out.println(0.0000000000000000000000001111 == 0);
  63.         System.out.println(0.0000000000000000000000000000 == 0);
  65.         System.out.println(power(2, -4));
  66.         System.out.println(power(2, 4));
  67.         System.out.println(power(2, 0));
  68.         System.out.println(power(0.00000000000000000000000000001, -1));
  69.         System.out.println(power(0.00000000000000000000000000001, 1));
  70.         System.out.println(power(0.00000000000000000000000000001, 0));
  71.         System.out.println(power(0.00000000000000000000000000000, 0));
  72.     }

打印从 1 到最大的 n 位数

题目描述

输入数字 n，按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3，则打印出 1、2、3 一直到最大的 3 位数即 999。

解题思路

由于 n 可能会非常大，因此不能直接用 int 表示数字，而是用 char 数组进行存储。

使用回溯法得到所有的数。

  1. public void print1ToMaxOfNDigits(int n) {
  2.         if (n <= 0) {
  3.             return;
  4.         }
  5.         char[] number = new char[n];
  6.         print1ToMaxOfNDigits(number, 0);
  7.     }
  9.     private void print1ToMaxOfNDigits(char[] number, int digit) {
  10.         if (digit == number.length) {
  11.             printNumber(number);
  12.             return;
  13.         }
  14.         for (int i = 0; i < 10; i++) {
  15.             number[digit] = (char) (1 + '0');
  16.             print1ToMaxOfNDigits(number, digit + 1);
  17.         }
  18.     }
  20.     private void printNumber(char[] number) {
  21.         int index = 0;
  22.         while (index < number.length && number[index] == '0') {
  23.             index++;
  24.         }
  25.         while (index < number.length) {
  26.             System.out.print(number[index++]);
  27.         }
  28.         System.out.println();
  29.     }

在O(1)时间内删除链表节点

解题思路

①如果该节点不是尾节点，那么可以直接将下一个节点的值赋给该节点，然后令该节点指向下下个节点，再删除下一个节点，时间复杂度为O(1)。

{% asset_img 节点.png %}
节点.png

②如果链表只有一个节点，那么直接删除节点
③否则就需要先便利列表，找到节点的前一个节点，然后让前一个节点指向null，时间复杂度为O(n).

{% asset_img 节点1.png %}
节点1.png

综上，如果进行N次操作，那么大约需要操作节点的次数为N-1+N=2N-1，其中N-1表示N-1个不是尾节点的每个节点以O(1)的时间复杂度操作节点的总次数，N表示一个尾节点以O(N)的时间复杂度操作节点的总次数，(2N-1)/N~2,因此该算法的平均时间复杂度为O(1).

  1. public class ListNode {
  2.     int val;
  3.     ListNode next = null;
  5.     ListNode(int val) {
  6.         this.val = val;
  7.     }
  8. }
  11. public ListNode deleteNode(ListNode head, ListNode toDelete) {
  12.         if (head == null || toDelete == null) {
  13.             return null;
  14.         }
  16.         if (toDelete.next != null){
  17.             //要删除的节点不是尾节点
  18.             ListNode next = toDelete.next;
  19.             toDelete.val = next.val;
  20.             toDelete.next = next.next;
  21.         }
  22.         else {
  23.             if (head == toDelete)
  24.                 //只有一个节点
  25.                 head = null;
  26.             else {
  27.                 ListNode cur = head;
  28.                 while (cur.next != toDelete)
  29.                     cur = cur.next;
  30.                 cur.next = null;
  31.             }
  32.         }
  33.         return head;
  34.     }

调整数组顺序使奇数位于偶数前面

题目描述

需要保证奇数和奇数，偶数和偶数之间的相对位置不变，这和书本不太一样。
{% asset_img 奇偶.png %}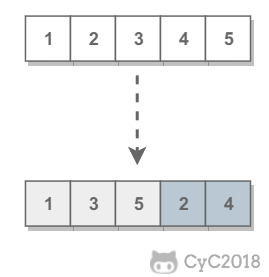
奇偶.png

解题思路

  1. public void reOrderArray(int[] nums){
  3.         int oddCnt = 0;
  4.         for (int val : nums) {
  5.             if (val % 2 ==1)
  6.                 oddCnt++;
  7.         }
  8.         int[] copy = nums.clone();
  9.         int i = 0,j = oddCnt;
  10.         for (int num: copy){
  11.             if (num % 2 == 1) {
  12.                 nums[i++] = num;
  13.             }
  14.             else {
  15.                 nums[j++] = num;
  16.             }
  17.         }
  18.     }

链表中倒数第k个节点

解题思路

设链表的长度为N,设两个指针P1和P2,先让P1移动k个节点，则还有N-K和节点可移动。此时让P1和P2同时移动，可以知道当P1移动到链表结尾时，P2移动到N-K个节点处，该位置就是倒数第K个节点。
{% asset_img 倒数K.png %}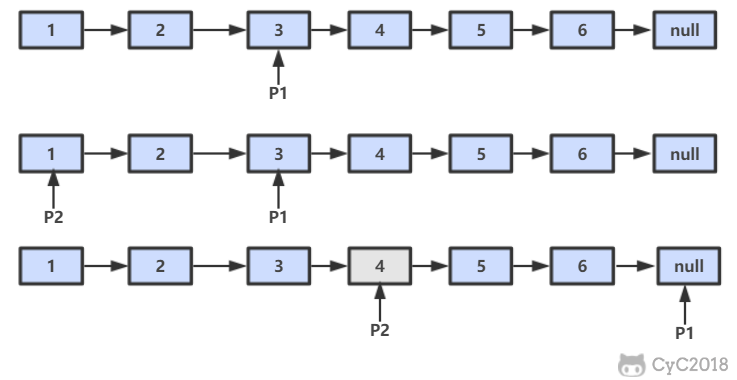
倒数K.png

  1. public ListNode FindKthToTail(ListNode head, int k){
  2.         if (head == null){
  3.             return null;
  4.         }
  5.         ListNode P1 = head;
  6.         while (P1 != null && k-->0){
  7.             P1 = P1.next;
  8.         }
  9.         if (k > 0)
  10.             return null;
  11.         ListNode P2 = head;
  12.         while (P1 != null) {
  13.             P1 = P1.next;
  14.             P2 = P2.next;
  15.         }
  16.         return P2;
  17.     }

反转链表

题目描述

{% asset_img reverse.png %}
reverse.png

解题思路

c实现
  1. 待

java实现:递归
  1. public class ListNode {
  2.     int val;
  3.     ListNode next = null;
  5.     ListNode(int val) {
  6.         this.val = val;
  7.     }
  8. }
  10. public ListNode ReverseList(ListNode head){
  11.     if(head == null || head.next == null)
  12.         return head;
  13.     ListNode next = head.next;
  14.     head.next = null;
  15.     ListNode newHead = ReverseList(next);
  16.     next.next = head;
  17.     return newHead;
  18. }

java实现：迭代
  1. public class ListNode {
  2.     int val;
  3.     ListNode next = null;
  5.     ListNode(int val) {
  6.         this.val = val;
  7.     }
  8. }
  10. public ListNode ReverseList(ListNode head){
  11.     ListNode newList = new ListNode(-1);
  12.     while (head != null){
  13.         ListNode next = head.next; //将头结点的下一个节点储存在next中
  14.         head.next = newList.next;//（头结点情况）将头结点的下一个节点储存为空值。（一般情况）实现头尾反转
  15.         newList.next = head; //存储头结点的值
  16.         head = next; //头结点向前
  17.     }
  18.     return newList.next;
  19. }