所谓归并排序就是把一个数组递归地分成两半分别排序，然后将结果归并起来。所以它的时间复杂度是O(nlogn),而因为需要辅助数组归并，空间复杂度O(n)。

1.归并操作：需要一个辅助数组来处理。

  • 归并一（自己的）： ```cpp void merge1(vector& a,int lo,int mid,int ho){//lo…mid,mid+1,…,ho vectoraux; aux.resize(ho-lo+1);
    1. int i = lo,j = mid + 1,k = 0;
    while (i <= mid && j <= jo){
    1.   if (a[i] < a[j]) aux[k++] = a[i++];
    2.   else             aux[k++] = a[j++];
    } while (i <= mid) aux[k++] = a[i++]; while (j <= ho) aux[k++] = a[j++]; a.assign(aux.begin(),aux.end());

}

  2. - 归并二：（书本上）先把所有元素都复制到aux[],再归并到a[],归并时先判断左右半边是否用完。
  3. - 归并三：（快速归并）因为a[lo,...,mid]与a[mid+1,...,ho]分别是递增有序的，把a[]中元素赋值到aux[]上时可以a[mid+1,...,ho]是逆序赋值，这样可以去掉内循环的检测半边是否已经遍历完的情况。**aux[小->大;大->小]**
  4. ```cpp
  5. void merge2(vector<int>& a,int lo,int mid,int ho){
  6.     int i = lo,j = mid+1;
  7.      vector<int>aux;
  8.     aux.resize(h0-lo+1);
  9.     for(int k = lo;k <= ho;k ++)
  10.         aux[k] = a[k];
  11.     for(int k = lo;k <= ho;k ++){
  12.         //判定是否出界
  13.         if(i > mid)               a[k] = aux[j++];//左半边已经遍历完
  14.         else if(j > ho)           a[k] = aux[i++];//右半边已经遍历完
  15.         else if(aux[j] <= aux[i]) a[k] = aux[j++];
  16.         else                      a[k] = aux[i++];
  17.     }
  18. }
  20. void merge3(vector<int>& a,int lo,int mid,int ho){
  21.     vector<int>aux;
  22.     aux.resize(h0-lo+1);
  23.     for(int k = lo;k <= mid;k ++)
  24.         aux[k] = a[k];
  25.     for(int k = mid+1;k <= ho;k ++){
  26.         aux[k] = aux[ho+mid+1-k];
  27.     //aux[小->大;大->小]
  28.     int i = lo,j = ho
  30.     for(int k = l0;k <= ho;k ++){
  31.         if(aux[i] <= aux[j]) a[k++] = aux[i++];
  32.         else                 a[k++] = aux[j++];
  33.     }
  34. }

2.自顶向下的归并排序：基于分治的思想

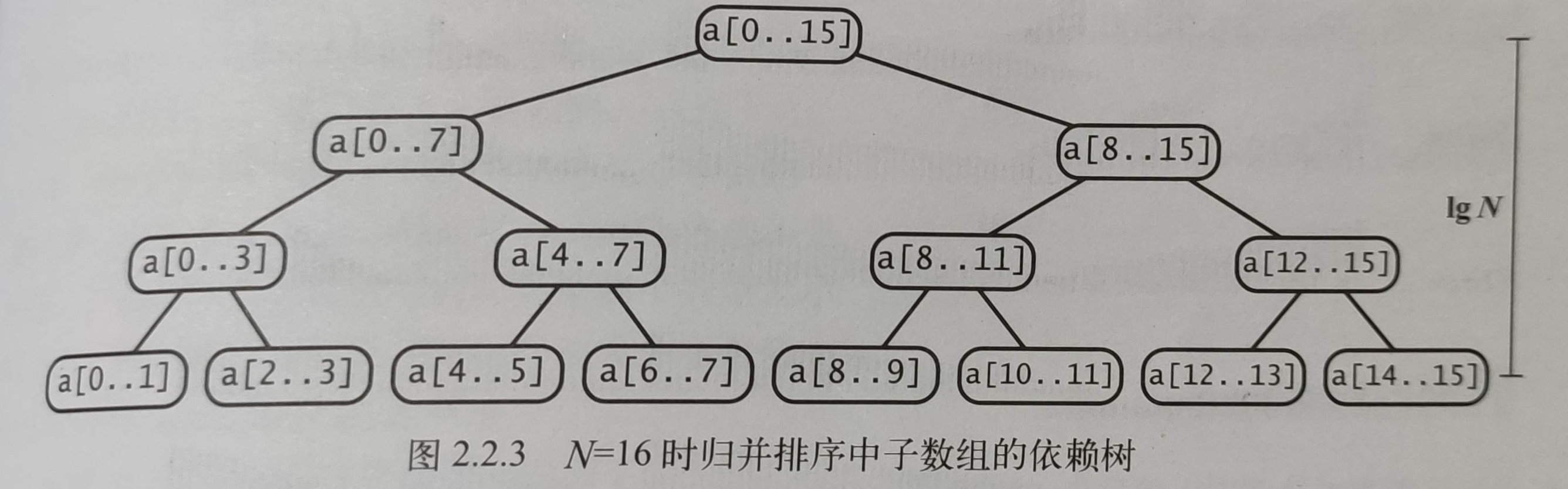
IMG_20210630_211627.jpg

  1. void mergesort(vector<int>&a){
  2.     vector<int>aux(a.size());
  3.     sort(a,0,a.size()-1,aux);
  4. }
  5. void sort(vector<int>& a,int lo,int ho,vector<int>& aux){
  6.     if (lo >= ho)return;
  7.     int mid = lo + (ho-lo)/2;//(ho+lo)/2的写法，防止lo+ho超过int
  8.     sort(a,lo,mid,aux);
  9.     sort(a,mid+1,ho,aux);
  10.     merge(a,lo,mid,ho,aux);
  11. }
  • 注意这里把辅助数组放在了参数列表里，而不作为merge()方法的局部变量，是为了避免每次递归归并时都会因新建数组而影响运行时间。所以可以把aux辅助数组作为sort()方法一次性只分配一次。

    void merge2(vector& a, int lo, int mid, int ho,vector& aux) {
    int i = lo, j = mid + 1;

    1.     for (int k = lo; k <= ho; k++)
    2.         aux[k] = a[k];
    3.    for (int k = lo; k <= ho; k++) {
    4.     //判定是否出界
    5.     if (i > mid)                    a[k] = aux[j++];//左半边已经遍历完
    6.     else if (j > ho)               a[k] = aux[i++];//右半边已经遍历完
    7.     else if (aux[j] <= aux[i]) a[k] = aux[j++];
    8.     else                              a[k] = aux[i++];
    9. }

    }

3.自底向上的归并排序

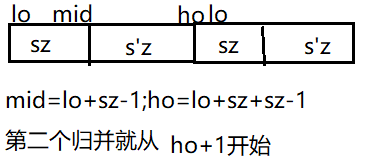
首先，进行两两归并（把每个元素想象成一个大小为1的数组），然后四四归并（将两个大小为2的数组归并），然后八八归并。。。在每一轮归并中，最后一次归并的第二个子数组可能比第一个子数组要小。

  1. void mergesortBU(vector<int>& a){
  2.     int n = a.size();
  3.     vector<int>aux(n);
  4.     for (int sz = 1;sz < n;sz += sz){//sz子数组大小
  5.         for (int lo = 0;lo < n-sz;lo = lo+sz+sz){//lo归并中第一个子数组的索引
  6.             merge(a,lo,lo+sz-1,min(lo+sz+sz-1,n-1),aux);
  7.             //lo+sz-1:归并中的mid,即第一次子数组的末尾;  ,min(lo+sz+sz-1,n-1)=ho归并中第二个子数组的末尾
  8.         }
  9.     }
  10. }

image.png
4.注意事项（结论）

  • 归并排序最坏下的比较次数和任意基于比较的排序算法所需的最少比较次数都是o(nlogn)。所以，在基于比较的排序算法下，不要寻求比归并更少的比较次数一般算法。
  • 对一般归并排序的性能改进:1.小数组使用插入排序 2.在merge()里添加判断，if(a[mid]<=a[mid+1])说明已经有序，无需再合并 3.为了节省在meger()中a[]复制到aux[]辅助数组的时间，每层的递归调用sort()时交换a[],aux[]的角色？？https://algs4.cs.princeton.edu/22mergesort/MergeX.java.html