选择排序

首先，找到数组中最小的那个元素，将它与第一个元素交换位置，其次，在剩下的元素中找到最小的与数组中第二个位置交换，如此往复，直至有序。因为其运行时间与输入的序列无关每次都要扫描一遍，而且数据的移动（交换）和数组大小呈线性关系。

  1. void selectsort(vector<int>& a){
  2.     int n = a.size();
  3.     for (int i = 0;i < n;i ++){
  4.         //将a[i] 和 a[i+1,...n-1]中元素交换
  5.         int min = i;
  6.         for (int j = i + 1;j < n;j ++)
  7.             if (a[j] < a[min] min = j;
  8.         swap(a[min],a[i]);
  9.     }
  10. }

插入排序（带交换操作）

把数组分成有序的左边和无序的右边，依次遍历右边元素，将其插入到左边的某个位置，左边有序的初始长度为1，直至整个数组都有序。

  1. void insertsort(vector<int>& a){
  2.     int n = a.size();
  3.     for (int i = 1;i < n;i ++){
  4.         //将ai插入到a[i-1],a[i-2],a[i-3]....之中
  5.         for (int j = i;j > 0 && a[j] <= a[j-1];j --)
  6.             swap(a[j],a[j-1]);//每一次a[j] <= a[j-1]就交换直至a[i]放到了左边中合适的位置
  7.     }
  8. }

特点：

  • 对于长度为n的数组：选择排序大约n²/2次比较和N次交换，插入排序大约n²/4次比较，n²/4次交换（互补重复下），最好情况n-1次比较，0次交换，最坏情况n²/2次，比较n²/2次交换。
  • 插入排序合适部分有序（每个元素距它的最终位置不远or一个有序大数组接小数组），小规模数组等情况。
  • 对于逆序数组，选择排序更快。因为选择排序需要进行N(N-1)/2次比较,N次交换。插入排序需要N(N-1)/2次比较，N(N-1)/2次交换。链接
  • 插入排序的交换操作与数组中倒置的数量相同，因为每次交换都改变了两个顺序颠倒的元素位置，相当于减少了一对倒置，当倒置数量为0时排序完成了。

  • 不要交换的插入排序

    1. void insertsort2(vector<int>& a){
    2.   int n = a.length();
    4.  // put smallest element in position to serve as sentinel
    5.   int exchanges = 0;
    6.   for (int i = n-1; i > 0; i--) {
    7.       if (a[i] <= a[i-1])) {
    8.           swap(a[i],a[i-1]);
    9.           exchanges++;
    10.       }
    11.   }
    12.   if (exchanges == 0) return;
    13.   //得到a[0]是最小元素，那么a[0],a[1]就暂时有序了
    14.   for (int i = 2; i < n; i++) { // insertion sort with half-exchanges
    15.       int v = a[i];
    16.       int j = i;
    17.       while (v <= a[j-1]) {
    18.           a[j] = a[j-1];
    19.           j--;
    20.       }
    21.       a[j] = v;
    22.   }
    23. }

    希尔排序

    1. public static void sort(Comparable[] a) {
    2.       int n = a.length;
    3.       // 3x+1 increment sequence:  1, 4, 13, 40, 121, 364, 1093, ... 
    4.       int h = 1;
    5.       while (h < n/3) h = 3*h + 1; 
    7.       while (h >= 1) {
    8.           // h-sort the array
    9.           for (int i = h; i < n; i++) {
    10.               for (int j = i; j >= h && less(a[j], a[j-h]); j -= h) {
    11.                   exch(a, j, j-h);
    12.               }
    13.           }
    14.           assert isHsorted(a, h); 
    15.           h /= 3;
    16.       }
    17. }

    各种排序算法的时间空间稳定性的比较

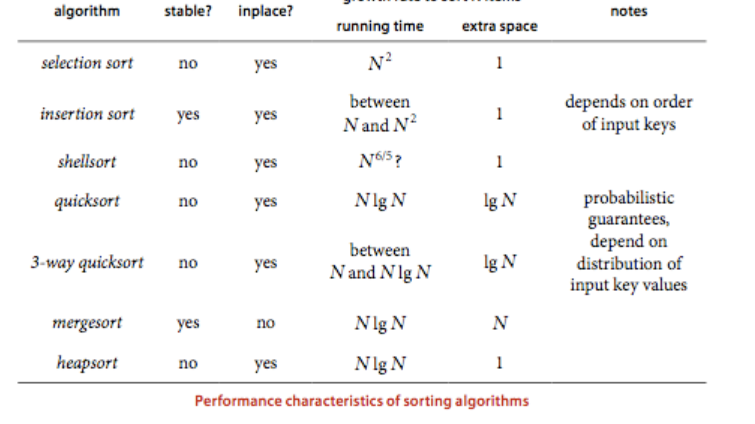
    image.png
    排序算法的应用

  • 找出重复元素，如果是暴力将所有元素都互相比较一遍，时间是平方级别，但是利用线性对数级的排序算法然后再遍历数组记录即可。

  • 中位数的查找和顺序统计。
  • 找到第k小的数。