优先队列的定义和应用

优先队列是一种抽象的数据类型，其最重要的是可以直接获取优先级最高的元素不必考虑具体实现，在一种堆排序的算法中，就是来源于基于堆的优先队列的的一种实现，通过插入一列一列元素，然后一个一个删除最大（小）的元素，优先队列最重要的操作是删除优先级最高的元素和插入方法（每次插入都会带来底层结构的变动，使优先级最高的永远在队头上）。
应用：试想在输入N数据量很庞大时，获得最小的M若干个元素，这时一是用排序算法先把输入量排序再一个一个引用其中的元素就显得非常不友好，排序时间会很长，甚至数据大到都无法装进内存里。还有一种思想是每个新的输入与已知的M个比较，时间复杂度O(M^N)。这时优先队列就应用而生。
优先队列的实现：

  • 数组实现（无序），insert()方法就是类似于栈的push();删除最大元素可以利用选择排序的内循环代码获取最大元素，然后将其与边界元素交换，删除即可。
  • 数组实现(有序），insert()方法类似于插入排序的移动操作；删除最大元素就直接删除边界类似于栈的pop();
  • 链表实现：构造一个逆序的链表即可

其实，优先队列中插入和删除的操作相比于栈或队列来说，它的操作时间是O(1),而栈或队列的时间是O(n）。

基于堆实现优先队列

1. 堆的定义

一颗二叉树的每个节点都 >= 它的两个孩子节点，则是堆有序的。

2. 二叉堆的表示法

我们可以用一个数组来表示二叉堆，即一棵完全二叉树，所以二叉堆是一个能够用堆有序的完全二叉树排序的元素，并在数组中按层级一次存储（不使用数组的第一个位置）。
在一个堆中，位置（索引）k的节点的父节点为向下取整（k/2），他的两个子节点分别是2k,2k+1。所以我们可以通过数组索引在树中上下移动。

3. 堆算法的实现

我们用长度为n+1的数组pq来表示一个大小为n的堆，不适用pq[0],pq[1…n]储存。

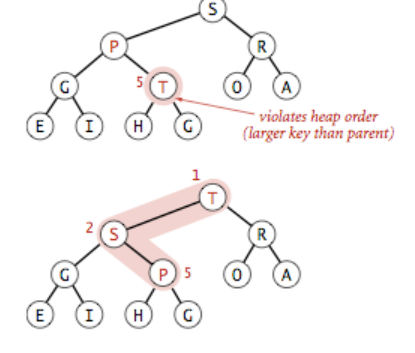
3.1上浮有序化

产生原因：在大顶堆来说，某个节点比它的父节点还大，需要交换它和它的父节点来使堆重新有序，但是交换后可能存在它仍然比交换后的父节点大，还需要进一步上浮直至遇上更大的父节点。

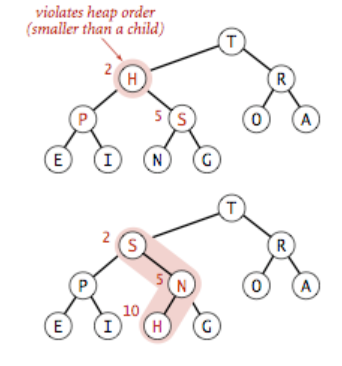
void swim(vector& a,int k){ while(k>1&& a[k/2] <= a[k]){ swap(a[k/2],a[k]); k=k/2; } } image.png

3.2 下沉有序化

产生原因：在大顶堆来说，某个节点变得比它的两个子节点或其中之一更小而打破了堆有序的状态。需要交换它和它的两个子节点中较大的来使堆重新有序，但是交换后可能还是比它的子节点小，不断向下移动直至达到了堆的底部或是它的子节点都比它小。

void sink(vector& a, int k, ing n){//n表示此时堆的大小 while(2k<=n）{ int j = 2k; if (j < n && a[j] <= a[j+1]) j++;//右字节点更大 if (a[k] >= a[j]) break;//无需操作，相等的话也不会会 swap(a[k],a[j]);// k = j;//继续下沉 } }

image.png

3.3 基于堆的插入，删除最大操作

  • 将新元素加到数组末尾并同时堆大小加1，然后swim(n）到合适的位置。
  • 从数组的顶端（这里是pq[1]）删除最大元素，但是要从大顶堆的的pq[n]逻辑删除，所以要先与头部交换，再n—。

    void insert(int v){ pq[++n] = v; swim(n); } void delmax(){ int max = pq[1]; swap(a[1],a[n]); n—; sink(1); return max; }

以上代码在实现上可能有出入。

堆排序

给输入数据升序排序时，将所有元素插入，然后重复调用优先队列的删除最小元素操作来依次获取从小到大的数组。用无序数组实现的优先队列其实就是选择排序，那么，基于堆的排序分为——堆的构造和下沉sink排序两个阶段，最后在堆中按递减顺序取出所有元素得到排序结果。（这里因为在大顶堆中，pq[1]是最大元素，但是删除操作是先把pq[1]与pq[n]调换，sink(1),再逻辑上n—表示堆中pq[n]已经删除，但物理上还是存在的）

堆构造阶段和下沉排序阶段

在堆排序时，需要排序的数组本身作为堆来使用并直接使用swim(),sink()。两种方法构造。

  1. 逐个插入。从左到右遍历数组，用swim()操作保证扫描指针左侧的所有元素已经是堆有序了，连续插入到堆中。

在构造好一个堆有序的数组后，开始进行数组的排序——把pq[1]与pq[n—]交换，然后sink(1)操作直至n==1为止。

  1. void swim(vector<int>& pq,int k) {
  2.     while (k > 1 && pq[k / 2] < pq[k]) {
  3.         swap(pq[k / 2], pq[k]);
  4.         k = k / 2;
  5.     }
  6. }
  7. void insert(vector<int>& pq, int k,int N) {
  8.     pq[++N] = k;
  9.     swim(pq,N);
  10. }
  11. void sink(vector<int>& b, int k, int n) {
  12.     //大顶堆下沉
  13.     while (2 * k <= n) {
  14.         int j = 2 * k;
  15.         if (j < n && b[j] <= b[j + 1])j++;
  16.         if (b[k] >b[j]) break;//不用交换
  17.         swap(b[k], b[j]);
  18.         k = j;
  19.     }
  20. }
  21. void heap_sort(vector<int>& a) {
  22.     int n = a.size();
  23.     vector<int>pq(n + 1);
  24.     for (int i = 0; i < n; i++) insert(pq,a[i],i);//构造了一个堆有序
  26.     while (n > 1) {
  27.         swap(pq[1], pq[n--]);
  28.         sink(pq, 1,n);
  29.     }
  30.     for (int i = 0; i < a.size(); i++) a[i] = pq[i + 1];
  31. }

  1. 由底向上把待排序的数组看成已经是一个堆了，每个元素是一个个堆有序的子数组，只差把它构造成整个堆有序的完全二叉树了。利用sin()从N/2的位置递减操作直至位置为1结束。

    1. void sink(vector<int>& b, int k, int n) {
    2.  //大顶堆下沉
    3.  while (2 * k <= n) {
    4.      int j = 2 * k;
    5.      if (j < n && b[j] <= b[j + 1])j++;
    6.      if (b[k] >b[j]) break;//不用交换
    7.      swap(b[k], b[j]);
    8.      k = j;
    9.  }
    10. }
    11. vector<int> heap_sort(vector<int>& a) {
    12.  int n = a.size();
    13.  vector<int>b(n + 1);
    14.  for (int i = 0; i < n; i++) b[i + 1] = a[i];
    16.  for (int k = n / 2; k >= 1; k--) 
    17.      sink(b, k,n);
    19.  while (n > 1) {
    20.      swap(b[1], b[n--]);//每次把最大元素
    21.      sink(b, 1, n);
    22.  }
    23.  //n发生了变化，不再是数组a的大小，而是逻辑上堆结构的大小
    24.  for (int i = 0; i < a.size(); i++) a[i] = b[i + 1];
    25.  return a;
    26. }

    堆排序的过程展示
    总结：两种方法的构造堆中sink()下沉排序是相同的思想，都是把堆顶pq[1]与堆的末尾交换并使堆的逻辑大小减一，在sink(1）。

    互动问题

  2. 为什么在堆的表示中不使用pq[0]?

为了简化表达和计算。如果是pq[0]的话，就不符合上面的二叉树索引表示父子节点关系的式子。pq[0]的子节点是pq[1],pq[2]。

  1. 在我看来，逐个添加元素到堆中的的构造方法一比从数组的一半开始由底向上构造简单，但为什么推荐第二种？

因为第二种的时间更快，而且更简洁（不用swim()）。

  1. 堆其实就是一颗完全二叉树，那么一颗大小为N的二叉树高度为向下取整（lgN)。