1. **有个文章很不错**[**尊重原创，转载地址，侵权告删。**](https://www.cnblogs.com/skywang12345/p/3245399.html)<br />对于二叉查找树来说，最好的情况是高度平衡时，最坏的情况是线性查找，而且在插入和删除中保持二叉树的完美平衡大代价太高，由此引入了一种2-3查找树。

1. 2-3查找树

在二叉查找树中，一个节点有一个键两条链接，称为2-结点。为此，引入3-结点（两个键，3条链接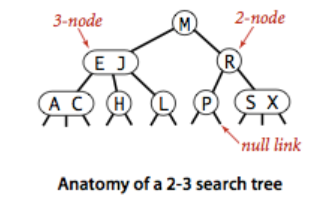）image.png
现在对这课2-3查找树进行查找，插入，删除等操作的解释。

1.1查找

与二叉查找树类似，递归的往下查找元素，直至命中或者所查链接为空（不命中）为止。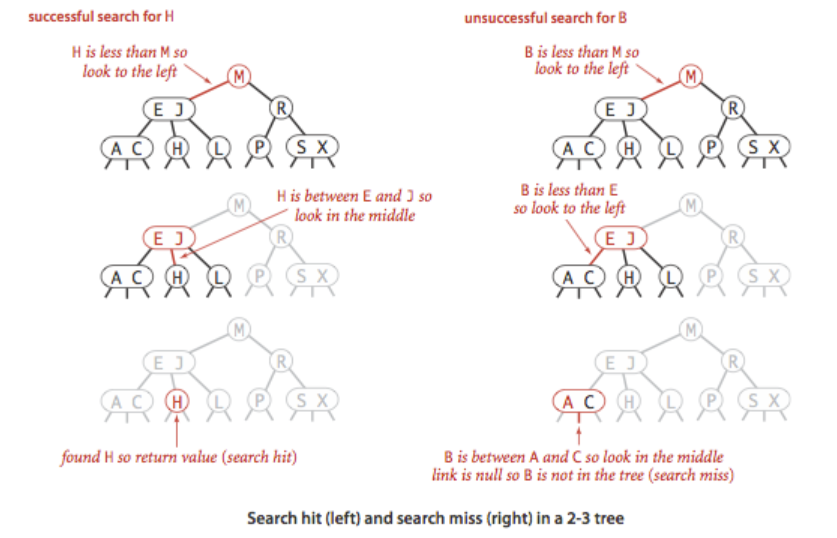
image.png

1.2 插入

  • 1.2.1 向2-结点插入新键就会变成3-结点。比如当未命中的查找结束于一个2-结点时，直接将其替换成3-结点。
  • 1.2.2 向3-结点插入新键，需要变形。这里我们先将新键存入该结点，使3-结点变成一个临时的4-结点，再将它转化成3个2-结点（把中间大小的键作为左右两结点的父节点即可）。

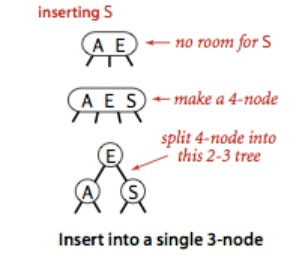
image.png

  • 1.2.3 向一个父节点为2-结点的3-结点插入新键。与上面类似，先将新键与3-结点结合成一个临时的4-结点，将4-结点分解出一个中间大小的键给父节点，让父节点变成3-结点。

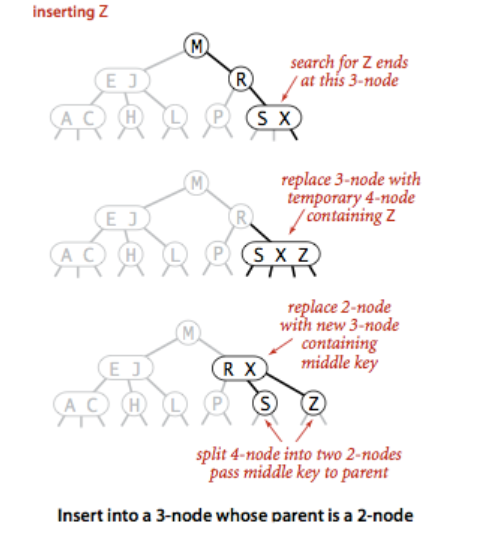
image.png

  • 1.2.4 向一个父节点为3-结点的3-结点中插入新键。与1.2.3类似，只不过父节点还有继续往上分解直至到根节点或变成一个合格的3-结点/2-结点。

总结：在插入时可能需要分解4-结点，所以有如下几种情况：

2. 红黑二叉查找树

因为2-3查找数在实现上需要维护两种不同的结点，此外不同结点之间还有相互转化，处理的情况太多，因此不易于实现。而且，2-3树的存在就是为了消除二叉查找树中存在的较坏的情况，我们可以引入红黑树。

1.红黑树的定义

红链接将两个2-结点连起来，形成逻辑上的3-结点。其实，把红链接压平，就变成一棵2-3树。 黑链接是普通链接。（在实现上，可以把指向结点上的链接颜色存入自己的结构体内） 红链接都是左连接。 任何一个结点都不能同时和两条红链接相连。 任意空链接到根节点上的路径中黑链接数量相同。

另一种广泛的表达：

（1）每个节点或者是黑色，或者是红色。
（2）根节点是黑色。
（3）每个叶子节点（NULL）是黑色。 [注意：这里叶子节点，是指为空(NIL或NULL)的叶子节点！]
（4）如果一个节点是红色的，则它的子节点必须是黑色的。
（5）从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。

2 旋转

在某些操作时会使出现与红黑树的定义不符合的情况，此时需要旋转来修复，旋转会改变红链接的指向。左旋和右旋都会返回一个原来父节点的链接颜色。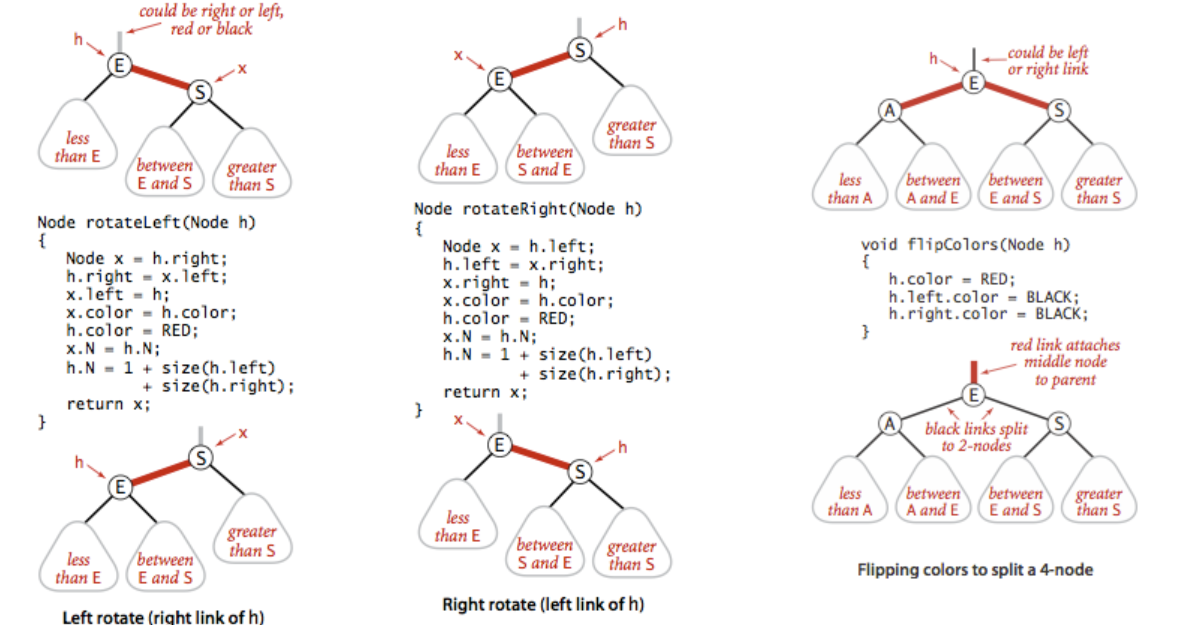
image.png

3 插入操作

为了保持有序性，都是用红链接将新节点和它的父节点相连。此时，可能插入后有了一个红色的右链接，需要一次左旋转。

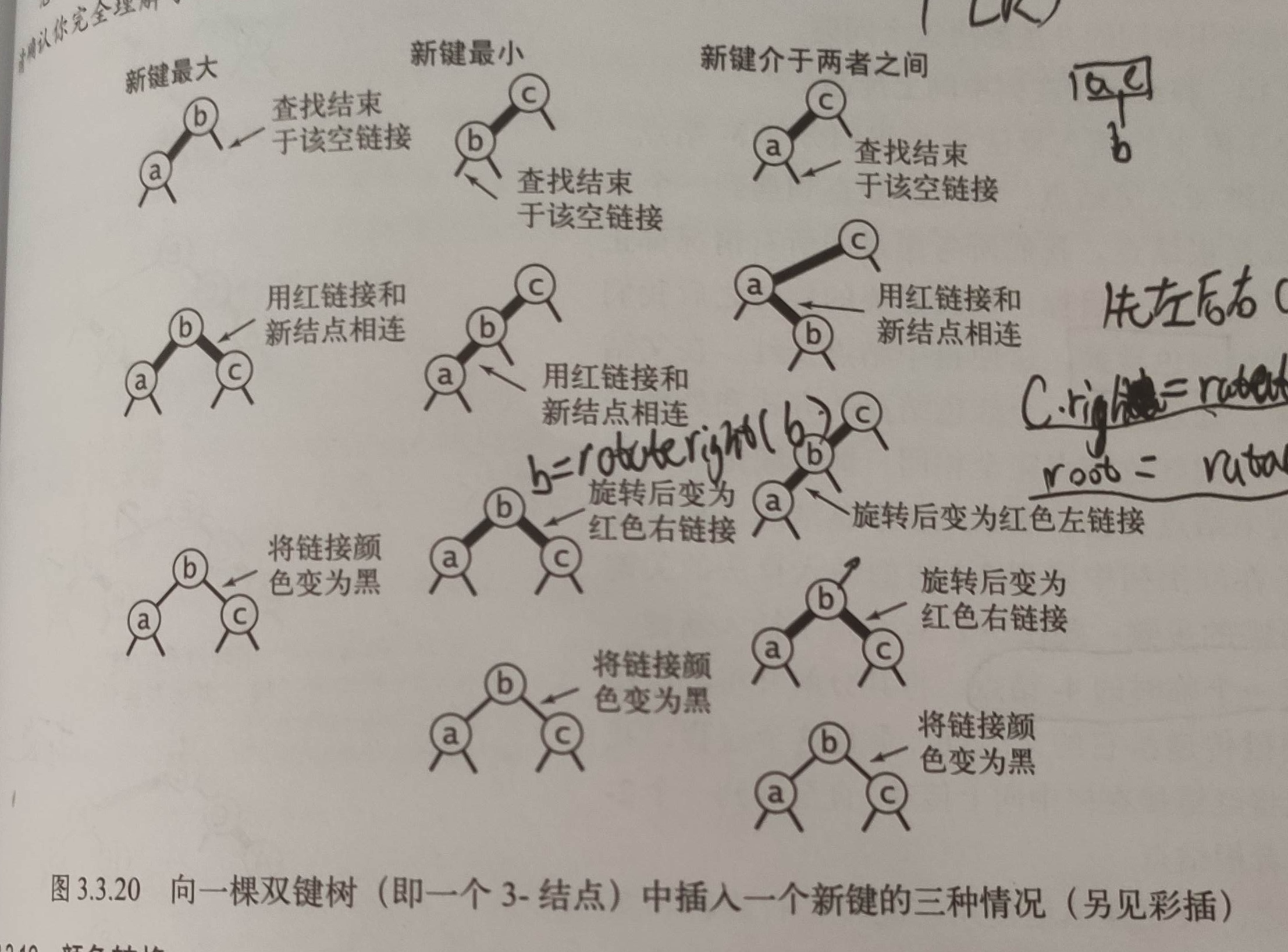
  • 向一颗双键（3-结点）树插入新结点可能存在一下变化。
  • （颜色转换，当父节点连接的两个子节点的链接都是红色，都要变成黑色，红链接被传给父节点了）

1625819205368.jpg

  • 向底部的3-结点插入新键，情况与上面类似，但是红色链接需要一步步向上传递。
  • 当发生颜色转换时，根节点可能会变成红色，但是红色的根节点说明它是3-结点的一部分，但是事实并非如此，所以每次插入后需要检查根节点是不是黑色的。

    总结

  1. 若右子节点是红色而左子节点是黑色，左旋转。
  2. 若左子节点和右子节点都是红色，颜色转换。
  3. 若连续两个左子节点都是红色，右旋转。

    4. 删除操作

    （目前还没有看懂。。。。）