题外话:STL中的sort()源码就有下面类似的快排知识——https://feihu.me/blog/2014/sgi-std-sort/
- 快排思想:
一种基于分治的排序算法,将数组分成两个子数组,并对子数组独立排序,当两个子数组有序后整个数组自然有序,与归并排序类似但有区别。
快排算法:
先切分处pos枢纽,再左右两边递归快排。
写法一:int partition(vector<int>& a, int l, int r) {//划分数组int priovt = a[l];int i = l, j = r + 1;//注意:l...r划分,但每次比较的是a[++i],a[--j]//使得a[i]<=priovt<=a[j]while (1) {while (a[++i] <= priovt)if (i == r) break;while (a[--j] >= priovt)if (j == l)break;if(i >= j)break;swap(a[i], a[j]);}swap(a[l], a[j]);return j;//因为最后跳出循环的是i>=j;而此时a[j]<=priovt<=a[i]的,//并且作为priovt的a[l]没动,所以最后交换a[l],a[j]}void quicksort(vector<int>& a, int l, int r) {if (l >= r) return;//终止循环int pos = partition(a, l, r);quicksort(a, l, pos - 1);quicksort(a, pos + 1, r);}void sort(vector<int>& a) {int n = a.size();quicksort(a, 0, n - 1);}
写法二:(带哨兵)
void quicksort1(vector<int>& b,int l,int r) {if (l >= r) return;//种植递归int i = l, j = r;int temp = b[l];while (i != j) {//顺序很重要,因为基准是最左边,先要从右往左比较while (i != j && b[j] > temp)j--;while(i != j && b[i] <= temp)i++;//跳出上面两个循环的条件是 查到了不符合大小的元素if (i != j) swap(b[i], b[j]);}//i==j 获得基准ib[l] = b[i];b[i] = temp;//递归快排quicksort(b, l, i - 1);quicksort1(b, i + 1, r);}void sort1(vector<int>& b) {int n = b.size();quicksort(b, 0, n - 1);}
注意事项
- 别越界:如果切分元素是数组中最小或最大的元素,别让扫描指针跑出数组边界。另外注意考虑到还存在与枢纽相同的元素而导制切分失败,
- 保持随机性:即随机切分一个元素(指定一个枢纽)
- 考虑到有重复的元素时,以上快排算法可能会有不必要的等值元素交换,所以推荐“三向切分的快排”
- 递归中止:当切分元素不能放入正确的位置时,导致切分元素正好是子数组的最大最小值陷入了无限递归。
- 算法改进
1.首先,明确快排适合于不是基本有序的,大数组情况,而对于小数组,快排比插入排序慢,这时可以切换到插入排序,具体的M一般选取5~15.
修改如下:
void quicksort(vector<int>& a, int l, int r) {if (l >= r) return;//终止循环/*************/if (l + m >= h) {insertsort(a,l,h);return ;}/************/int pos = partition(a, l, r);quicksort(a, l, pos - 1);quicksort(a, pos + 1, r);}
2.**三向切分快排:适用于重复元素较多的情况,能将O(Onlogn)降到O(n)级别**<br />因为有较多重复元素,所以相比一般快排,采取三个指针来维护数组,lt使a[lo...lt-1]都小于privot;gt使得a[gt+1..h]都大于privot,指针i使a[lt...i-1]都等于privot。a[i...gt]还未确定。<br />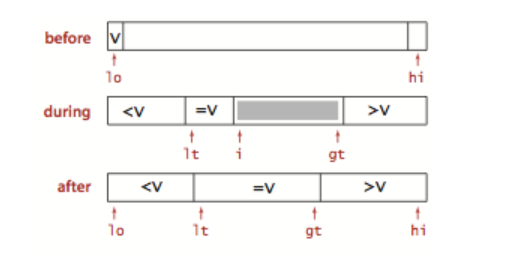<br />初始时i=lo+1,lt=lo,gt=h,对a[i]与privot比较
- a[i] < privot 交换a[lt],a[i] , lt++;i++;
- a[i] > privot 交换a[gt],a[i],gt—;
- a[i] = privot i++;
3.三取样切分快排:因为上述的一般快排是把最左边的元素作为切分点(枢纽),然而可以选取部分小数组的中位数作为切分元素,但是计算中位数代价也许更高,这时可以用前三个元素(取样大小=3)的小数组中计算中位数而作为枢纽效果最好。 ```java //返回三取样切分元素索引 private static int ThreeMedianIndex(Comparable[] a,int lo,int hi) {void quicksort3way(vector<int>& a,int l,int h){if (l >= h) return ;//递归种植int i = l+1;lt=l,gt=h;int privot = a[l];while(i<=gt){if(a[i]<privot){swap(a[i++],a[lt++]);}else(a[i] > privot){swap(a[i],a[gt--])}else i++;}quicksort3way(a,l,lt-1);quicksort3way(a,gt+1,h);}
}//子数组少于3个元素时,第一个元素作为切分元素if((hi-lo+1)<3) return lo;//子数组有3个或以上元素时,取子数组前三个元素的中位数作为切分元素////将原数组的前三个元素的索引作为新数组的值Integer[] b={lo,lo+1,lo+2};////使用插入排序法排序新数组b,按原数组的值进行排序。排序后的结果是原数组中小中大值对应的索引for(int i=0;i<2;i++)for(int j=i+1;j>0;j--)if (less(a[b[j]],a[b[j-1]])) exch(b,j,j-1);return b[1];
private static int partition(Comparable[] a,int lo,int hi) { int i=lo,j=hi+1; int newVIndex=ThreeMedianIndex(a,lo,hi); exch(a,lo,newVIndex); Comparable v=a[lo]; while(true) { while(less(a[++i],v)) if(i==hi) break; while(less(v,a[—j])) if(j==lo) break;
if(i>=j) break;exch(a,i,j);}exch(a,lo,j);return j;}
链接[链接](https://www.cnblogs.com/longjin2018/p/9860246.html)3. 应用:寻找第K小的元素;如果是第K大,可以第n-K+1小来算。```cppint select(vector<int>&a,int k){int l = 0,r = n-1;while(l<r){int pos = partition(a,l,r);//pos是整个数组的索引if(pos == k-1) return a[pos];else if(pos > k-1) r=pos-1;else l=pos+1;}//当l >= r时,说明虽然没有找到pos=k-1但是a[]已经有序了,直接返回return a[k-1];}

