1、上溢和下溢

在数字计算机上实现连续数学的基本困难是：我们需要通过有限数量的位模式来表示无限多的实数，这意味着我们在计算机中表示实数时几乎都会引入一些近似误差。在许多情况下，这仅仅是舍入误差。如果在理论上可行的算法没有被设计为最小化舍入误差的累积，可能会在实践中失效，因此舍入误差是有问题的，特别是在某些操作复合时。

一种特别毁灭性的舍入误差是下溢。当接近零的数被四舍五入为零时发生下溢。许多函数会在其参数为零而不是一个很小的正数时才会表现出质的不同。例如，我们通常要避免被零除。

另一个极具破坏力的数值错误形式是上溢 (overflow)。当大量级的数被近似为
或
时发生上溢。进一步的运算通常将这些无限值变为非数字。

必须对上溢和下溢进行数值稳定的一个例子是softmax 函数。softmax 函数经常用于预测与 multinoulli 分布相关联的概率，定义为：

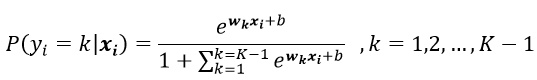
softmax 函数在多分类问题中非常常见。这个函数的作用就是使得在负无穷到 0 的区间趋向于 0，在 0 到正无穷的区间趋向于 1。上面表达式其实是多分类问题中计算某个样本
的类别标签
属于 K 个类别的概率，最后判别
所属类别时就是将其归为对应概率最大的那一个。

当式中的
都是很小的负数时，
就会发生下溢，这意味着上面函数的分母会变成 0，导致结果是未定的；同理，当式中的
是很大的正数时，
就会发生上溢导致结果是未定的。

5-2、计算复杂性与 NP 问题

1、算法复杂性

现实中大多数问题都是离散的数据集，为了反映统计规律，有时数据量很大，而且多数目标函数都不能简单地求得解析解。这就带来一个问题：算法的复杂性。

算法理论被认为是解决各类现实问题的方法论。衡量算法有两个重要的指标：时间复杂度和空间复杂度，这是对算法执行所需要的两类资源——时间和空间的估算。

一般，衡量问题是否可解的重要指标是：该问题能否在多项式时间内求解，还是只能在指数时间内求解？在各类算法理论中，通常使用多项式时间算法即可解决的问题看作是易解问题，需要指数时间算法解决的问题看作是难解问题。

指数时间算法的计算时间随着问题规模的增长而呈指数化上升，这类问题虽然有解，但并不适用于大规模问题。所以当前算法研究的一个重要任务就是将指数时间算法变换为多项式时间算法。

2、确定性和非确定性

除了问题规模与运算时间的比较，衡量一个算法还需要考虑确定性和非确定性的概念。

这里先介绍一下“自动机”的概念。自动机实际上是指一种基于状态变化进行迭代的算法。在算法领域常把这类算法看作一个机器，比较知名的有图灵机、玻尔兹曼机、支持向量机等。

所谓确定性，是指针对各种自动机模型，根据当时的状态和输入，若自动机的状态转移是唯一确定的，则称确定性；若在某一时刻自动机有多个状态可供选择，并尝试执行每个可选择的状态，则称为非确定性。

换个说法就是：确定性是程序每次运行时产生下一步的结果是唯一的，因此返回的结果也是唯一的；非确定性是程序在每个运行时执行的路径是并行且随机的，所有路径都可能返回结果，也可能只有部分返回结果，也可能不返回结果，但是只要有一个路径返回结果，那么算法就结束。

在求解优化问题时，非确定性算法可能会陷入局部最优。

3、NP 问题

有了时间上的衡量标准和状态转移的确定性与非确定性的概念，我们来定义一下问题的计算复杂度。

P 类问题就是能够以多项式时间的确定性算法来对问题进行判定或求解，实现它的算法在每个运行状态都是唯一的，最终一定能够确定一个唯一的结果——最优的结果。

NP 问题是指可以用多项式时间的非确定性算法来判定或求解，即这类问题求解的算法大多是非确定性的，但时间复杂度有可能是多项式级别的。

但是，NP 问题还要一个子类称为NP 完全问题，它是 NP 问题中最难的问题，其中任何一个问题至今都没有找到多项式时间的算法。

机器学习中多数算法都是针对 NP 问题（包括 NP 完全问题）的。

5-3、数值计算

上面已经分析了，大部分实际情况中，计算机其实都只能做一些近似的数值计算，而不可能找到一个完全精确的值，这其实有一门专门的学科来研究这个问题，这门学科就是——数值分析（有时也叫作 “计算方法”）；运用数值分析解决问题的过程为：实际问题→数学模型→数值计算方法→程序设计→上机计算求出结果。

计算机在做这些数值计算的过程中，经常会涉及到的一个东西就是“迭代运算”，即通过不停的迭代计算，逐渐逼近真实值（当然是要在误差收敛的情况下）。

2、几种常用的距离

上面大致说过， 在机器学习里，我们的运算一般都是基于向量的，一条用户具有 100 个特征，那么他对应的就是一个 100 维的向量，通过计算两个用户对应向量之间的距离值大小，有时候能反映出这两个用户的相似程度。这在后面的 KNN 算法和 K-means 算法中很明显。

2.1、 闵可夫斯基距离

闵可夫斯基距离（Minkowski distance）是衡量数值点之间距离的一种非常常见的方法，假设数值点 P 和 Q 坐标如下：

那么，闵可夫斯基距离定义为：

假设在曼哈顿街区乘坐出租车从 P 点到 Q 点，白色表示高楼大厦，灰色表示街道：

绿色的斜线表示欧几里得距离，在现实中是不可能的。其他三条折线表示了曼哈顿距离，这三条折线的长度是相等的。

曼哈顿距离(P=1)
曼哈顿距离也称为城市街区距离，数学定义如下：


欧氏距离(P=2)
欧氏距离其实就是 L2 范数，数学定义如下：

切比雪夫距离(P=∞)：

我们知道平面上到原点的欧几里得距离（p = 2）为 1 的点所组成的形状是一个圆，当 p 取其他数值的时候呢？

注意，当 p < 1 时，闵可夫斯基距离不再符合三角形法则，举个例子：当 p <1,时，点(0,0) 到点 (1,1) 的距离等于 >2 ,到这两个点的距离都是 1。

闵可夫斯基距离比较直观，但是它与数据的分布无关，具有一定的局限性，如果 x 方向的幅值远远大于 y 方向的值，这个距离公式就会过度放大 x 维度的作用。所以，在计算距离之前，我们可能还需要对数据进行 z-transform 处理，即减去均值，除以标准差：

: 该维度上的均值
: 该维度上的标准差

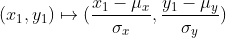
2.2、 马氏距离

马氏距离实际上是利用 Cholesky transformation 来消除不同维度之间的相关性和尺度不同的性质。假设样本点（列向量）之间的协方差对称矩阵是 ， 通过 Cholesky Decomposition可以转化为下三角矩阵和上三角矩阵的乘积： 。消除不同维度之间的相关性和尺度不同，只需要对样本点 x 做如下处理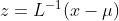： 。处理之后的欧几里得距离就是原样本的马氏距离：为了书写方便，这里求马氏距离的平方：

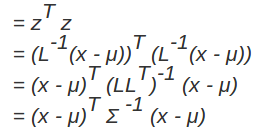
故马氏距离为

2.3、向量内积

夹角余弦的取值范围为[-1,1]，可以用来衡量两个向量方向的差异；夹角余弦越大，表示两个向量的夹角越小；当两个向量的方向重合时，夹角余弦取最大值 1；当两个向量的方向完全相反时，夹角余弦取最小值 - 1。
机器学习中用这一概念来衡量样本向量之间的差异，其数学表达式如下：

2.4、字符串距离

汉明距离
汉明距离（Hamming distance）是指，两个等长字符串 s1 与 s2 之间的汉明距离定义为将其中一个变为另外一个所需要作的最小替换次数

信息编码中一般应使得编码间的汉明距离尽可能的小。

编辑距离
编辑距离是指两个字串之间（不用等长），由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。编辑距离求的是最少编辑次数。很多，略

2.5、相似性的评估

杰卡德相似系数
两个集合 A 和 B 的交集元素在 A 和 B 的并集中所占的比例称为两个集合的杰卡德相似系数，用符号 J(A,B) 表示，数学表达式为：

杰卡德相似系数是衡量两个集合的相似度的一种指标。一般可以将其用在衡量样本的相似度上。

在一些情况下，某些特定的值相等并不能代表什么。举个例子，用 1 表示用户看过该电影，用 0 表示用户没有看过，那么用户看电影的的信息就可用 0,1 表示成一个序列。考虑到电影基数非常庞大，用户看过的电影只占其中非常小的一部分，如果两个用户都没有看过某一部电影（两个都是 0），并不能说明两者相似。反而言之，如果两个用户都看过某一部电影（序列中都是 1），则说明用户有很大的相似度。在这个例子中，序列中等于 1 所占的权重应该远远大于 0 的权重，这就引出下面要说的杰卡德相似系数（Jaccard similarity）。

在上面的例子中，用 M11 表示两个用户都看过的电影数目，M10 表示用户 A 看过，用户 B 没看过的电影数目，M01 表示用户 A 没看过，用户 B 看过的电影数目，M00 表示两个用户都没有看过的电影数目。Jaccard 相似性系数可以表示为：

杰卡德距离
与杰卡德相似系数相反的概念是杰卡德距离，其定义式为：