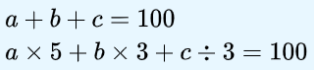image.png

一：暴力-蛮力：百钱百鸡、趣味题

概述

蛮力法(brute force method, BF)，是一种简单直接地解决问题的方法，常常直接基于问题的描述和所涉及的概念定义。通常蛮力策略也常常是最容易实现的方法。

使用蛮力法求解，必须要找出所有可能的情况，然后对每一种情况试探是否为所求。蛮力法需要对数据进行扫描或对问题解空间进行遍历，确保对每一个元素都访问且只访问一次（既不要遗漏，也不要重复） ，从而找出问题的解。

常见的遍历技巧：
数组、集合、线性表、链接表、栈、队列的遍历
子集的遍历
树、图的遍历
组合的遍历
排列的遍历

优缺点
虽然巧妙和高效的算法很少来自于蛮力法，但它在算法设计策略中仍然具有重要地位。

  1. 蛮力法适应能力强，是唯一一种几乎什么问题都能解决的一般性方法。
  2. 蛮力法一般容易实现，在问题规模不大的情况下，蛮力法能够快速给出一种可接受速度下的求解方法。
  3. 虽然通常情况下蛮力法效率很低，但可以作为衡量同类问题更高效算法的准绳。


典型应用：

  • 查找问题：顺序查找、串匹配问题
  • 排序问题：选择排序、冒泡排序
  • 组合问题：任务指派问题（全排列）、0/1 背包问题（幂集）
  • 图问题：哈密顿回路（顶点排列）
  • 几何问题：最近点对、凸包问题

    问题1：百钱百鸡问题

    公元 5 世纪末，中国古代数学家张丘建在《算经》中提出一个问题
    意思是公鸡每只 5 元、母鸡每只 3 元、小鸡 3 只 1 元，用 100 元买 100 只鸡，求公鸡、母鸡、小鸡的只数。
    image.png
    解法一（三重循环）

    1.采用穷举法，可能买到的公鸡数从 0 到 19 只,母鸡数从 0 到 33 只,小鸡数从 0 到 100 只。 2.c%3==0 ！！易忘 采用三重循环来遍历全部组合，运算步骤上万步。 

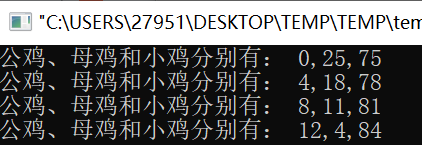
  1. #include <stdio.h>
  2. int main() {
  3.     int a,b,c;//公鸡、母鸡、小鸡
  4.     for (a=0; a<20; a++) {
  5.         for (b=0; b<34; b++) {
  6.             for (c=0; c<100; c++) {
  7.                 if ((a+b+c==100)&&(5*a+3*b+c/3==100)&&(c%3==0)) {
  8.                     printf("公鸡、母鸡和小鸡分别有：%d,%d,%d\n",a,b,c);
  9.                 }
  10.             }
  11.         }
  12.     }
  13. }

解法二（二重循环）

解法一(三重循环)情况数目很大， 需优化。
1.由于先a后b，故b循环时可以b<(100-a*5)/3
2.另外 c=100-a-b。我们可以通过 c=100-a-b 这条已知条件，减去一个循环， 使算法复杂法降为 N 的平方，运算步骤减至几百步。 

  1. #include <stdio.h>
  2. int main(){
  3.     int a,b,c;
  4.     for (a=0;a<20;a++){
  5.         for (b=0;b<(100-a*5)/3;b++) {
  6.             c = 100-a-b;
  7.             if ((5*a+3*b+c/3==100)&&(c%3==0)) {
  8.                     printf("公鸡、母鸡和小鸡分别有： %d,%d,%d\n",a,b,c);
  9.             }
  10.         }
  11.     }
  12. }

解法三（一重循环）

1.已知方程组image.pngimage.png故可只用一重循环来确定公鸡的数量 2.根据 b=(25-7*c/a)>=0,得出 a 小于 15 image.png

  1. #include <stdio.h>
  2. int main() {
  3. int a,b,c; //定义变量公鸡，母鸡，小鸡
  4.     for(a=0; a<15; a++) { //根据 b=(25-7*c/a)>=0,得出 a 小于 15
  5.         b=25-a*7/4.0;
  6.         c=75+a*3/4.0;
  7.         if (b>=0 && c>=0 && c%3==0 && a+b+c==100)
  8.              printf("公鸡、母鸡和小鸡分别有： %d,%d,%d\n",a,b,c);
  9.     }
  10.     return 0;
  11. }

问题2.趣味题-犯罪问题

问题描述：警察局抓住了 A、B、C、D 四名盗窃嫌疑犯，其中只有一人是小偷。
在审问时 image.png
现在已经知道这四人中有三人说的是真话，一人说的是假话。请问到底谁是小偷？ 

  1. #include <stdio.h>
  2. int main(void) {
  3.     int a,b,c,d;
  4.     for(a=0;a<=1;a++) //1 代表小偷 0 代表不是小偷
  5.         for(b=0;b<=1;b++)
  6.             for(c=0;c<=1;c++)
  7.                 for(d=0;d<=1;d++)
  8.                     if(!a+c+!d+d==3 && a+b+c+d==1)
  9.                           printf("A:%d B:%d C:%d D:%d",a,b,c,d);
  10. }

!a+c+!d+d==3这里不太理解

1.硬币兑换问题
问题描述：用 100 元面值的纸币兑换成面值 1 元、2 元和 5 元硬币，有多种不同的兑换方法，请输出所有可能的方案。

  1. #include <stdio.h>
  2. int main() {
  3.     int a,b,c;                 //5元、2元、1元
  4.     int count = 0;
  5.     for (a=0;a<=20;a++) {
  6.         for (b=0; b<=(100-5*a)/2; b++) {
  7.             for (c=0; c<=(100-5*a-2*b); c++) {
  8.                 if ((5*a+2*b+1*c)==100) {
  9.                   count++;
  10.                     printf("1元、2元和5元分别有：%d,%d,%d,一共%d种可能\n",c,b,a,count);
  11.                 }
  12.             }
  13.         }
  14.     }
  15. }

小问题：for (b=0; b<50; b++) 改为 for (b=0; b<(100-5*a)/2; b++) image.png image.png 受到上面百钱百鸡的影响，没有加等号


2.零件问题
问题描述：有一堆零件,(100-200 个之间),如果以四个零件为一组,则多 2 个零件,如果以 7 个零件为一组进行分组,则剩 3 个零件，如果以 9 个零件为一组，则剩 5 个零件。请问零件一共有多少？请输出所有可能的方案。
3.啤酒饮料问题
问题描述：啤酒每罐 2.3 元，饮料每瓶 1.9 元，小明买了若干饮料喝啤酒，总共花了 82.3 元，并且他买的啤酒的数量比饮料的少，请问他买了多少罐啤酒和多少瓶饮料。请输出所有可能的方案。
4.污损数字问题
有等式[■×(■3+■)]²=8■■9，其中■处为 1 个数字，滴上了墨水无法辨认。请编程找出■表示哪些数字， 输出整个等式。
5.委派任务
某侦察队接到一项紧急任务，要求在 A、B、C、D、E、F 六个队员中尽可能多地挑若干人，但有以下限制条件：
 A 和 B 两人中至少去一人；
 A 和 D 不能一起去；
 A、E 和 F 三人中要派两人去；
 B 和 C 都去或都不去；
 C 和 D 两人中去一个；
 若 D 不去，则 E 也不去。
输出结果如下：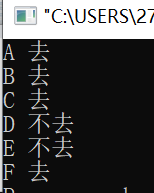
image.png

  1. #include <stdio.h>
  2. int main() {
  3.     int a,b,c,d,e,f;
  4.     for (a=0; a<=1; a++)       //1 代表去 0 代表不去
  5.         for (b=0; b<=1; b++)
  6.             for (c=0; c<=1; c++)
  7.                 for (d=0; d<=1; d++)
  8.                     for (e=0; e<=1; e++)
  9.                         for (f=0; f<=1; f++)
  10.                         {
  11.                             if (d == 0)
  12.                                 e = 0;
  13.                             if (a+b>=1 && a+d == 1 && a+e+f == 2 && (b+c==0 || b+c==2) && c+d==1)
  14.                             {
  15.                                 if(a==1) printf("A 去\n"); else printf("A 不去\n");
  16.                                 if(b==1) printf("B 去\n"); else printf("B 不去\n");
  17.                                 if(c==1) printf("C 去\n"); else printf("C 不去\n");
  18.                                 if(d==1) printf("D 去\n"); else printf("D 不去\n");
  19.                                 if(e==1) printf("E 去\n"); else printf("E 不去\n");
  20.                                 if(f==1) printf("F 去\n"); else printf("F 不去\n");     
  21.                             }
  22.                             e=1;
  23.                         }
  24.     return 0;
  25. }


6.数组重复元素问题
找出数组中重复的数字。在一个长度为 n （2 <= n <= 100000）的数组里的所有数字都在 1～n-1的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。
以输入 0 表示数组数字结束。请输出所有刚好重复了 2 次的数字，并按数字从小到大的顺序输出。
注意：重复的数字只输出一次。
示例：
输入：5 2 5 2 2 3 4 3 8 2 0
输出：3 5 

  1. #include <stdio.h>
  2. int main() {
  4. }

二：分治：归并排序、快速排序

0、课前热身题——程序调试
例题：阅读下面代码，说明程序的作用 

  1. #include <stdio.h>
  2. void r(){
  3.     char c;
  4.     scanf("%c", &c);
  5.     if( c != '\n')
  6.     {
  7.         r();
  8.         printf("%c",c);
  9.     }
  10. }
  11. int main(){
  12.     printf("输入一个字符串: ");
  13.     r();
  14.     return 0;
  15. }

1、复习冒泡排序
思路直观，代码最简单：算法重复地走访过要排序的数列，每次比较相邻的一对元素，如果他们的顺序错误（如从大到小、首字母从 Z 到 A），则交换它们的位置。

代码：依次比较相邻的两个数 a[j]和 a[j+1]，将小数放在前面，大数放在后面。 

  1. #include<stdio.h>
  2. #include<stdlib.h>
  3. void BubbleSort(int a[], int n){
  4.     int temp;
  5.     for (int i = 0; i < n-1; i++) {        // 外循环只要 n-1 次
  6.         for (int j = 0; j < n-1-i ; j++) { //内循环，把最大的数放在最后——沉底。
  7.                 //如果 a[j]比 a[j+1]大，则错位，交换
  8.                 if (a[j] > a[j + 1]) {
  9.                     temp = a[j];           //用中间变量交换数组两个位置的值
  10.                     a[j] = a[j + 1];
  11.                     a[j + 1] = temp;
  12.                 }
  13.          }
  14.     }
  15. }
  16. int main(){
  17.     int n = 10;
  18.     int a[] = {2,8,3,13,1,6,7,5,20,9 };
  19.     BubbleSort(a,n);
  20.     for (int q = 0; q < 10; q++)
  21.         printf("%d ", a[q]);
  22.     return 0;
  23. }

分治法概述

分治，字面上的解释是“分而治之”：把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。

分、治其实还有个合并的过程：
• 分(Divide)：递归解决较小的问题(到终止层或者可以解决的时候停下)
• 治(Conquer)：递归求解，如果问题够小直接求解。
• 合并(Combine)：将子问题的解构建父类问题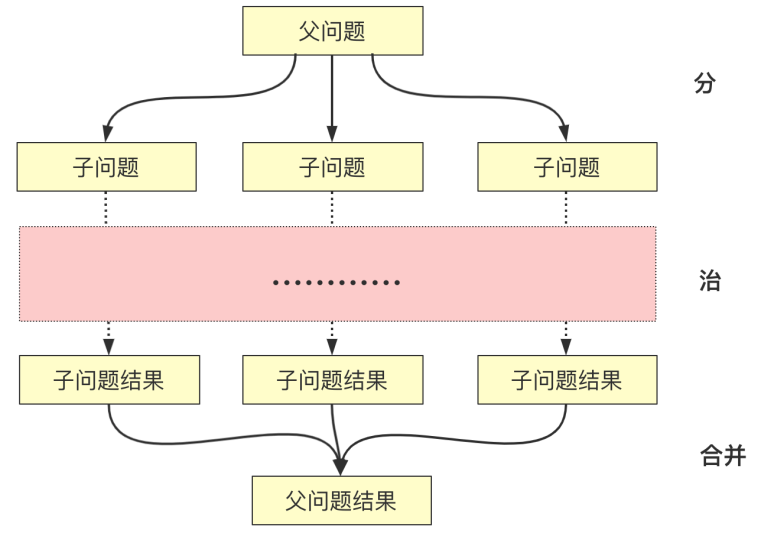
image.png


问题1：归并排序【分治思想，时间复杂度 O(nlogn)】

  1. #include <stdio.h>
  2. #include <stdlib.h>
  3. void MergeArray(int* a, int left, int mid, int right)
  4. {
  5.     int i = left;
  6.     int j = mid + 1;
  7.     int length = right - left + 1;int* temp = (int*)malloc((length) * sizeof(int));
  8.     int k = 0;
  9.     while (i <= mid && j <= right)
  10.     {
  11.         if (a[i] <= a[j])
  12.         {
  13.             temp[k] = a[i];
  14.             i++;
  15.             k++;
  16.         }
  17.         else
  18.         {
  19.             temp[k] = a[j];
  20.             j++;
  21.             k++;
  22.         }
  23.     }
  24.     while (i <= mid)
  25.     {
  26.         temp[k] = a[i];
  27.         i++;
  28.         k++;
  29.     }
  30.     while (j <= right)
  31.     {
  32.         temp[k] = a[j];
  33.         j++;
  34.         k++;
  35.     }//拷贝数据回原来数组
  36.     for (k = 0; k < length; k++)
  37.     {
  38.         a[left + k] = temp[k];
  39.     }
  40.     free(temp);
  41. }
  42. void MergeSort_Find(int* a, int left, int right){
  43.     if (left < right){
  44.         int mid = (left + right) / 2;
  45.         MergeSort_Find(a, left, mid);
  46.         MergeSort_Find(a, mid + 1, right);
  47.         MergeArray(a, left, mid, right);
  48.     }
  49. }
  50. int main(){
  51.     int i, a[100],n,key;
  52.     printf("请输入数组长度：\n");
  53.     scanf("%d",&n);
  54.     printf("请输入数组元素：\n");
  55.     for(i=0;i<n;i++)
  56.         scanf("%d",&a[i]);
  57.     MergeSort_Find(a,0,n-1);
  58.     printf("MAX=%d\nMIN=%d\n", a[n-1],a[0]);
  59.     return 0;
  60. }

3.2 快速排序【分治思想，时间复杂度 O(nlogn)】


4、实训题目

用分治法查找数组元素的最大值和最小值
要求：使用分治的算法，根据不同的输入用例，能准确的输出用例中的最
大值与最小值。
程序思路：利用分治法，将一个数组元素个数大于 2 的数组分成两个子数
组，然后对每一个子数组递归调用，直到最小的子数组的元素个数为 1 个或者
是 2 个，此时直接就能得出最大值与最小值，然后合并子数组，比较 2 个子数
组的最大值与最小值，依次进行下去，知道找到整个数组的最大值与最小值。
/*以下为测试数据
test1：
8
1 4 15 -3 6 12 -5 9
result1：
MAX = 15
MIN = -5
——————————————-
test2：
7
1 4 15 -3 6 12 -5
result2：
MAX = 15
MIN = -5
——————————————-
test3：
2
1 4
result3：
MAX = 4
MIN = 1
——————————————-
test4：
1 -
50
result4：
MAX = -50
MIN = -50 

  1. #include <stdio.h>
  2. #include <stdlib.h>
  3. void MergeArray(int* a, int left, int mid, int right)
  4. {
  5.     int i = left;
  6.     int j = mid + 1;
  7.     int length = right - left + 1;int* temp = (int*)malloc((length) * sizeof(int));
  8.     int k = 0;
  9.     while (i <= mid && j <= right)
  10.     {
  11.         if (a[i] <= a[j])
  12.         {
  13.             temp[k] = a[i];
  14.             i++;
  15.             k++;
  16.         }
  17.         else
  18.         {
  19.             temp[k] = a[j];
  20.             j++;
  21.             k++;
  22.         }
  23.     }
  24.     while (i <= mid)
  25.     {
  26.         temp[k] = a[i];
  27.         i++;
  28.         k++;
  29.     }
  30.     while (j <= right)
  31.     {
  32.         temp[k] = a[j];
  33.         j++;
  34.         k++;
  35.     }//拷贝数据回原来数组
  36.     for (k = 0; k < length; k++)
  37.     {
  38.         a[left + k] = temp[k];
  39.     }
  40.     free(temp);
  41. }
  42. void MergeSort(int* a, int left, int right){
  43.     if (left < right){
  44.         int mid = (left + right) / 2;
  45.         MergeSort(a, left, mid);
  46.         MergeSort(a, mid + 1, right);
  47.         MergeArray(a, left, mid, right);
  48.     }
  49. }
  50. int main(){
  51.     int a[10] = { 5, 2, 11, 6, 7, 3 , 9 ,10 ,1 ,4};
  52.     int n = 10;
  53.     MergeSort(a, 0, 9);
  54.     printf("MAX=%d\nMIN=%d\n", a[10-1],a[0]);
  55.     return 0;
  56. }


二：分治加强：最优股票利润

问题1：股票最大买入卖出方案——最大连续子段和问题

问题：给定一个 int 数组，长度为 n，数组中存放的是某只股票 n 天来的相对于前一交易日的股价涨跌情况。求在一次买入、卖出的操作下，能获得的最大利润。

例如[3, -7, 4, -3, 5, -2, -1, 2, 6, -2]，它的最大利润为 11=[4+(-3)+5+(-2)+(-1)+(2)+(6)]。
此问题实质上是求该序列连续的子段和的最大值，即最大连续子序列之和。
又比如，对一个数列[-2, 1, -3, 4, -1, 2, 1, -5, 4]，其连续子数列中和最大的是[4, -1, 2, 1]，其和为6。
解决该问题有很多方法可以通过暴力、分治和动态规划法。


a：暴力法

• 思想：从序列首元素开始穷举所有可能的子序列。
• 算法复杂度为 O(n3)。 改进的蛮力算法，直接在划定子序列时累加元素值，减少一层循环。

  1. #include <stdio.h>
  2. #include <string.h>
  3. #include <stdlib.h>
  4. int main(int argc, char** argv)
  5. {
  6.     int n = 10;
  7.     int a[] = { 3, -7, 4, -3, 5, -2, -1, 2, 6, -2 };
  8.     int maxSum = INT_MIN;
  9.     int indexI, indexJ;
  10.     for (int i = 0; i < n; i++)
  11.     {
  12.         for (int j = n - 1; j >= i; j--)
  13.         {
  14.             int tempSum = 0;
  15.             for (int k = i; k <= j; k++)
  16.                 tempSum += a[k];
  17.             if (tempSum > maxSum)
  18.             {
  19.                 maxSum = tempSum;
  20.                 indexI = i;
  21.                 indexJ = j;
  22.             }
  23.         }
  24.     };
  25.     printf("Max sum array is from a[%d]...a[%d], and the sum is : %d",indexI, indexJ, maxSum);
  26.     return 0;
  27. }

b：分治法

• 思想：将序列划分为左右两部分，则最大子段和可能在三处出现：左半部、右半部以及跨越左右边界的部分。递归的终止条件是： left == right。
过程：
在数组的 mid = (left+right)/2 位置处分开，形成两个子数组。那么，最大子段和 可能出现在三个位置：
1.可能出现在 左子数组
2.可能出现在 右子数组
3.可能出现在 过 mid 的 中间某部分 元素 组成的子数组。

b.1 版：求跨边界最大子段 left_right_Max 还是用穷举法。

image.png

  1. #include <stdio.h>
  2. #include <string.h>
  3. #include <stdlib.h>
  4. int max3(int a, int b, int c)
  5. {
  6.     int max = a;
  7.     if (b > max)
  8.             max = b;
  9.     if (c > max)
  10.             max = c;
  11. }
  12. void findMaxSum(int a[], int left, int right, int* maxSum)
  13. {
  14.     if (left < right) // 设置递归条件，即大问题分解为小问题的条件。如果不满足，则递归终止
  15.     {
  16.         int mid = (left + right) / 2;
  17.         int left_Max, right_Max, left_right_Max = 0;
  18.         findMaxSum(a, left, mid, &left_Max); // 递归求左半部分最大子序列和
  19.         findMaxSum(a, mid + 1, right, &right_Max); // 递归求右半部分最大子序列和
  20.         // 处理左右边界问题：最大子序列跨越中间，包含左半部分最右一个数，同时包含右半部分最左一个数
  21.         for (int i = left; i <= mid; i++)
  22.         {
  23.             for (int j = right; j >= mid + 1; j--)
  24.             {
  25.                 int sum = 0; // 临时求和变量
  26.                 for (int k = i; k <= j; k++)
  27.                 sum += a[k];
  28.                 if (sum > left_right_Max)
  29.                     left_right_Max = sum;
  30.             }
  31.         }
  32.         *maxSum = max3(left_Max, right_Max, left_right_Max); // 返回三个部分的最大子序列和
  33.     } 
  34.     else
  35.             *maxSum = a[left];
  36.     }
  37. int main(int argc, char** argv){
  38.         int n = 10;
  39.         int a[] = { 3, -7, 4, -3, 5, -2, -1, 2, 6, -2 };
  40.         int maxSum = INT_MIN;
  41.         findMaxSum(a, 0, n - 1, &maxSum);
  42.         printf("最大字段和为: %d", maxSum);
  43.         return 0;
  44. }

b.2 版：求跨边界的最大子段 left_right_Max 用分治法。

b.1算法时间复杂度非常高,需优化。
改进 left_right_Max 的求法：以 mid 为中心分别向两边计算和。
a.从 mid 出发，每次向左边扩张一步，并且记录当前的和值 sum，如果当前的和比 S1 大，就更新 S1，一直向左扩张到位置 Left。
b.从 mid +1 出发，每次扩张一步，计算当前的和 sum，如果当前的值比 S2 大，那么，就更新 S2 的值，一直向右扩张到位置 Right。
c.计算过 mid 的连续值的和， S1+S2 的值 Sum。 这个就是跨边界的和
image.png

  1. #include <stdio.h>
  2. #include <string.h>
  3. #include <stdlib.h>
  4. int max3(int a, int b, int c)
  5.     {
  6.     int max = a;
  7.     if (b > max)
  8.            max = b;
  9.     if (c > max)
  10.             max = c;
  11.     }
  12. void findMaxSum(int a[], int left, int right, int* maxSum){
  13.     if (left < right) // 设置递归条件，即大问题分解为小问题的条件。如果不满足，则递归终止
  14.     {
  15.         int mid = (left + right) / 2;
  16.         int left_Max, right_Max, left_right_Max;
  17.         findMaxSum(a, left, mid, &left_Max); // 求左半部分最大子序列和
  18.         findMaxSum(a, mid + 1, right, &right_Max); // 求右半部分最大子序列和
  19.         // 处理左右边界问题：最大子序列跨越中间，包含左半部分最右一个数，同时包含右半部分最左一个数
  20.         int S1 = 0, S2 = 0;
  21.         int sum = 0; // 临时求和变量
  22.         for (int i = mid; i >= left; i--)
  23.         {
  24.             sum += a[i];
  25.             if (sum > S1)
  26.                  S1 = sum; // 左边包含边界最大序列和
  27.         }
  28.         sum = 0;
  29.         for (int j = mid + 1; j <= right; j++)
  30.         {
  31.             sum += a[j];
  32.             if (sum > S2)
  33.                  S2 = sum; // 右边包含边界最大序列和
  34.         }
  35.         left_right_Max = S1 + S2; // 最大边界子序列和等于两部分边界之和
  36.         *maxSum = max3(left_Max, right_Max, left_right_Max); // 返回三个部分的最大子序列和
  37.     }
  38.     else
  39.             *maxSum = a[left];
  40. }
  41. int main(int argc, char** argv)
  42. {
  43.     int n = 10;
  44.     int a[] = { 3, -7, 4, -3, 5, -2, -1, 2, 6, -2 };
  45.     int maxSum = INT_MIN;
  46.     findMaxSum(a, 0, n - 1, &maxSum);
  47.     printf("最大字段和为: %d", maxSum);
  48.     return 0;
  49. }

c.动态规划法

用数组 dp[j]表示序列 a[1,…,j]中以 a[j]结尾的（注意，必须含有元素 a[j]），向前连续延伸的最
大子段的和的值，
若数组 dp 的全部元素可以求出来，则原问题则所求的最大子段和为
由 b[j]的定义可易知：
当 b[j-1]>0 时， b[j]=b[j-1]+a[j]
否则 b[j]=a[j]。
故 b[j]的动态规划递归式为:
T(n)=O(n)
//时间复杂度为 O(n) 

  1. #include <stdio.h>#include <string.h>
  2. #include <stdlib.h>
  3. int main(int argc, char** argv)
  4. {
  5. int n = 10;
  6. int a[] = { 3, -7, 4, -3, 5, -2, -1, 2, 6, -2 };
  7. int dp[10];
  8. dp[0] = a[0];
  9. //计算动态数组
  10. for (int i = 1; i < n; i++)
  11. {
  12. dp[i] = max(dp[i - 1] + a[i], a[i]);
  13. }
  14. //找出数组最大子段和
  15. int maxSum = INT_MIN;
  16. for (int j = 0; j < n; j++)
  17. {
  18. maxSum = max(maxSum, dp[j]);
  19. }
  20. printf("最大字段和为: %d", maxSum);
  21. return 0;
  22. }

5、作业
作业 1、二分查找
二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。
算法要求：
1.必须采用顺序存储结构。
2.必须按关键字大小有序排列。
查找过程
首先，假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；
否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。
重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功（返回-1）。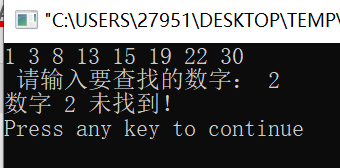
image.png

  1. int BinarySearch(int* a, int len, int key)
  2. {
  3.     int l=0, r=n-1,mid=0;
  4.     while (l<=r)
  5.     {
  6.         int mid= l+(r-l)/2;    //避免溢出
  7.         if(a[mid]==key)
  8.            return mid ;        //返回要查找元素的下标
  9.         if(key>a[mid])
  10.            l=mid+1;
  11.         else 
  12.            r=mid-1;
  13.     }
  14.     return 0;
  15. }
  16. int main() {
  17.     int a[8] = {1,3,8,13,15,19,22,30};
  18.     for (int q = 0; q < 8; q++)
  19.         printf("%d ", a[q]);
  20.     printf("\n 请输入要查找的数字： ");
  21.     int key;
  22.     scanf("%d",&key);
  23.     int index = BinarySearch(a,8,key);
  24.     if (index>=0)
  25.            printf("数字 %d 的下标为 %d\n",key,index);
  26.     else
  27.            printf("数字 %d 未找到！ \n",key);return 0;
  28. }

三：动态规划：走楼梯、数塔

问题1：爬楼梯问题

有一座高度是 10 级台阶的楼梯，从下往上走， 每跨一步只能向上 1 级或者 2 级台阶。要求用程序来求出一共有多少种走法。
比如，每次走 1 级台阶，一共走 10 步，这是其中一种走法。我们可以简写成1,1,1,1,1,1,1,1,1,1。
再比如，每次走 2 级台阶，一共走 5 步，这是另一种走法。我们可以简写成2,2,2,2,2。
当然，除此之外，还有很多很多种走法。


a.暴力法

用排列组合的思想，写一个多层嵌套循环遍历所有的可能性。每遍历出一个组合，让计数器加一。
缺点：算法时间复杂度将是指数级。


b.动态规划法

假设你只差最后一步走到第十级楼梯，这时会出现几种情况呢？
由于每一步只能走 1 级或者 2 级，所以只有两种情况。
第一种情况是从第 9 级走到第 10 级。
第二种情况是从第 8 级走到第 10 级。
咱们暂且不管从 0 走到 8 级台阶的过程，也不管从 0 级走到 9 级台阶的过程。
想要走到第 10 级，最后一步必然是从 8 级或者 9 级开始。
接下来引申出一个新的问题：如果我们已知 0 到 9 级台阶的走法有 X 种， 0 到 8级台阶的走法有 Y 种，那么 0 到 10 级台阶的走法有多少种?
答案是 X+Y 种。
10 级台阶的所有走法可以根据最后一步的不同而分成两部分。
第一部分的最后一步是从 9 级到 10 级，这部分的走法数量和 9 级台阶的走法数量是相等的，也就是 X。
第二部分的最后一步是从 8 级到 10 级，这部分的走法数量和 8 级台阶的走法数量是相等的，也就是 Y。
这两部分相加，总的走法数量是 X+Y!
这样一来就可以得出一个结论：
从 0 到 10 级台阶的走法数量 = 0 到 9 级的走法数量 + 0 到 8 级的走法数量。
可以简单表示为 F(10) = F(9) + F(8)
那么，我们如何计算 F(9)和 F(8)呢?
利用刚才同样的思路，不难得到：
F(9) = F(8) + F(7)
F(8) = F(7) + F(6)
…………
我们正在把一个复杂的问题分阶段进行简化，逐步简化成简单的问题。这就是
动态规划的思想。
F(1) = 1
F(2) = 2
F(n) = F(n-1) + F(n-2) 当 n≥3
动态规划当中包含三个重要的概念:【最优子结构】、【边界】、【状态转移公
式】。
• 刚才我们分析出 F(10)= F(9)+F (8),因此 F(9)和 F(8)是 F(10)的【最优子结
构】。
• 当只有 1 级台阶或 2 级台阶时,我们可以直接得出结果，无需继续简化。我们称
F(1)和 F(2)是问题的【边界】。如果一个问题没有边界，将永远无法得到有限
的结果。

【状态转移方程】

• F(n)= F(n-1)+F(n-2)是阶段与阶段之间的【状态转移方程】。这是动态规划的核心，决定了问题的每一个阶段和下一阶段的关系。

b.1 简单递归实现

  1. #define _CRT_SECURE_NO_WARNINGS
  2. #include <stdio.h>
  3. #include <string.h>
  4. #include <stdlib.h>
  5. int getClimbingWays(int n, int * count)
  6. {
  7.     (*count)++;
  8.     if (n <  1)     return 0;
  9.     if (n == 1)     return 1;
  10.     if (n == 2)     return 2;
  11.     return getClimbingWays(n-1,count) + getClimbingWays(n-2,count);
  12. }
  13. int main(int argc, char** argv)
  14. {
  15.     int n,count=0;
  16.     printf("请输入 n=");
  17.     scanf("%d", &n);
  18.     printf("走法有%d 种\n", getClimbingWays(n,&count));
  19.     printf("递归调用了%d 次", count);
  20.     return 0;
  21. }

b.2 递归实现的优化——备忘录法（自顶向下求解）

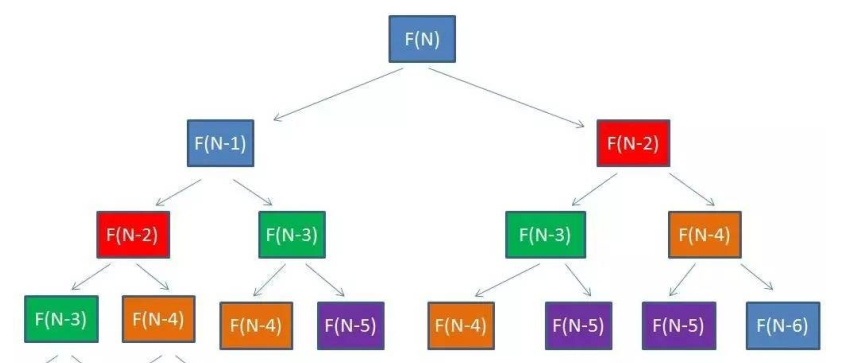
很多子问题被重复计算了。下图中， 相同的颜色代表了方法被传入相同的参数。 image.png
对于这种存在大量子问题重复计算的情况，如何避免？
可以把计算结果暂存起来——就是所谓的【备忘录算法】。 

  1. #define _CRT_SECURE_NO_WARNINGS
  2. #include <stdio.h>
  3. #include <string.h>
  4. #include <stdlib.h>
  5. int result[1000];
  6. int getClimbingWays(int n)
  7. {
  8.     if (n <  1)        return 0;
  9.     if (n == 1)        return 1;
  10.     if (n == 2)     return 2;
  11.     if (result[n] != -1)    return result[n];
  12.     else {
  13.         result[n] = getClimbingWays(n - 1) + getClimbingWays(n - 2);
  14.         return result[n];
  15.     }
  16. }
  17. int main(int argc, char** argv)
  18. {
  19.     int n;
  20.     printf("请输入 n=");
  21.     scanf("%d", &n);
  22.     for (int i = 0; i <= n; i++)
  23.     {
  24.            result[i] = -1;
  25.     }
  26.     printf("走法有%d 种\n", getClimbingWays(n));
  27.     return 0;
  28. }

b.3 自底向上法求解

我们回到一开始的思路，我们是假定前面的楼梯已经走完，只考虑最后一步，所以才得出来 f(n) = f(n-1) + f(n-2)的递归式，这是一个自顶向下求解的式子
一般来说，按照正常的思路应该是一步一步往上走，应该是自底向上去求解才比较符合正常人的思维。
这是一开始走的一个和两个楼梯的走法数,即之前说的初始状态
这是进行了一次迭代得出了 3 个楼梯的走法， f(3)只依赖于 f(1) 和f(2)。继续看下一步
这里又进行了一次迭代得出了 4 个楼梯的走法， f(4)只依赖于 f(2) 和f(3)
我们发现每次迭代只需要前两次迭代的数据，不用像备忘录一样去保存所有子状态的数据
这时我们可以再看看当前的时间复杂度和空间复杂度当前时间复杂度仍为 O(n)，但空间复杂度降为 O(1)这就是理想的结果 

  1. #define _CRT_SECURE_NO_WARNINGS
  2. #include <stdio.h>
  3. #include <string.h>
  4. #include <stdlib.h>
  5. int result[1000];
  6. int getWays(int n)
  7. {
  8.     //方法 1
  9.     //if (n < 1)
  10.     // return 0;
  11.     //if (n == 1)
  12.     // return 1;
  13.     //if (n == 2)
  14.     // return 2;
  15.     //
  16.     //int a = 1, b = 2;
  17.     //int temp = a + b;
  18.     //for (int i = 3; i <= n; i++)
  19.     //{
  20.     // temp = a + b;
  21.     // a = b;
  22.     // b = temp;
  23.     //}
  24.     //return temp;//方法 2
  25.     result[1] = 1;
  26.     result[2] = 2;
  27.     for (int i = 3; i <= n; i++)
  28.     {
  29.         result[i] = result[i-1] + result[i-2];
  30.     }
  31.         return result[n];
  32. }
  33. int main(int argc, char** argv)
  34. {
  35.     int n;
  36.     printf("请输入 n=");
  37.     scanf("%d", &n);
  38.     printf("走法有%d 种\n", getWays(n));
  39.     return 0;
  40. }

问题2：数塔问题

数字塔是第 i 行有 i 个数字组成， 从上往下每个数字只能走到他正下方数字或
者正右下方数字，求数字塔从上到下所有路径中和最大的路径的全体数字之
和。
如有下数字塔
3
1 5
8 4 3
2 6 7 9
6 2 3 5 1
最大路径是 3-5-3-9-5，和为 25。
从下往上看时：
每进来上面一行，上面一行每个数字有两条路径到达下面一行，所以选一条最大的就可以
所以最大值就是最上面数字就是 25.
具体方法也是建立一个二维数组，最下面一行数据添到二维数组最后一行，从
下往上填数字，所以状态转化方程是 dp[i][j]=Math.max(dp[i+1][j+1],dp[i+1][j]) + n[i][j]
数塔中元素用二维数组 a[][]表示
可设 dp[i][j]为第 i 层的第 j 个顶点到底层经过的最大数字和。
所以我们可以从后往前推出状态转移方程（逆向思维），
dp[0][0]等于第 1 层第 1 个数字到底层经过的最大数字和，它等于 dp[1][0] +
a[0][0]或 dp[1][1] + a[0][0]中的最大的数值。

【状态转移方程】

我们可以公式化，得到如下状态转换方程：
dp[i][j] = max( dp[i+1][j] + dp[i+1][j+1] ) + a[i][j]
由状态定义我们可以得出当数字在最底层时，它到最底层就是数字本身，即可
得出 dp[i][j] = a[i][j] (0≤i,j≤N)
作业要求：写出 dp 数组的手工计算结果

25
18 22
17 16 17
8 9 12 14
6 2 3 5 1

三：动态规划加强

动态规划基本框架

⾸先，动态规划问题的⼀般形式就是求最值：⽐如最⼤连续⼦段和、爬楼梯问题求的有多少种爬楼⽅法、数塔问题的最⼤数字和。
既然是要求最值，核⼼问题是什么呢？求解动态规划的核⼼问题是穷举。因为要求最值，肯定要把所有可⾏的答案穷举出来，然后在其中找最值呗。
但是，为了优化算法的效率，⼜不⽤直接穷举的⽅法。
⾸先，动态规划的穷举有点特别，因为这类问题存在「重叠⼦问题」，如果暴⼒穷举的话效率会极其低下，所以需要「备忘录」或者「DP 数组」来优化穷举过程，避免不必要的计算。
⽽且，动态规划问题⼀定会具备「最优⼦结构」，才能通过⼦问题的最值得到原问题的最值。
另外，虽然动态规划的核⼼思想就是穷举求最值，但是问题可以千变万化，穷举所有可⾏解其实并不是⼀件容易的事，只有列出正确的「状态转移⽅程」才能正确地穷举。

以上提到的重叠⼦问题、最优⼦结构、状态转移⽅程就是动态规划三要素。
重叠⼦问题：是⼀个递归解决⽅案⾥包含的⼦问题虽然很多，但不同⼦问题很少。少量的⼦问题被重复解决很多次。
例⼦：爬楼梯问题就可以分解为许多⼦问题，⽽且这些⼦问题是重叠的，要重复计算多次。⽽归并排序也有很多⼦问题，但是这些⼦问题是相互独⽴的，不重叠的。
最优⼦结构性质（最优化原理）是指原问题的最优解包含⼦问题的最优解。
例如：⼀个国家中跑步最快的运动员(问题的最优解)，那么他必须是他所在省份中跑步最快的运动
员(⼦问题的最优解)，这样他才可能是这个国家最快的运动员。
例如：数塔问题和爬楼梯问题。
在实际的算法问题中，写出状态转移⽅程是最困难的。
下⾯给出⼀个思维框架，辅助你思考状态转移⽅程：
明确 base case -> 明确「状态」-> 明确「选择」 -> 定义 dp 数组/函数的含义。
按上⾯的套路⾛，最后的结果就可以套这个框架：

  1. // 初始化 base case
  2. dp[0][0][...] = base
  3. // 进⾏状态转移
  4. for 状态1 in 状态1的所有取值：
  5.     for 状态2 in 状态2的所有取值：
  6.         for ...
  7.                 dp[状态1][状态2][...] = 求最值(选择1，选择2...)

问题1：零钱问题

假设您是个⼟豪，身上带了⾜够数量的1、5、10、20、50、100元⾯值的钞票。现在您的⽬标是凑出某个⾦额w，需要⽤到尽量少的钞票数量。

a.贪心法局限

依据⽣活经验，先凑大的再小的。这种策略称为“贪⼼”：假设我们⾯对的局⾯是“需要凑出w”，贪⼼策略会尽快让w变得更⼩。能让w少100就尽量让它少100，这样我们接下来⾯对的局⾯就是凑出w-100。⻓期的⽣活经验表明，贪⼼策略是正确的。
但是，如果我们换⼀组钞票的⾯值，贪⼼策略就也许不成⽴了。如果⼀个奇葩国家的钞票⾯额分别是1、5、11，那么我们在凑出15的时候，贪⼼策略会出错：
15=1×11+4×1 （贪⼼策略使⽤了5张钞票）
15=3×5 （正确的策略，只⽤3张钞票）
为什么会这样呢？贪⼼策略错在了哪⾥？
⿏⽬⼨光。
刚刚已经说过，贪⼼策略的纲领是：“尽量使接下来⾯对的w更⼩”。这样，贪⼼策略在w=15的局⾯时，会优先使⽤11来把w降到4；但是在这个问题中，凑出4的代价是很⾼的，必须使⽤4×1。如果使⽤了5，w会降为10，虽然没有4那么⼩，但是凑出10只需要两张5元。
在这⾥我们发现，贪⼼是⼀种只考虑眼前情况的策略。
那么，现在我们怎样才能避免⿏⽬⼨光呢？

b.动态规划法

如果直接暴⼒枚举凑出amount的⽅案，明显复杂度过⾼。太多种⽅法可以凑出amount了，枚举它们的时间是不可承受的。我们现在来尝试找⼀下性质。
重新分析刚刚的例⼦。amount=15时，我们如果取11，接下来就⾯对amount=4的情况；如果取5，则接下来⾯对amount=10的情况。
我们发现这些问题都有相同的形式：“给定amount，凑出amount所⽤的最少钞票是多少张？”接下来，我们⽤ 来表示“凑出n所需的最少钞票数量”。
那么，amount=15时，我们如果先取11，最后的代价（⽤掉的钞票总数）是多少呢？
明显，代价 ，它的意义是：利⽤11来凑出15，付出的代价等于
f(4)加上⾃⼰这⼀张钞票。现在我们暂时不管f(4)怎么求出来。
依次类推，⻢上可以知道：

amount=15时，我们如果先取5，最后的代价
amount=15时，我们如果先取1，最后的代价		 。
。

那么，现在amount=15的时候，我们该取那种钞票呢？当然是各种⽅案中，cost值最低的那⼀个！
- 取11：
- 取5：
- 取1：
显⽽易⻅，cost值最低的是取5的⽅案。我们通过上⾯三个式⼦，做出了正确的决策！
4
这给了我们⼀个⾄关重要的启示：
只与 相关；
更确切地说：

【状态转移方程】

这个式⼦是⾮常激动⼈⼼的。我们要求出 ，只需要求出⼏个更⼩的
们从⼩到⼤把所有的 求出来不就好了？注意⼀下边界情况即可。

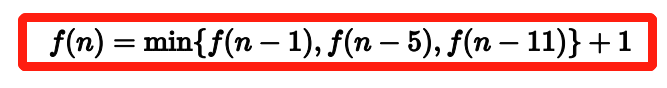
image.png
值；既然如此，我
回顾⼀下本题的算法设计过程：
1、确定 base case，这个很简单，显然⽬标⾦额 amount 为 0 时算法返回 0，因为不需要任何硬币
就已经凑出⽬标⾦额了。
2、确定「状态」，也就是原问题和⼦问题中会变化的变量。由于钞票数量⽆限，钞票的⾯额也是题⽬
给定的，只有⽬标⾦额会不断地向 base case 靠近，所以唯⼀的「状态」就是⽬标⾦额 amount 。
3、确定「选择」，也就是导致「状态」产⽣变化的⾏为。⽬标⾦额为什么变化呢，因为你在选择硬
币，你每选择⼀枚硬币，就相当于减少了⽬标⾦额。所以说所有硬币的⾯值，就是你的「选择」。
4、明确 dp 函数/数组的定义。⾃顶向下的解法会有⼀个递归的 dp 函数，⾃底向上使⽤ dp 数组来
辅助。 dp 函数体现在函数参数，⽽ dp 数组体现在数组索引： dp 数组的定义：当⽬标⾦额为 i
时，⾄少需要 dp[i] 枚硬币凑出。
⾃


b.1.顶向下法（带备忘录的递归）

略

b.2.⾃底向上法（dp数组）

代码如下 

  1. #define _CRT_SECURE_NO_WARNINGS
  2. #include <stdio.h>
  3. #include <string.h>
  4. #include <stdlib.h>
  5. int min3(int a, int b, int c)
  6. {
  7.     int min = a;
  8.     if (b < min) min = b;
  9.     if (c < min) min = c;
  10.     return min;
  11. } 
  12. void coinChange(int amount, int coins[]) //⾃底向上求解dp数组
  13. {
  14.     int dp[1001];
  15.     dp[0] = 0;
  16.     for (int i = 1; i <= amount; i++) //外循环，遍历所有的状态
  17.     {
  18.         int cost = INT_MAX; // 成本——i⾦额所需要的最少的硬币数量。
  19.         //for (int j = 0; j < 3; j++) //内循环，遍历所有的“选择 / 币值”
  20.         //{
  21.         // int coin = coins[j];
  22.         // if (coin > i) continue; // 此⾯值的硬币不适⽤，则跳过
  23.         // cost = min(cost,dp[i - coin] + 1); // 计算此选择（币值）下的成本，如果⽐已经找到的最⼩成本更⼩，则更新cost
  24.         //}
  25.         int cost1 = INT_MAX;  // 选择币值为1的“成本”
  26.         int cost5 = INT_MAX;  // 选择币值为5的“成本”
  27.         int cost11 = INT_MAX; // 选择币值为11的“成本”
  28.         if (1 <= i)
  29.         cost1 = dp[i - 1] + 1;
  30.         if (5 <= i)
  31.         cost5 = dp[i - 5] + 1;
  32.         if (11 <= i)
  33.         cost11 = dp[i - 11] + 1;
  34.         cost = min3(cost1, cost5, cost11);
  35.         dp[i] = cost;
  36.         printf("dp[%d]=%d\n",i, dp[i]);
  37.     }
  38. }
  39. int main(int argc, char** argv)
  40. {
  41.     int coins[] = { 1,5,11 };
  42.     int amount;
  43.     printf("请输⼊⾦额=");
  44.     scanf("%d", &amount);
  45.     coinChange(amount,coins);
  46.     return 0;
  47. }

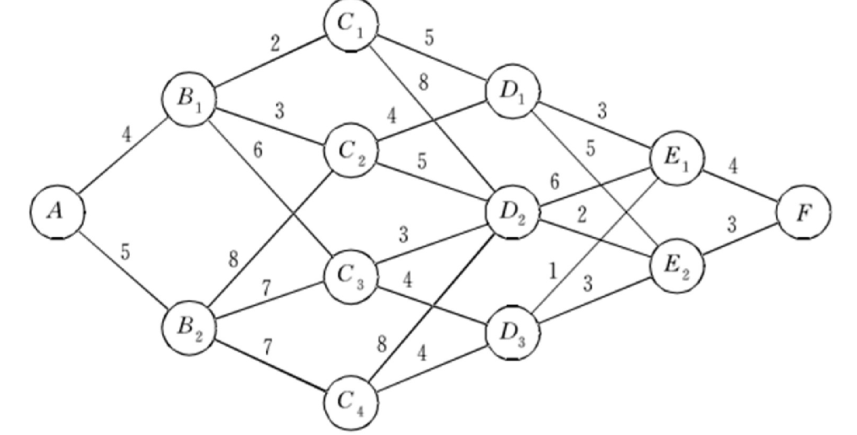
问题2：最短路径

问题很简单：不回退的前提下，找到A到F的最短路径。
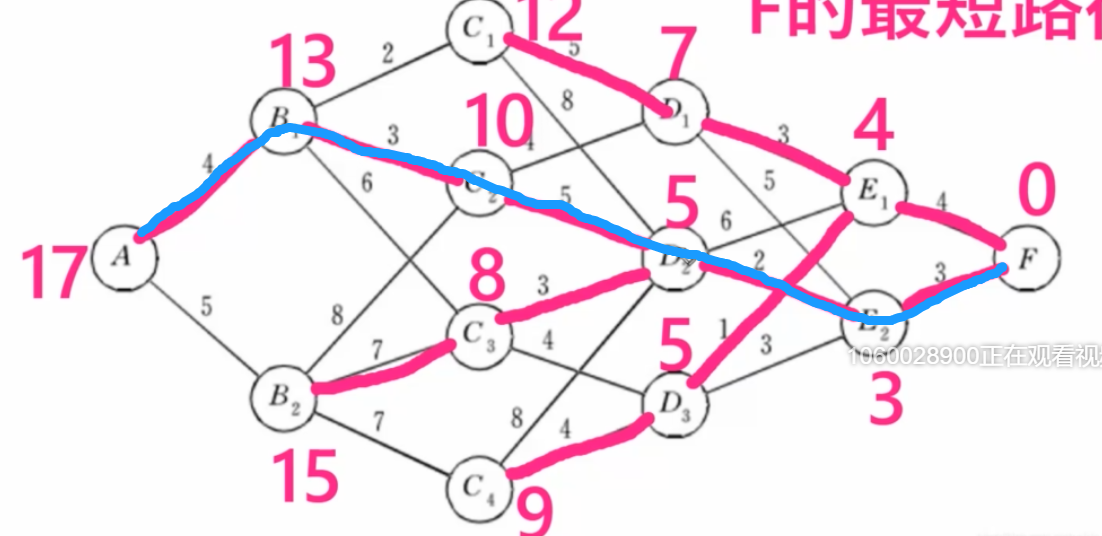
image.pngimage.png

问题3：最⼤连续⼦段和问题

dp数组从下标1开始
作业：要求要有过程，要画出表格。
1、计算题：零钱问题。我们有⾯值为1元3元5元的硬币若⼲枚，凑够11元最少需要多少枚硬币？求出其dp数组。


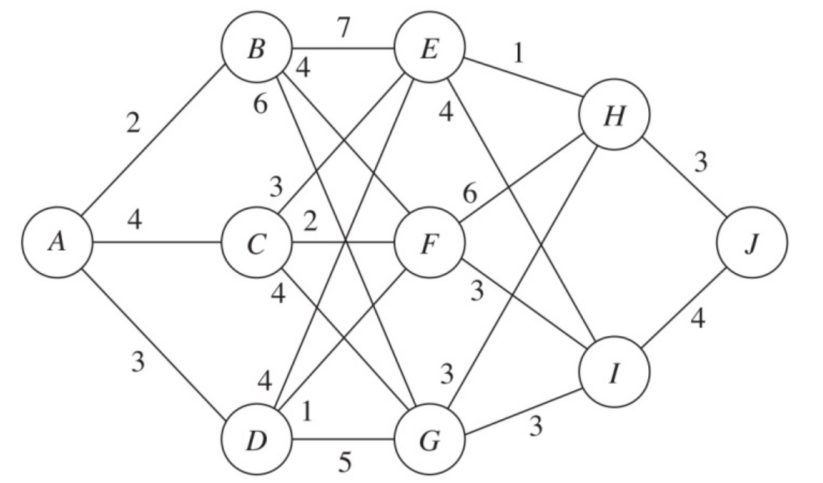
2、计算题：最短路径问题。求出下图的A到J的最短路径⻓度。并说明最短路径的顶点序列。
image.png
3、计算题：最⼤⼦序列和问题。对于数组 [3, -2, 1, -4, 5, -5 , 6, -3, 7, -5, 4 ]。求出其dp数组，并说明最⼤和是多少。

4、编程题：爬楼梯问题。楼梯有 15 阶台阶，我们⼀步可以踏上可以上 1 阶、2 阶或 3 阶。编写程序，输出有多少种上楼梯的⽅式。

四：贪心

问题1：零钱问题

  1. #define _CRT_SECURE_NO_WARNINGS
  2. #include<stdio.h>
  3. #include<string.h>
  4. #include<stdlib.h>
  5. int main()
  6. {
  7.     int w;
  8.     int amount[6];
  9.     int coins[6] = { 1, 5, 10, 20, 50, 100};
  11.     printf("输入金额=");
  12.     scanf("%d",&w);
  14.     for (int i=5;i>=0;i--){
  15.         amount[i] = w/coins[i];
  16.         w = w % coins[i];
  17.         printf("面值为%d的硬币%d枚\n",coins[i],amount[i]);
  18.     }
  19.     return 0;
  20. }

问题2：背包问题

四：贪心加强