883. 三维形体投影面积

1. 题目描述

https://leetcode-cn.com/problems/projection-area-of-3d-shapes/
在 的网格 grid 中，我们放置了一些与 x，y，z 三轴对齐的 立方体。
每个值 表示 个正方体叠放在单元格 #card=math&code=%28i%2C%20j%29&id=yU7Qa) 上。
现在，我们查看这些立方体在 xy、yz 和 zx 平面上的投影。
投影 就像影子，将 三维 形体映射到一个 二维 平面上。从顶部、前面和侧面看立方体时，我们会看到“影子”。
返回 所有三个投影的总面积 。

示例 1：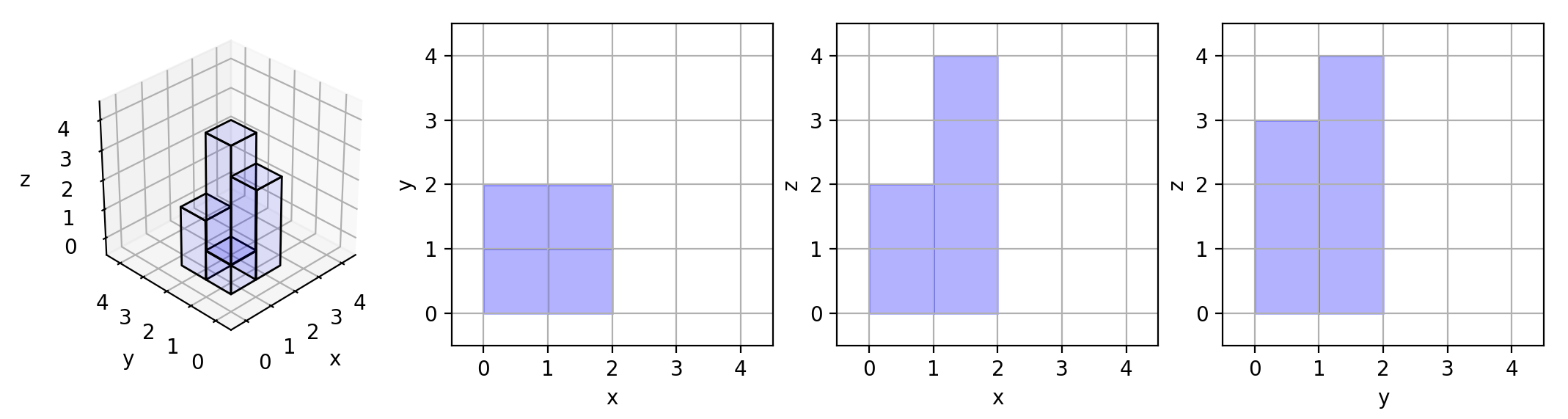

输入：[[1,2],[3,4]]
输出：17
解释：这里有该形体在三个轴对齐平面上的三个投影(“阴影部分”)。
示例 2:
输入：grid = [[2]]
输出：5
示例 3：
输入：[[1,0],[0,2]]
输出：8
提示：

2. 题解

2022-04-26 AC, 题是简单题, 需要点几何想象力, 求出x y z的规律即可
ans1：统计俯视图的面积，共有 $n n$ 个位置需要被统计，当任意格子 $g[i][j] > 0$，阴影面积加一；
*ans2：统计左视图的面积，共有 $n$ 行需要被统计，每一行对 ans2 的贡献为该行的最大高度；
*ans3：统计主视图的面积，共有 $n$ 列需要被统计，每一列对 ans3 的贡献为该列的最大高度。

<?php
/**
 * Created by PhpStorm
 * User: jtahstu
 * Time: 2022/4/26 22:24
 * Des: 883. 三维形体投影面积
 *      https://leetcode-cn.com/problems/projection-area-of-3d-shapes/
 *      在 n x n 的网格 grid 中，我们放置了一些与 x，y，z 三轴对齐的 1 x 1 x 1 立方体。
 * 每个值 v = grid[i][j] 表示 v 个正方体叠放在单元格 (i, j) 上。
 * 现在，我们查看这些立方体在 xy 、yz 和 zx 平面上的投影。
 * 投影 就像影子，将 三维 形体映射到一个 二维 平面上。从顶部、前面和侧面看立方体时，我们会看到“影子”。
 * 返回 所有三个投影的总面积 。
 */
class Solution
{
    /**
     * @param Integer[][] $grid
     * @return Integer
     */
    function projectionArea($grid)
    {
        $x = $y = $z = 0;
        $index_max = [];
        foreach ($grid as $row) {
            $max = -1;
            foreach ($row as $k => $count) {
                $z += $count > 0 ? 1 : 0;
                $max = max($max, $count);
                $index_max[$k][] = $count;
            }
            $x += $max;
        }
        foreach ($index_max as $y_max) {
            $y += max($y_max);
        }
//        print_r([$x, $y, $z]);
        return $x + $y + $z;
    }
}
var_dump((new Solution())->projectionArea([[1, 2], [3, 4]]));
var_dump((new Solution())->projectionArea([[2]]));
var_dump((new Solution())->projectionArea([[1, 0], [0, 2]]));
/**
 * 执行用时：24 ms, 在所有 PHP 提交中击败了50.00%的用户
 * 内存消耗：19 MB, 在所有 PHP 提交中击败了100.00%的用户
 * 通过测试用例：90 / 90
 */