427. 建立四叉树

1. 题目描述

https://leetcode-cn.com/problems/construct-quad-tree/
给你一个 矩阵 grid ，矩阵由若干 和 组成。请你用四叉树表示该矩阵 grid 。
你需要返回能表示矩阵的 四叉树 的根结点。
注意，当 isLeaf 为 False 时，你可以把 True 或者 False 赋值给节点，两种值都会被判题机制 接受 。
四叉树数据结构中，每个内部节点只有四个子节点。此外，每个节点都有两个属性：

• val：储存叶子结点所代表的区域的值。 对应 True， 对应 False；
• isLeaf: 当这个节点是一个叶子结点时为 True，如果它有 个子节点则为 False 。

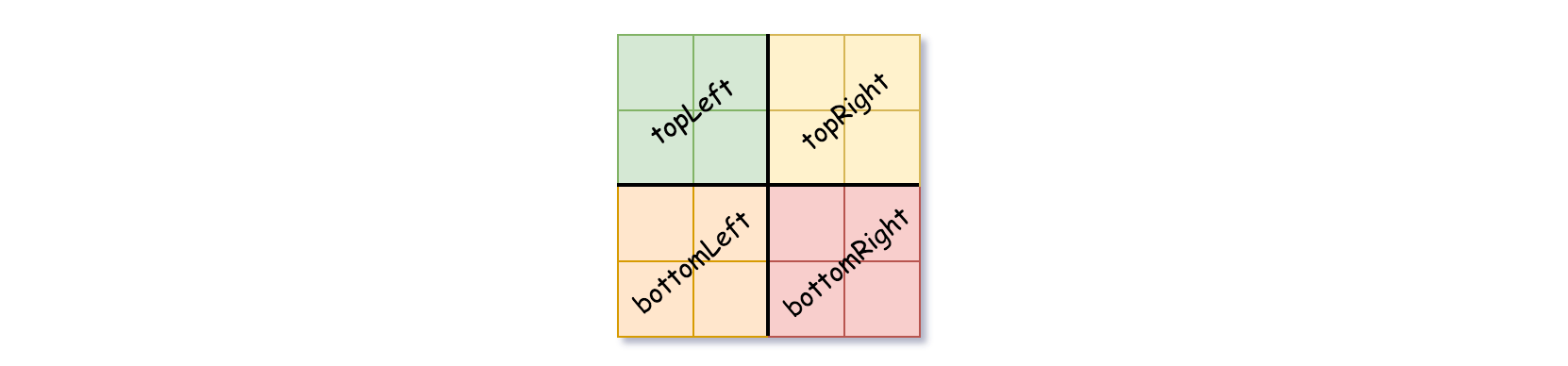
  class Node {
  public boolean val;
  public boolean isLeaf;
  public Node topLeft;
  public Node topRight;
  public Node bottomLeft;
  public Node bottomRight;
  }

  我们可以按以下步骤为二维区域构建四叉树：

1. 如果当前网格的值相同（即，全为 或者全为 ），将 isLeaf 设为 True ，将 val 设为网格相应的值，并将四个子节点都设为 Null 然后停止。
2. 如果当前网格的值不同，将 isLeaf 设为 False， 将 val 设为任意值，然后如下图所示，将当前网格划分为四个子网格。
3. 使用适当的子网格递归每个子节点。

四叉树格式：
输出为使用层序遍历后四叉树的序列化形式，其中 null 表示路径终止符，其下面不存在节点。
它与二叉树的序列化非常相似。唯一的区别是节点以列表形式表示 。
如果 isLeaf 或者 val 的值为 True ，则表示它在列表 中的值为 ；如果 isLeaf 或者 val 的值为 False ，则表示值为 。
示例 1：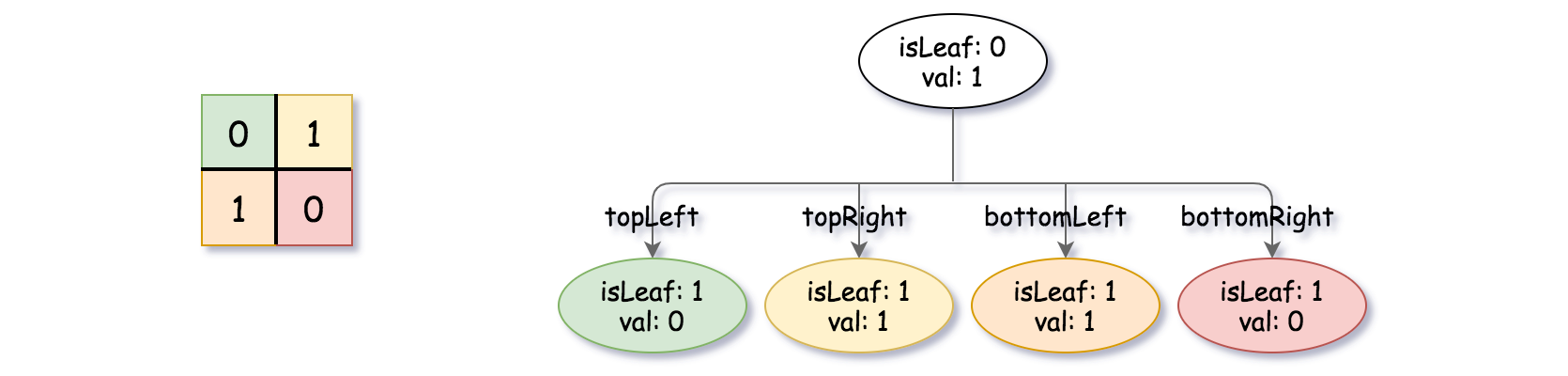

输入：grid = [[0,1],[1,0]]
输出：[[0,1],[1,0],[1,1],[1,1],[1,0]]
解释：请注意，在下面四叉树的图示中，0 表示 false，1 表示 True 。

示例 2：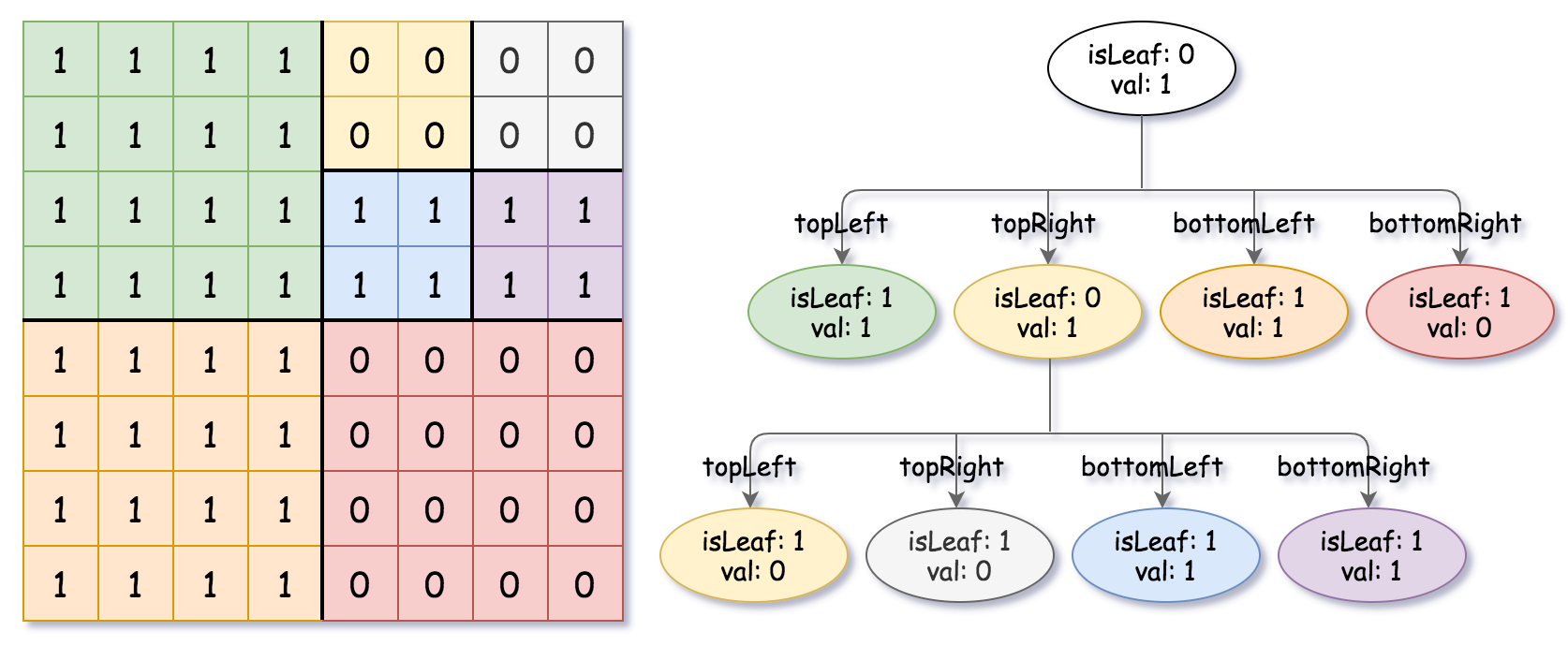

输入：grid = [[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,1,1,1,1],[1,1,1,1,1,1,1,1],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0]]
输出：[[0,1],[1,1],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]]
解释：网格中的所有值都不相同。我们将网格划分为四个子网格。
topLeft，bottomLeft 和 bottomRight 均具有相同的值。
topRight 具有不同的值，因此我们将其再分为 4 个子网格，这样每个子网格都具有相同的值。

示例 3：

输入：grid = [[1,1],[1,1]]
输出：[[1,1]]

示例 4：

输入：grid = [[0]]
输出：[[1,0]]

示例 5：

输入：grid = [[1,1,0,0],[1,1,0,0],[0,0,1,1],[0,0,1,1]]
输出：[[0,1],[1,1],[1,0],[1,0],[1,1]]

提示：

• 
• 其中

  2. 题解

  2022-04-29 AC, 初看起来完全懵逼, 不知道这个node节点到底怎么个输出法, 判断是否是子节点还行, 就是遍历一遍
  看了题解瞬间醍醐灌顶, 一个深搜, 主要就是生成新的四块区域, 这也是调试时间最长的地方 ```php <?php /**
  • Created by PhpStorm
  • User: jtahstu
  • Time: 2022/4/29 17:49
  • Des: 427. 建立四叉树
  • https://leetcode-cn.com/problems/construct-quad-tree/
  • 题目过长 */

//Definition for a QuadTree node. class Node { public $val = null; public $isLeaf = null; public $topLeft = null; public $topRight = null; public $bottomLeft = null; public $bottomRight = null;

function __construct($val, $isLeaf)
{
    $this->val = $val;
    $this->isLeaf = $isLeaf;
    $this->topLeft = null;
    $this->topRight = null;
    $this->bottomLeft = null;
    $this->bottomRight = null;
    echo "$isLeaf, $val\n";
}

}

class Solution { public $grid = [];

/**
 * @param Integer[][] $grid
 * @return Node
 */
function construct($grid)
{
    $this->grid = $grid;
    $n = count($grid);
    return $this->dfs(0, 0, $n - 1, $n - 1);
}

function dfs($a, $b, $c, $d)
{
    $is_leaf = true;
    $val = $this->grid[$a][$b];
    if ($a == $c && $b == $d) {
        return new Node($val, $is_leaf);
    }
    //判断矩形里的值是否都相同
    for ($i = $a; $i <= $c; $i++) {
        for ($j = $b; $j <= $d; $j++) {
            if ($this->grid[$i][$j] != $val) {
                $is_leaf = false;
                break 2;
            }
        }
    }
    //是子节点就不用再递归了
    if ($is_leaf) {
        return new Node($val, $is_leaf);
    }

    $node = new Node($val, $is_leaf);
    $g = ($a + $c + 1) / 2;  //x轴中点靠右
    $k = ($b + $d + 1) / 2;  //y轴中点靠右
    $node->topLeft = $this->dfs($a, $b, $g - 1, $k - 1);
    $node->topRight = $this->dfs($a, $k, $g - 1, $d);
    $node->bottomLeft = $this->dfs($g, $b, $c, $k - 1);
    $node->bottomRight = $this->dfs($g, $k, $c, $d);
    return $node;
}

}

(new Solution())->construct([[1, 1, 1, 1, 0, 0, 0, 0], [1, 1, 1, 1, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 0, 0, 0, 0], [1, 1, 1, 1, 0, 0, 0, 0], [1, 1, 1, 1, 0, 0, 0, 0], [1, 1, 1, 1, 0, 0, 0, 0]]); //(new Solution())->construct([[0, 1], [1, 0]]);

/**

• 执行用时：28 ms, 在所有 PHP 提交中击败了100.00%的用户
• 内存消耗：19.7 MB, 在所有 PHP 提交中击败了100.00%的用户
• 通过测试用例：22 / 22 */

/**

• 使用前缀和优化「判断全 0 和全 1」的操作
• 个人感觉速度也没快, 反而引入了额外的空间, 不如暴力^_^
• class Solution { static int[][] sum = new int[70][70]; int[][] g; public Node construct(int[][] grid) {

   g = grid;
   int n = grid.length;
   for (int i = 1; i <= n; i++) {
       for (int j = 1; j <= n; j++) {
           sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + g[i - 1][j - 1];
       }
   }
   return dfs(0, 0, n - 1, n - 1);
  

  } Node dfs(int a, int b, int c, int d) {

   int cur = sum[c + 1][d + 1] - sum[a][d + 1] - sum[c + 1][b] + sum[a][b];
   int dx = c - a + 1, dy = d - b + 1, tot = dx * dy;
   if (cur == 0 || cur == tot) return new Node(g[a][b] == 1, true);
   Node root = new Node(g[a][b] == 1, false);
   root.topLeft = dfs(a, b, a + dx / 2 - 1, b + dy / 2 - 1);
   root.topRight = dfs(a, b + dy / 2, a + dx / 2 - 1, d);
   root.bottomLeft = dfs(a + dx / 2, b, c, b + dy / 2 - 1);
   root.bottomRight = dfs(a + dx / 2, b + dy / 2, c, d);
   return root;
  

  } } */ ```