学习目标

• 掌握5个命题连接词的运算规律

• 对符合命题符号化

  1. 命题的基本概念

• 在数理逻辑中把能判断真假的陈述句称为命题

• 一般用小写英文字母或者小写英文字母带下标表示
• 命题的概念包含了以下2个要素(缺一不可)
  • 陈述句
  • 能判断真假

    【判断题】判断以下语句是否为命题。若是命题，确定其真值。

1. 上海是个小村庄。 判断：1.是陈述句 2.上海为大城市 结论：是命题 真假值为假 F
2. 存在外星人。 判断：1.是陈述句 2.有没有外星人非真既假 结论：是命题 T
3. 禁止吸烟！ 判断：1.是感叹句 结论：命题为陈述句，且有真假值，所以不是命题
4. 北京是中国的首都。 判断：1.是感叹句 2.结果为真 结论：是命题，结果为真 F
5. 4是素数或6是素数。 判断：1.由或链接的两个陈述句 2.4和6都不是素数，结论：是命题 结果为假 F
6. 今天你吃了吗？ 判断：1.是疑问句 结论：不是命题
7. 11+1=100 判断：1.是陈述句 结论：结果为假F
8. 我正在说谎。 判断：1.是陈述句 2.结果不能判断真假值 结论：不是陈述句，被称为悖论

   2. 命题联结词

• 北京是中国的首都。不可以再分解——原子命题。
• 4是素数或者6是素数。可分解为4是素数 6是素数 两个命题构成的复合命题。
• 如果一个命题不能再分解成为更简单的命题，则称该命题为原子命题。
• 如果一个命题可以分解为多个原子命题，称该命题啊为复合命题。
• 复合命题中的原子命题是用联结词来连接的。
• 通常用符号(英文字母，大小写皆可，也称为命题标识符)来表示一个命题，这个过程称为命题的符号化。

• 符号化时要考虑一下因素：

  • 某个特定的命题的命题标识符称为命题常量或命题长项。
  • 如果命题标识符只表示命题的位置(可代表不同的命题)，则称其为命题的变元或命题变项。
  • 联结词的表示

    2.1 常用的命题联结词有五种

  1. 否定联结词(一元的联结词)
  2. 合取联结词
  3. 析取联结词
  4. 条件联结词
  5. 双条件联结词

     2.2 否定联结词

     定义：假设为命题，则的否定是一个复合命题，记作：，读作非或。定义为：。其真值表如下表所示：
     

     2.3 合取联结词

定义：假设和均为命题，则的合取是一个复合命题，记作：，读作
。定义为：当且仅当，其真值表如下表所示：

• 例：
  • 1. 4是偶数，6也是偶数。

解：
命题：
这是一个合取的复合命题，结果为真

• 1. 4和6都是偶数

解：这里的和连接的是4,6，他们整体作为一个要说明的对象，所以该题目为一个原子命题。

2.4 析取联结词

定义：假设，记作：,读作：。定义当且仅当。其真值表如下表所示：

• “或”的两种不同含义
  1. 同或：表示相容，描述的两个命题并不排斥，可以同时发生。（析取对应的是同或）
     • 例：
  2. 异或：表示相斥，描述的两个命题不可以同时发生时成立(为真)
     • 例：

       2.5 条件联结词

       定义：假设其条件命题是复合命题，记为：,读作“如果”或“”,当且仅当时，才为假，为条件命题：的后件。其真值表如下所示：

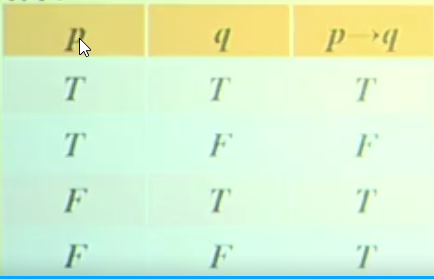
• 例：设则命题：如果小王努力学习，那么他的学习成绩就优秀，可以符号化为：。