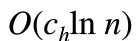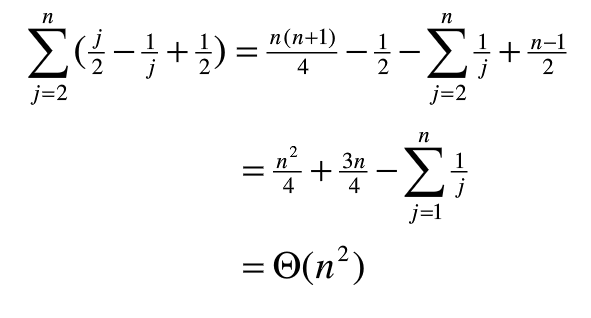1. 概率分析
- 平均案例分析决定算法运行平均时间
- 期望运行时间往往是所有n个实例运行时间的平均
- 平均情况分析往往需要对事件的先验概率有一个较好的估计
- 精确的时间复杂度分析往往耗时耗力
如果你对平均情况更为感兴趣,name可以考虑使用概率分析,并在这一过程中,认为每种情况都等可能的发送
2. The linear search problem
Search an array A of size n to determine whether the array contains the value x; return index if found, 0 if not found
LinearSearch(A,x)k = 1while (k <= n) and < (x != A[k]) dok++if k > n then return 0else return k
好差复杂度:n
- 最好情况:1
- 循环不变量:当n=k时x还没有出现在前k-1个元素中
- 为了简化分析,让我们假设A[1…n]包含数字1到n,这意味着A的所有元素都是不同的
- 平均状态下的查找:
- 对于k的每个值,在索引k出找到的x的概率是1/n
- 如果x=A[k],那么比较的数量是k
- 因此,通过LinearcSearch(A,x)来找到x的位置需要比较次数的期望为:
这表明该算法的平均执行时间为
个元素比较以定位x,因此算法的平均时间复杂度为
3. 用于排序问题的InsertSort(A)
考虑InsertSort(A)中进行的所有比较,为了简化分析,我们假设A[1…n]包含数字1到n,这意味着A的所有元素都是不同的。
- 让我们假设所有n!种全排列等可能出现。现在我们考虑将key=A[j]插入到A[1…j]中的正确位置。如果其正确位置是k
,那么为了将A[k]插入其正确位置而执行的比较次数是j-k+1次,如果j=2
,怎为j-k次。由于在A[1…j]中的适当位置的概率为,因此在A[1…j]中将A[j]插入其实当位置所需要比较的次数为:推导过程,自行推导,可以画图协助
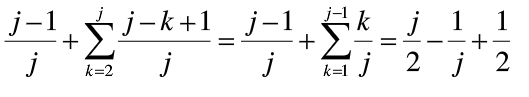
- 所以InsertSort(A)的平均比较次数为:
4. 雇佣问题
假设需要招聘新的办公室助理。如果被招聘的人比现任的助理能力强,就解聘现任的助理,启用新招聘的助理,否则则就从新招聘。需要支付的解雇费用和招聘费用如下:
HireAssistant(n)best = 0for i = 1 to n dointerview candidate iif candidate i is better than candidate best thenbest = ihire candidate i
面试费用
,雇佣费用较高,为
.假设雇佣m个人,name该算法对应的总花费为
。
- 最差情况:
应聘者一个比一个能力请
- 最好的情况
雇佣问题概率分析
- 对于雇佣问题,我们假设应聘者以随机的顺序来应聘,假设我们能够对比两个应聘者的能力的高低,name就能够确定是否雇佣该应聘者。
- 雇佣问题分析
- 候选人被雇佣的概率
- 雇佣费用
- 雇佣的平均费用为:
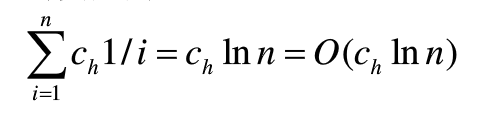
- 候选人被雇佣的概率
- 引理
当雇佣者以随机顺序来应聘时。算法的总雇佣花费为: