1. 矩阵是什么

1.1问题引入

1.1.1 基础条件

1.1.2 信息描述

1.1.3 问题

1.1.4 问题求解

1.2 矩阵

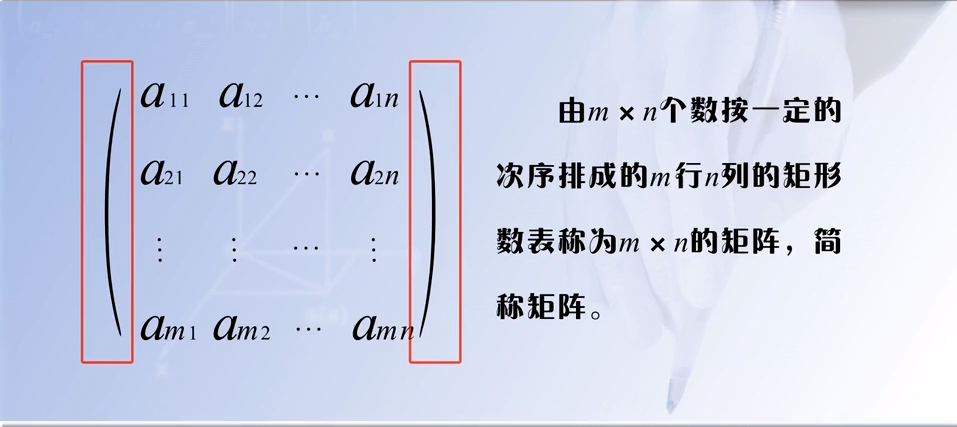
1.2.1 矩阵的定义，矩阵的符号是圆扩符

1.2.2 矩阵的行、列和元素

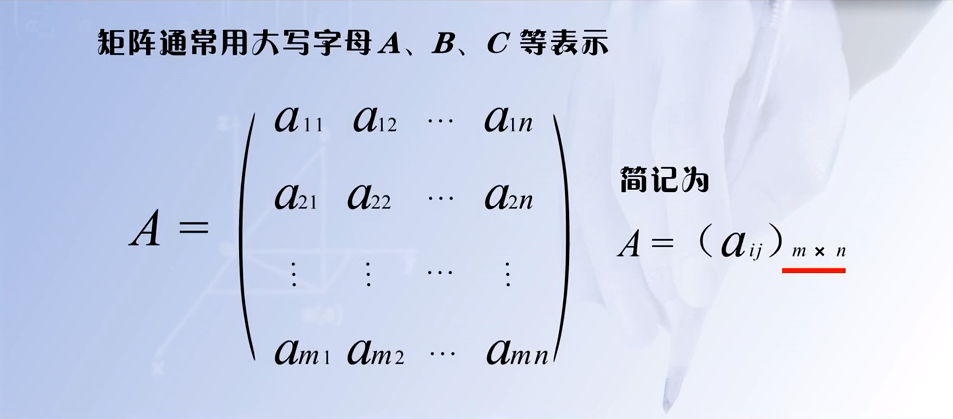
1.2.3 矩阵的表示

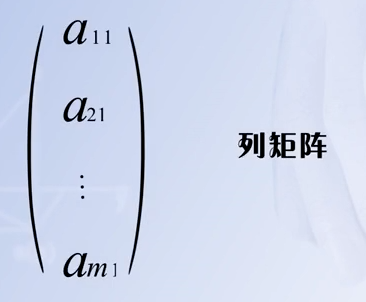
1.2.4 行矩阵和列矩阵

2. 几种特殊的矩阵

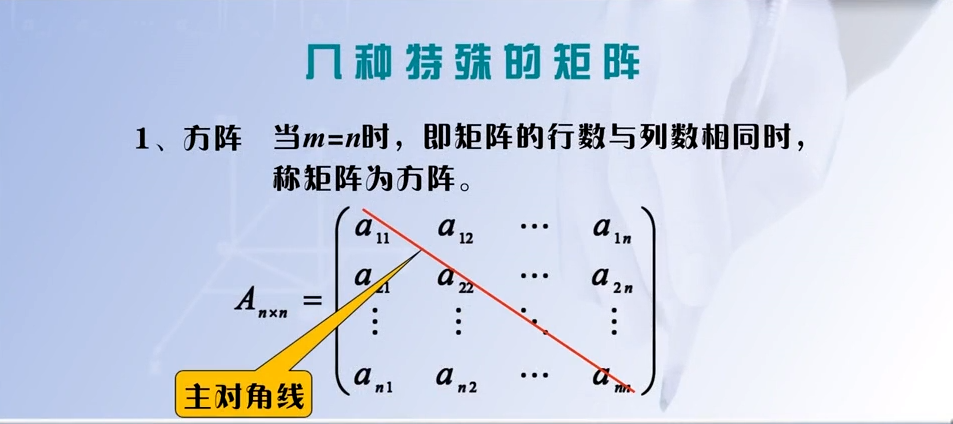
2.1 方正

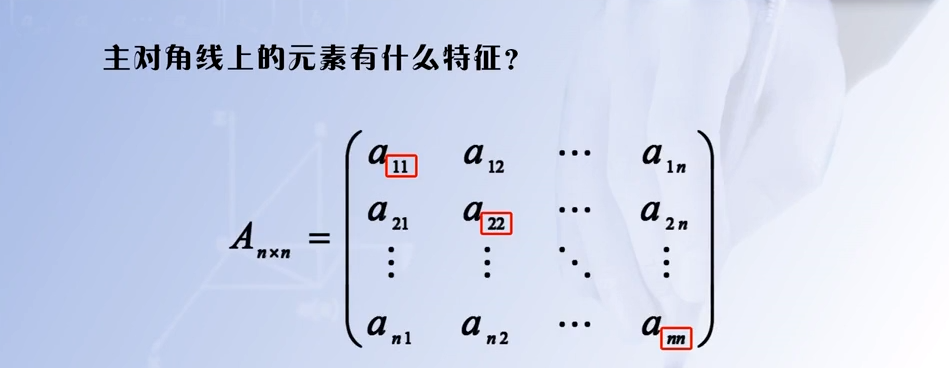
2.1.1 主对角线元素的特征

2.2.2 不是方阵能有主对角线吗

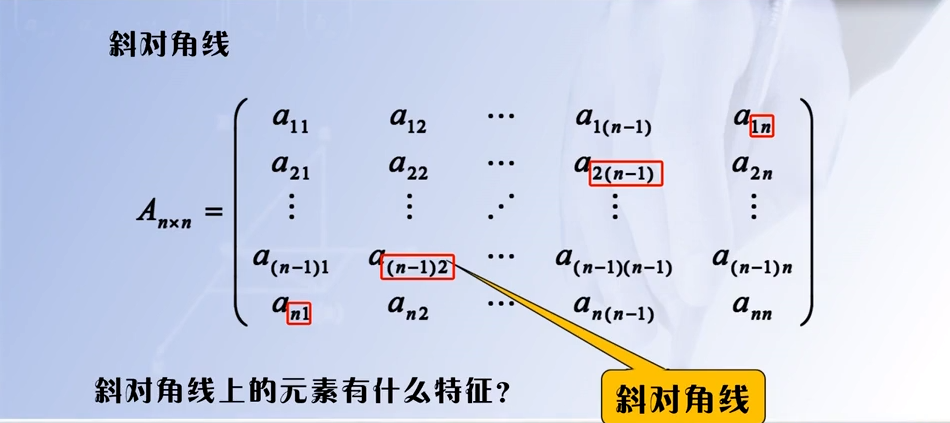
2.2.3 斜对角线

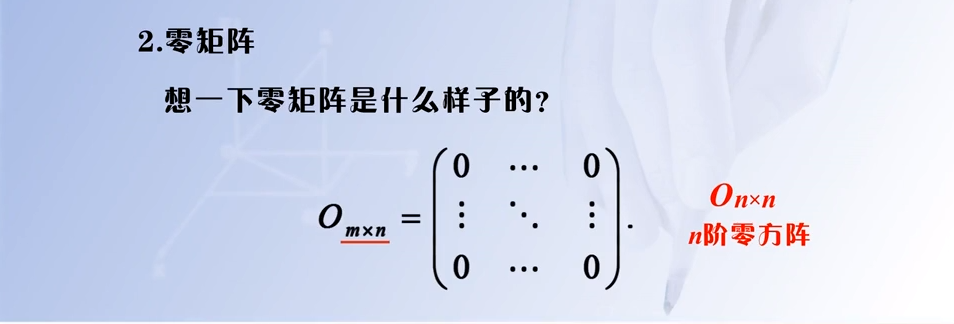
2.2.4 零矩阵

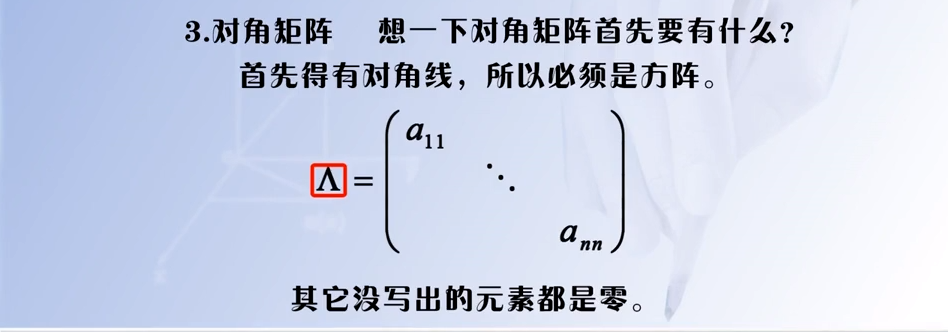
2.2.5 对角阵

2.2.6 单位阵

2.2.7 数量阵

对角阵、单位阵、数量阵的共同点

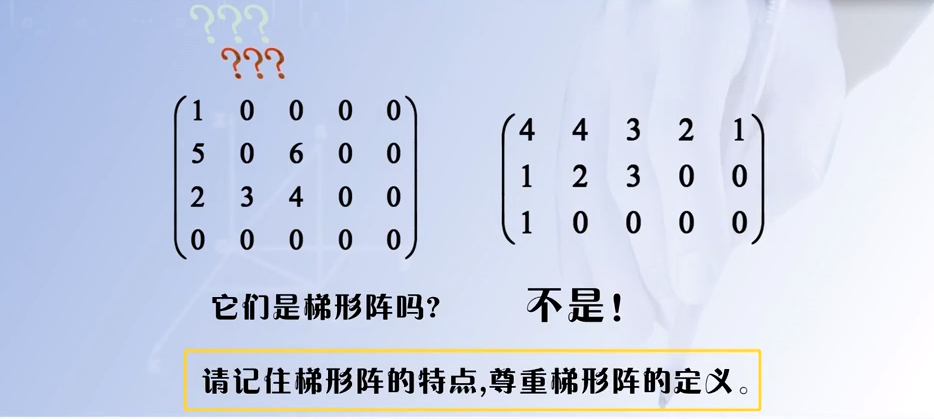
2.2 梯形阵

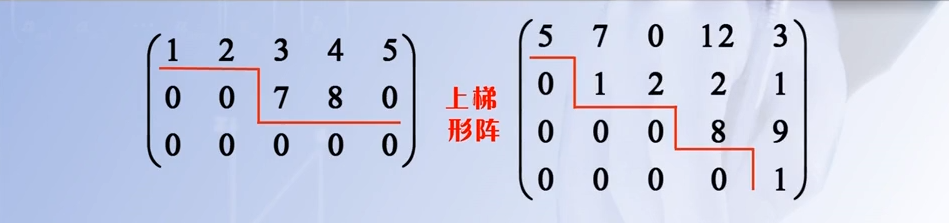
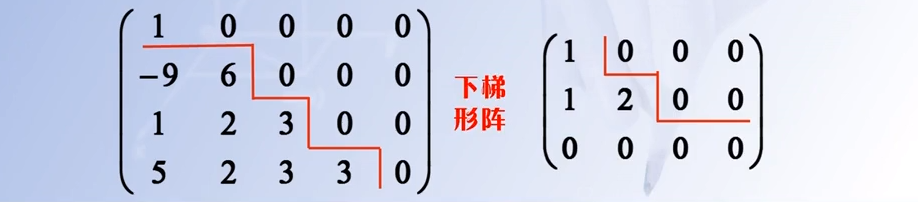
2.2.1 例

上梯形阵，零元素的个数在增加

下梯形阵，零元素的个数在减少

注意：没有说零元素的个数需要增加多少，或减少多少，只要有增加或减少就行

2.2.2 判断梯形阵