对于DFS，在leetcode中的应用场景大多数都是关于二叉树或者二维表格（或者图）所表示的题目，因为二叉树的遍历本身就是一个DFS的过程，并且很多题目，不论是统计某个数值还是还原二叉树等等都是依托于二叉树的遍历的，但今天所谈的这个DFS是与记忆化所结合的，它一般可以应用于能用含有重叠子问题的题目，比如说大部分动态规划题目，其实也可以由DFS+记忆化来解答。下面这道题目，在leetcode中分类为动态规划，我们尝试用DFS+记忆化来求解。

1. 不同的二叉搜索树

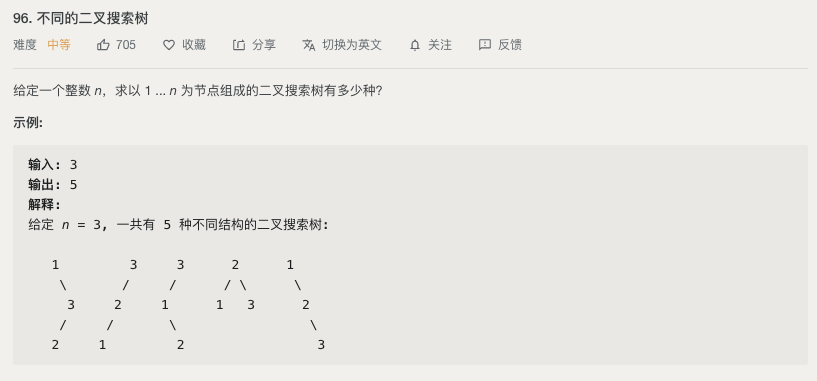
image.png
乍一看这题颇有回溯的意味，回溯其实也算作暴力破解吧。而回溯的过程可以构建出一棵递归树，实际上这棵树我们使用dfs也能构建出来，也就是说这些算法本质上没有太大区别，都是基于递归实现的，甚至中间产物都一样；只不过各自有各自强调的点，比如说回溯强调 ”回“ , DFS强调”深度优先“。而对于这题，明显是没有强调”回”这个点的。
比如说我们要求 n = 3时，以2为根节点能构成的二叉搜索树的数目。很明显，输入的是一个数字，那我们可以产生一个 “实际上不存在” 的有序序列 [1,2,3] ,这也是我们无需多关注所构建的树是否是二叉搜索树的原因。按照二叉搜索树的特性，根节点的左子树一定比根节点小，右子树比根节点大，所以序列中比2小的[1]可以构成左子树，比2大的[3]可以构成右子树，而所生成的左子树的种类 乘上所生成的右子树的种类就是最终以2为根节点的二叉搜索树的数量。
翻译成伪代码。

  1. num_root2 = count(1,1) * count(2,3)   //其中count函数是计算区间[start,end]所能构成的平衡二叉树数量

是不是有递归，或者dfs的味道了。
在DFS或者动态规划的问题中，子问题和最终问题都是平级的，所运行的代码，所执行的转移方程都是一样的。这也为我们接下来写代码提供了支撑。我们要求的是1…n所构成的二叉搜索树的数量，既然刚才的算法是求解根节点为2的二叉搜索树的数量，那我们不妨让每一位，都当一把根节点，体会当”祖先”的乐趣。

  1. int num = 0;
  2. for(int i = 1;i <= n; i++){
  3.      num += count(start,i-1) * count(i+1,end);    
  4. }
  5. return num;

到这里就结束了。你不必考虑子问题是怎么计算的，因为他们的逻辑和最终问题的逻辑是一样的，如果不一样，也别想着用这种方法解题。顾全大局即可。

递归问题，切忌刨根问底。

  1. fun dfs(start: Int, end: Int): Int {
  2.     if (start >= end) return 1
  3.     var sum = 0
  4.     for (i in start..end) {
  5.         sum += dfs(start, i - 1) * dfs(i + 1, end)
  6.     }
  7.     return sum
  8. }

这个代码就是最终的代码。只不过用kotlin重写了一下，然后加上了递归终止条件，在序列只剩一个元素或者不剩的时候默认返回1,(注意不能返回0，乘以0可就啥也没了)

2. 记忆化


不出意外，上面的代码已经超时警告了。
在动态规划-重叠子问题我已经提到过了，如果使用单纯的DFS或者递归必然会产生大量重叠子问题，这个题目也不例外。只要有重叠子问题，我们都可以利用记忆化或者动态规划来解决。而所谓的记忆化，无非就是把已经求得结果的子问题的结果记录下来，下次再遇到他的时候，可以直接取值。这样的键值对策略，一般是选用HashMap啦。

  1. val memo = HashMap<String, Int>()
  2. fun dfs(start: Int, end: Int): Int {
  3.     if (start >= end) return 1
  4.     var sum = 0
  5.     for (i in start..end) {
  6.         val left = if (memo.containsKey("$start,${i - 1}")) {
  7.             memo["$start,${i - 1}"]!!
  8.         } else {
  9.             val result = dfs(start, i - 1)
  10.             memo["$start,${i - 1}"] = result
  11.             result
  12.         }
  13.         val right = if (memo.containsKey("${i + 1},$end")) {
  14.             memo["${i + 1},$end"]!!
  15.         } else {
  16.             val result = dfs(i + 1, end)
  17.             memo["${i + 1},$end"] = result
  18.             result
  19.         }
  20.         sum += left * right
  21.     }
  22.     return sum
  23. }

代码中添加了memo这个HashMap来缓存值，key可以随意取，保证能唯一标示一个子问题即可

但是注意不要取引用类型，数组，等等这种。因为某些类型HashCode不一定重写过，而且自定义引用类型如果HashCode没有重写过也会出问题。所以用最简单的字符串是非常好的。


这里用了 "$start,${i - 1}" 类似于这样的一个字符串作为key，这个东西在Kotlin中叫做字符串模板，实际上编译出来就是 start的值,i-1的值 编译器会将 $描述的量全部替换为他的真实值，也就是，我们将起始点和终止点拼接在一起作为唯一标识，这也是我们dfs函数的签名，我们用一个start和一个end就可以唯一确定一个子问题。
下面的代码就很好理解了，只需要读字面意思即可，如果取不到当前子问题的值，就计算，计算完成之后加入到Map中。这样我们可以免去很多重叠子问题的计算问题。

3. 总结

其实也谈不上什么理解，只是这是一个在不会动态规划解法时候的一个”备选方案”。通常情况下，我们也较容易想到的也是DFS + 记忆化的解法，再一步步转换为动态规划。而且在此类题目场景下，一般是DFS和记忆化是配套出现的，复杂情况可能会配合一些剪枝操作，如动态规划-重叠子问题中将数字翻译成字符串中就包含对一些不可能的分支进行剪枝。

本文就到这里啦，有点短。后面可能再补充一个例题。可以结合动态规划系列来理解这个问题。