最近在进行Leetcode每日一题打卡活动中，遇到不少关于海岛的问题，这些问题有Easy也有Hard，但是大致的套路都涉及到网格遍历，或者直截了当的说，都是DFS（深度优先遍历）或者BFS（广度优先遍历，后边直接使用简称）的基础应用，在此之前，我经常应用到的是树的BFS，也可以说成单源BFS，是一个初始时候只有一个节点的遍历过程。而对于网格的遍历情况就比较复杂，有些题型单源BFS无法实现，就必须借助于多源BFS。
image.png
真的学不会么？因为没掌握核心思想罢了。
下面就从几个方面来分析BFS的基础框架以及面对海岛类问题如何用BFS实现。

前言

首先我们可以看一道题目，是一道middle的岛屿题目：岛屿的最大面积.

给定一个包含了一些 0 和 1 的非空二维数组 grid 。 一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为 0 。)示例 1:> [[0,0,1,0,0,0,0,1,0,0,0,0,0], [0,0,0,0,0,0,0,1,1,1,0,0,0], [0,1,1,0,1,0,0,0,0,0,0,0,0], [0,1,0,0,1,1,0,0,1,0,1,0,0], [0,1,0,0,1,1,0,0,1,1,1,0,0], [0,0,0,0,0,0,0,0,0,0,1,0,0], [0,0,0,0,0,0,0,1,1,1,0,0,0], [0,0,0,0,0,0,0,1,1,0,0,0,0]]

对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ，因为岛屿只能包含水平或垂直的四个方向的 1 。

对于上面的题目，我们可以提取关键思想。
1 是陆地，0是海洋，如果一堆1聚集在一起可以形成一个岛屿（斜相邻不算），求给定二维数组中最大岛屿的面积。为了帮助理解，我这里给一个更简单的例子。
image.png
对应上面的4 * 5数组，海岛主要分为3块，也就是红色框框出来的三块，而我们的目标就是要求出这三块其中最大的一块面积，在上面的图示中，最大面积是左边和下边的这两块，值为4。对于求4这个值，自然而然的会想到要遍历这些区域，累加求和求一个最大的。

这只是其中一个题目，相似的题目还有很多，那么我们怎么运用BFS来解决这些问题呢？

BFS基本框架

二叉树的BFS框架

我们都知道二叉树的BFS，也就是二叉树的层序遍历，伪代码如下。

  1.   void bfs(TreeNode treeNode){
  2.         LinkedList<TreeNode> queue = new LinkedList<>();
  3.         queue.offerLast(treeNode);
  4.         while (!queue.isEmpty()){
  5.             TreeNode node = queue.pollFirst();
  6.             System.out.println(node.val);
  7.             if(node.left != null)queue.offerLast(node.left);
  8.             if(node.right != null)queue.offerLast(node.right);
  9.         }
  10.   }

很简单的几步，一步一步来说。

  • 首先使用LinkedList作为队列，BFS的核心就在于这个队列。这里LinkedList是实现了Queue的接口的，可以作为队列使用。
  • 然后将最开始的节点入队。
  • 接下来是一个while，如果队列不为空就一直执行，从队列中取队首节点，将其打印（也可以换做其他操作）,然后将其合法的子节点入队。

这样简单的3步，我们就实现一个BFS操作。

你能从这3步中总结出什么？
image.png
虽然上面的代码寥寥几行就可以实现一个“复杂操作”，但其中也不乏一些关键位置。如下面这两点

  1. 访问相邻合法节点

上面的代码中
image.png
这两行是对当前节点的相邻节点的合法访问，何为相邻，在树里，某节点的孩子节点都为他的“相邻节点”，那何为合法节点，在树里，合法就是不为null

  1. 对当前节点进行操作

这一步是解题的关键，大部分题目都是需要对遍历的内容进行操作或者统计的，掌握它的位置和使用时机，灵活运用这一步操作就可以搞定题目啦。

二维网格的BFS模板

上面总结了二叉树的BFS模板，并且发现了2个核心的点，这时候我们就可以通过这些已经get到的内容总结出二位网格的BFS模板，不过在出代码之前，我们还是一起来跟着图学习一下。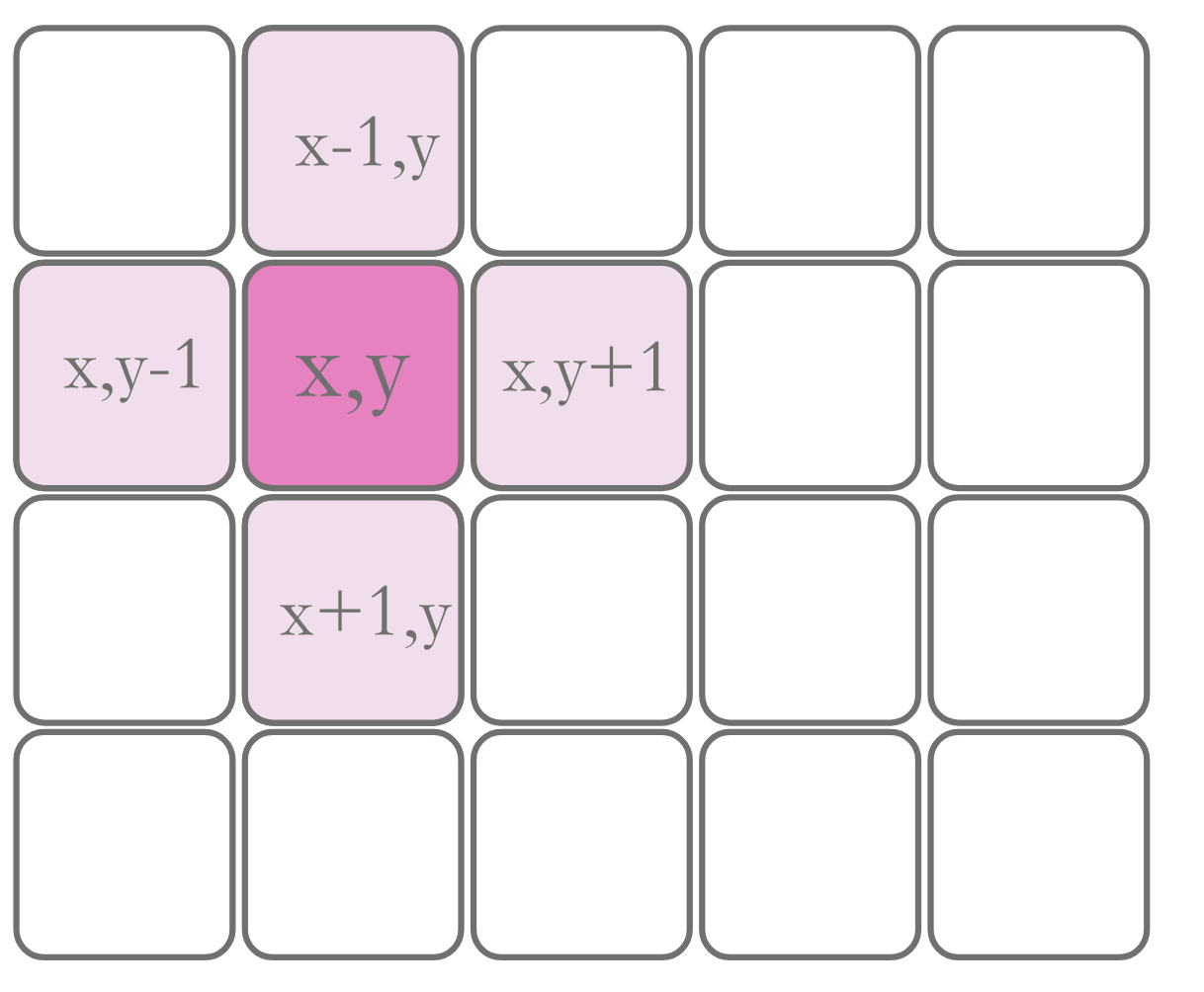
image.png
上面我们提到的两点这么快就要复习了。
第一点，访问相邻合法节点，在图中相邻指的是什么？通常是指某节点上下左右4个位置，当然也不乏“八卦”，所有环绕节点都包括这种，解决海岛问题，一般使用4个位置即可。如上图(x,y)的相邻节点就是周围4个浅粉色的格子。那什么叫做合法呢？这就要上下一张图了。

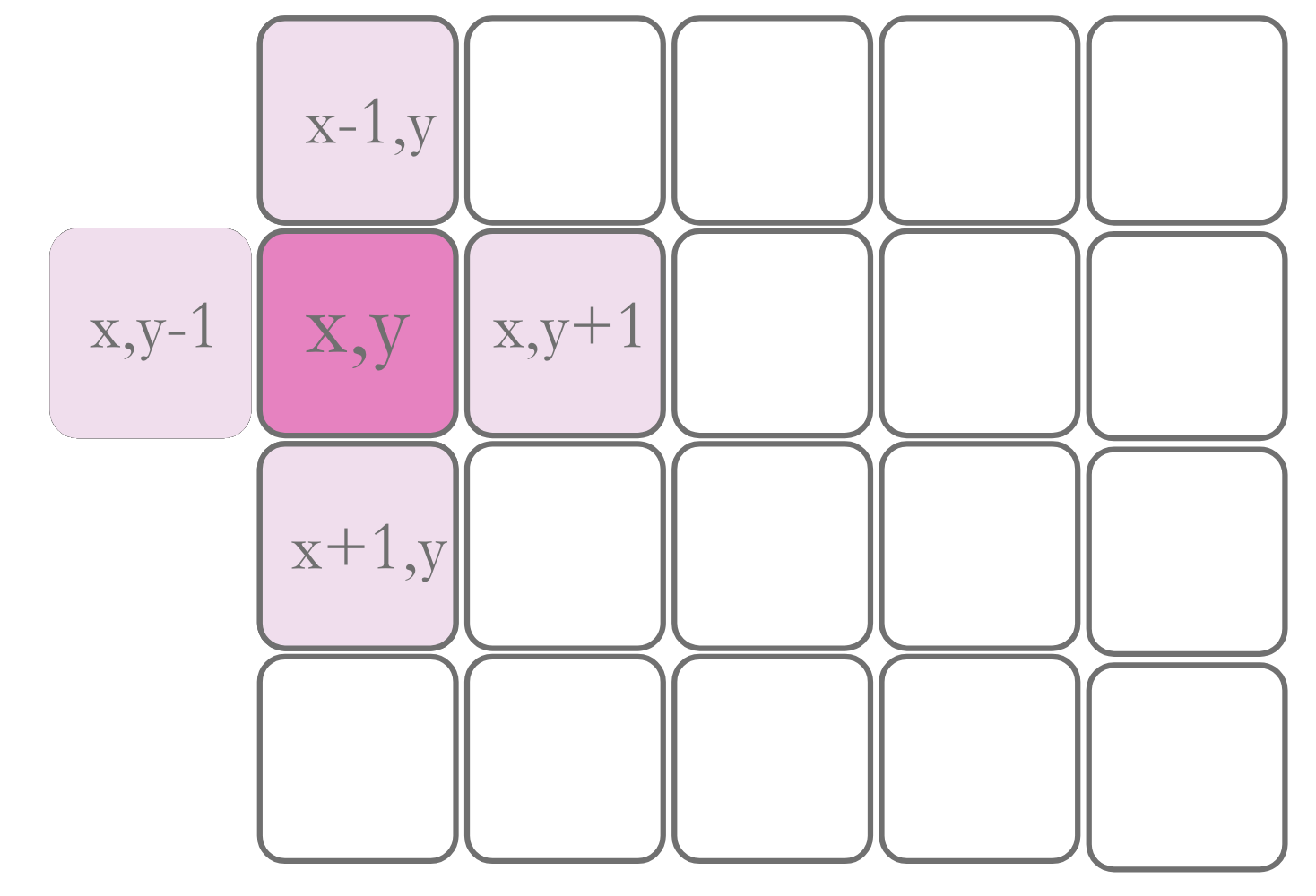
image.png
在这张图中，(x,y)是边界上的一个点，它的上下和右都在矩阵中，但是左边不在了，如果我们依然访问它左边的节点，就会产生越界异常，这可不是我们想要的，所以左边的节点不是一个合法的节点，在算法执行过程中，需要被忽略掉。

第二点，对当前节点进行操作
前面说过，解决海岛类问题或者其他BFS的问题的关键就是在该处理的地方进行处理，当BFS运算结束之后就可以得到答案。那么对于开篇引入的问题，我们需要做的操作是什么? 当然是“统计面积” 题目都说了。面积是什么？即某个陆地相邻的合法陆地的数目。所以在每次取出节点的时候都要统计面积。
image.png
这里的Point是用作记录节点位置的。
掌握这两点就结束了吗？不妨写写看。首先给出一个伪代码。

  1.  void bfs(int[][] nums) {
  2.         Queue queue = new Queue();
  3.         queue.push(Node(0, 0));
  4.         while (!queue.isEmpty()) {
  5.             Node node = queue.poll();
  6.             if (isInArray(node.x - 1, node.y)) queue.push(Node(node.x - 1, node.y));
  7.             if (isInArray(node.x + 1, node.y)) queue.push(Node(node.x + 1, node.y));
  8.             if (isInArray(node.x, node.y - 1)) queue.push(Node(node.x, node.y - 1));
  9.             if (isInArray(node.x, node.y + 1)) queue.push(Node(node.x, node.y + 1));
  10.         }
  11.   }

上面的代码就是一个最初的版本，那你认为这样就可以了吗？

image.png
然后执行后 ……TLE警告。
产生超时的原因并不是复杂度搞，而是代码有问题。继续看这张图，我们会发现（x,y）这个点，四个相邻的位置依此被入队，然后读取他们的时候，他们四个相邻的位置又被依此入队，但此时我们会发现（x,y）这家伙又来了一遍，所以这样就会产生死循环。肯定会超时。
image.png
那么这应该怎么处理呢？正确答案是将他们列为不合法的行列。使用访问标志位将访问过的标志都标记，这样下次访问的时候，读到标记的时候就可以直接跳过。

image.png
下面就给出最终版！BFS的核心模板。

  1.  void bfs(int[][] nums) {
  2.         int xLen = nums.length;
  3.         int yLen = nums[0].length;
  4.         int[] x = new int[]{-1, 1, 0, 0};
  5.         int[] y = new int[]{0, 0, -1, 1};
  6.         LinkedList<Point> queue = new LinkedList<>();
  7.         queue.offerLast(new Point(0, 0));
  8.         while (!queue.isEmpty()) {
  9.             Point point = queue.pollFirst();
  10.             System.out.println(point);
  11.             for (int i = 0; i < 4; i++) {
  12.                 int curX = point.x + x[i];
  13.                 int curY = point.y + y[i];
  14.                 //如果产生的越界，就跳过本次
  15.                 if (curX < 0 || curX >= xLen || curY < 0 || curY >= yLen) continue;
  16.                 //如果已经访问过，就跳过本次
  17.                 if (nums[curX][curY] == Integer.MIN_VALUE) continue;
  18.                 //否则就入队
  19.                 queue.offerLast(new Point(curX, curY));
  20.                 //将此节点标志为已访问
  21.                 nums[curX][curY] = Integer.MIN_VALUE;
  22.             }
  23.         }
  24.     }

貌似有点长，而且这里我换了另一个写法访问周围4个节点。x数组和y数组的对应位置分别对应了上（-1,0）、下（1,0）、左（0，-1）、右（0，1）四个位置，访问的时候，直接用某节点的x,y坐标与之进行加法运算就可以求得4个临接点。而且这样我们只需要写一个越界判断即可，产生错误就continue，接下来判断该位置是否已经被访问，被访问的节点也跳过。节点合法后入队，并且标记为已访问位。

使用BFS模板解决海岛类问题

首先当然是解决刚才我们提及到的问题。

岛屿的最大面积

刚才已经说过，要知道题目要求求解什么。求岛屿的最大面积，当然是将所有的岛屿的面积求出来再取最大值。所以我们至少会根据上面的条件写出下面两行。

int ans = 0; ans = Math.max(ans,下一个岛屿的最大面积);

有了这两行我们就要考虑下一个问题了，max方法里面有一个下一个岛屿的面积，所以我们的问题就是怎么找到下一个岛屿？这个没什么好办法，就是遍历去找。找到一个1就认为他是一个岛屿的一部分，由他来展开搜索更大的陆地块，由于陆地块访问后会被我们标记，所以不用担心重复计算。那么接下来就是一个双层遍历。

我在这里遍历二维矩阵查找一个1，然后就是上面我们提到的求最大的方法。
当然，求下一个岛屿的最大面积就是BFS模板咯

  1. int result = 0;
  2.         for (int i = 0; i < grid.length; i++) {
  3.             for (int j = 0; j < grid[i].length; j++) {
  4.                 if (grid[i][j] == 1) {
  5.                     result = Math.max(result, findIsland(grid, i, j));
  6.                 }
  7.             }
  8.         }
  9. return result;

然后就是综合的代码。

  1.  public int maxAreaOfIsland(int[][] grid) {
  2.         int result = 0;
  3.         for (int i = 0; i < grid.length; i++) {
  4.             for (int j = 0; j < grid[i].length; j++) {
  5.                 if (grid[i][j] == 1) {
  6.                     int a = 0;
  7.                     result = Math.max(result, (a = bfs(grid, i, j)));
  8.                 }
  9.             }
  10.         }
  11.         return result;
  12.     }
  15.     int bfs(int[][] nums, int sX, int sY) {
  16.         int ans = 0;
  17.         int xLen = nums.length;
  18.         int yLen = nums[0].length;
  19.         int[] x = new int[]{-1, 1, 0, 0};
  20.         int[] y = new int[]{0, 0, -1, 1};
  21.         LinkedList<Point> queue = new LinkedList<>();
  22.         queue.offerLast(new Point(sX, sY));
  23.         nums[sX][sY] = 2;
  24.         while (!queue.isEmpty()) {
  25.             Point point = queue.pollFirst();
  26.             ans++;
  27.             for (int i = 0; i < 4; i++) {
  28.                 int curX = point.x + x[i];
  29.                 int curY = point.y + y[i];
  30.                 //如果产生的越界，就跳过本次
  31.                 if (curX < 0 || curX >= xLen || curY < 0 || curY >= yLen) continue;
  32.                 //如果已经访问过，就跳过本次,此外0是海域，也不能算作内
  33.                 if (nums[curX][curY] == 2 || nums[curX][curY] == 0) continue;
  34.                 //否则就入队
  35.                 queue.offerLast(new Point(curX, curY));
  36.                 //将此节点标志为已访问
  37.                 nums[curX][curY] = 2;
  38.             }
  39.         }
  40.         return ans;
  41.     }
  44.     static class Point {
  45.         public int x;
  46.         public int y;
  47.         public Point(int x, int y) {
  48.             this.x = x;
  49.             this.y = y;
  50.         }
  51.     }

上面代码基本上跟之前的一样。有几个小点进行了修改。

  • BFS模板的代码添加了返回值，用于返回当前陆地的面积，使用了一个ans变量统计面积，每次从队列中取数据都会自增。
  • 对于0所表示的海域不能算作在内，所以当发现某个值是0的时候，也要跳过。

这样看起来，分析这样一道题只需要2步，一是找到何时开始用BFS，二是用BFS的过程中需要添加哪些内容。

有了这道题目的经验，再来类似的题目也不怕啦。

岛屿数量

给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

输入: 11000 11000 00100 00011 输出: 3 解释: 每座岛屿只能由水平和/或竖直方向上相邻的陆地连接而成。

我想说，这完全一样好吧。
这个题目比上面的简单点，首先我们不用统计bfs的结果了，所以我们对模板又进行了改造，数组换成了题目要求的char类型，标志位，海域等标记都更新成了char类型。

  1.   void bfs(char[][] nums, int sX, int sY) {
  2.         int xLen = nums.length;
  3.         int yLen = nums[0].length;
  4.         int[] x = new int[]{-1, 1, 0, 0};
  5.         int[] y = new int[]{0, 0, -1, 1};
  6.         LinkedList<Point> queue = new LinkedList<>();
  7.         queue.offerLast(new Point(sX, sY));
  8.         nums[sX][sY] = '2';
  9.         while (!queue.isEmpty()) {
  10.             Point point = queue.pollFirst();
  11.             for (int i = 0; i < 4; i++) {
  12.                 int curX = point.x + x[i];
  13.                 int curY = point.y + y[i];
  14.                 //如果产生的越界，就跳过本次
  15.                 if (curX < 0 || curX >= xLen || curY < 0 || curY >= yLen) continue;
  16.                 //如果已经访问过，就跳过本次
  17.                 if (nums[curX][curY] == '2' || nums[curX][curY] == '0') continue;
  18.                 //否则就入队
  19.                 queue.offerLast(new Point(curX, curY));
  20.                 //将此节点标志为已访问
  21.                 nums[curX][curY] = '2';
  22.             }
  23.         }
  24.     }
  27.     public int numIslands(char[][] grid) {
  28.         int ans = 0;
  29.         for (int i = 0; i < grid.length; i++) {
  30.             for (int j = 0; j < grid[i].length; j++) {
  31.                 if (grid[i][j] == '1') {
  32.                     ans++;
  33.                     bfs(grid,i,j);
  34.                 }
  35.             }
  36.         }
  37.         return ans;
  38.     }
  41.     static class Point {
  42.     public int x;
  43.     public int y;
  45.         public Point(int x, int y) {
  46.             this.x = x;
  47.             this.y = y;
  48.         }
  49.     }