leetcode-121-买卖股票的最佳时机，这是一道easy题目，至于说他easy因为这道题目”看起来”很简单,也很容易想到暴力破解的方案。但其实这个题目有n多种解法，如DP等，具体的几种方法，在下面列举一下。

题目

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票一次），设计一个算法来计算你所能获取的最大利润。

注意：你不能在买入股票前卖出股票。

示例 1:

输入: [7,1,5,3,6,4]

输出: 5

解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。

  1. 注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。

示例 2:

输入: [7,6,4,3,1]

输出: 0

解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock

著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

暴力破解

对于暴力破解很容易想到，因为这个数组是有时间顺序的，我们的目标也就是在满足时间顺序的要求下，找到一个最小值，找到一个最大值，二者之差就是答案。（这里的时间顺序就是最小值一定要在最大值之前）。
所以会有下面的答案。

  1.  public int maxProfit(int []prices) {
  2.         int maxprofit = 0;
  3.         for (int i = 0; i < prices.length - 1; i++) {
  4.             for (int j = i + 1; j < prices.length; j++) {
  5.                 maxprofit = Math.max(maxprofit,prices[j] - prices[i]);
  6.             }
  7.         }
  8.         return maxprofit;
  9. }

这是两个循环，其中i是遍历数组，而j是要在后续的序列中找到一个最大值来作差。比较简单，不再赘述。
时间复杂度 O(n * n)

单调栈

上述的方法又两层循环嵌套，但其实这个题目一层循环就可以实现，做如下思考，由于这个题是有时间序列的，我们可以用一个有顺序的数据结构来记录这个运行过程，如题目中的例子， 7,1,5…… 7肯定不是我们需要的，1才是。这样的话容易想到一个数据结构 “单调栈/单调队列”，所谓单调，就是栈(队列)中元素始终是单调的（比如单调递增），这样的话，为了维护单调性，破坏性的元素都要出栈（队），从而达到找到最低价和最高价的需求。

针对于 7，1，5，3，6，4 这个序列我们可以进行如下操作。

第一步，7入队，所求利润为0（当天买当天卖）
第二步，1准备入队，发现7比自己大，由于需要维护单调递增队列，就喊7出队，自己入队。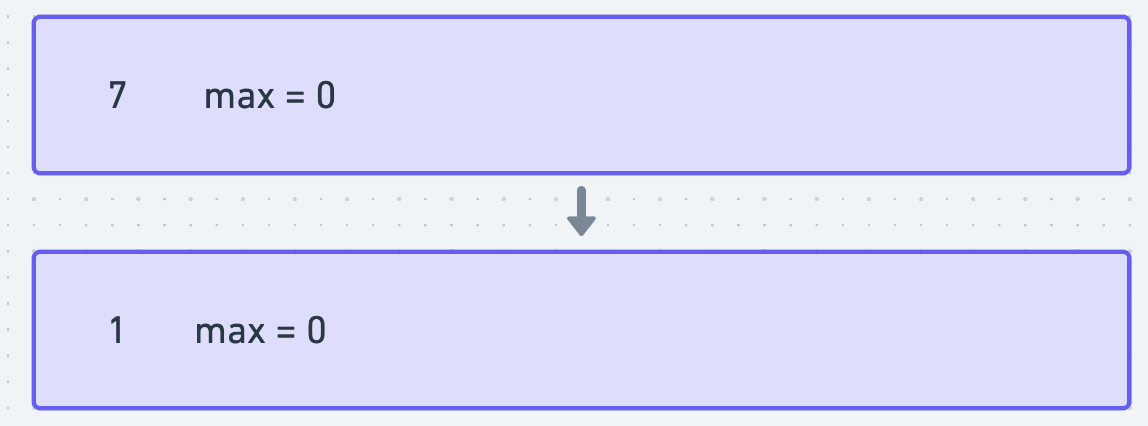
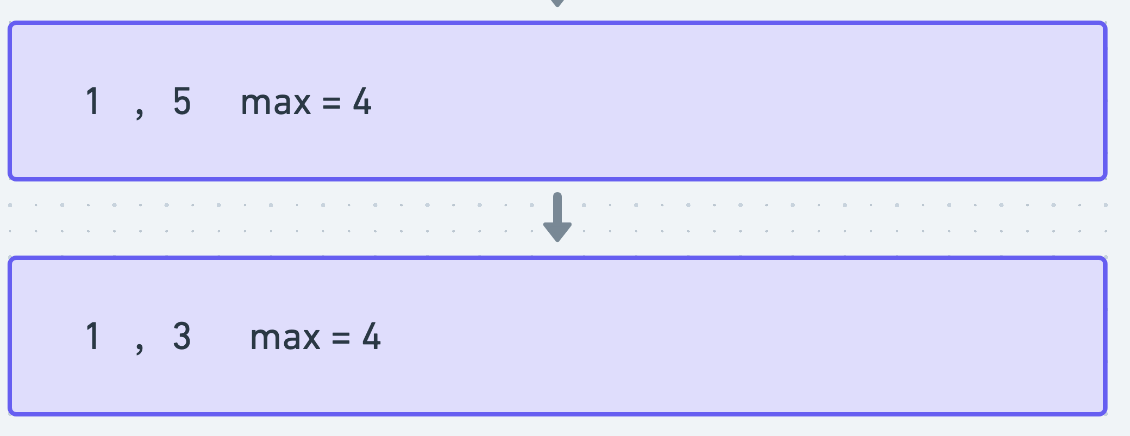
image.png
第三步，继续进行，5入队，因为自己合法递增，求得当前最大利润是4
第四步，3准备入队，发现5比自己大，就通知5出队，自己入队，但是当前最高利润已经是4了，3入队所产生的最大利润是2，不如4大，所以忽略。

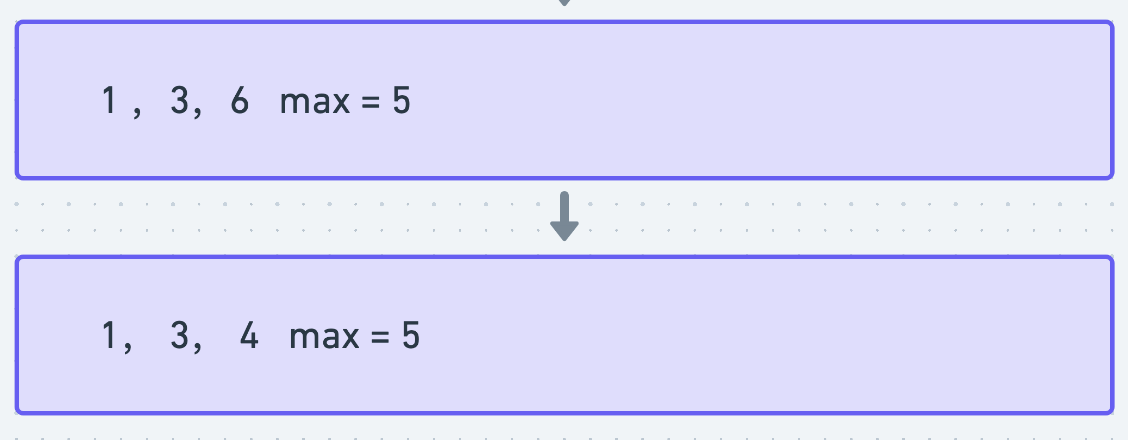
image.png

第五步，6合法入队，并贡献了自己的最大值，max = 6 - 1 = 5
第六步，4喊6出队并自己入队，最大值不如5大，所以不进行更替。

image.png

这样的话一遍循环下来，计算的最大值就是目标答案。
代码如下。

  1.  public int maxProfit(int[] prices) {
  2.         if (prices == null || prices.length == 0 || prices.length == 1) return 0;
  3.         LinkedList<Integer> stack = new LinkedList<>();
  4.         int max = 0;
  5.         for (int price : prices) {
  6.             // 这边是用来维护单调队列的
  7.             while (!stack.isEmpty() && stack.peekLast() > price) {
  8.                 stack.pollLast();
  9.             }
  10.             stack.offerLast(price);
  11.             //缓存最大值，最大值一定是当前last - 队中最小（也就是first）
  12.             max = Math.max(max, stack.peekLast() - stack.peekFirst());
  13.         }
  14.         return max;
  15.  }

时间复杂度是 O(n) 空间上有一定的投入。

On的另一种方法

上面介绍了一次遍历的一种方案，其实还有更简单的，代码如下。

  1. public int maxProfit(int[] prices) {
  2.         if(prices == null || prices.length == 0)return 0;
  3.         int n = prices[0];
  4.         int m = 0;
  5.         for (int i = 1; i < prices.length; i++) {
  6.             if (prices[i] > n) {
  7.                 m = Math.max(m, prices[i] - n);
  8.             } else {
  9.                 n = prices[i];
  10.             }
  11.         }
  12.         return m;
  13. }


简单描述上述算法就是，使用n维护整个序列的最小值（类似于单调队列的首位），使用m去不断探索最大值并替换最大值。

针对于 7，1，5，3，6，4 这个序列我们可以进行如下操作。

首先n = 7，开始遍历，当发现1的时候，确定这个比上一个n = 7 小，就更新 n = 1
然后当遍历到5的时候，就是计算最大值的时候，计算最大值为4，
遍历到3，最大值不变。
遍历到6 最大值为5。
遍历到4 最大值不变，得出答案。

假如说针对于 7，2，5，3，6，4，1，3 最小值会被依此更新为7，2，1，虽然更新了，但是我们时钟通过m来记录目标利润最大值，所以不必担心更新导致的数据异常。

动态规划

首先我们要明白一个事情，要求当天卖出股票利润最大，当然是希望前几天的利润最大，然后再计算当天的数据对利润的影响， 这样一遍遍历下来，我们就可以知道最大的利润是多少。想到这里就出来分治或者动态规划的雏形了，但是很显然这不是一个分治问题，因为 当天 和 前几天 之间存在关系，由于存在关系，我们很容易想到状态转移这个事情，所以可以用动态规划试一试。

使用动态规划一般有三个步骤：

  1. 需要确定d(i)所表示内容
  2. 根据dp(i) 和dp(i - 1)的关系得出状态转移方程
  3. 确定初始条件 dp(0)

下面使用动态规划解答这道题目。
上面说过，如果要求当天卖出股票利润最大，是希望前几天的利润最大。所以我们确定d(i)是表示当天利润，但也要考虑当天卖出对利润所造成的影响，这样当天就有两个状态 卖或者不卖，这样我们可以得出转移方程 dp[i] = max(dp[i - 1] , prices[i] - minPrice)，其中prices[i] 是当天价格，minPrice是历史最低价。
初始条件是第一天的利润，根据实际d[0] = 0,代码如下。

  1.   public int maxProfit(int[] prices) {
  2.         if (prices == null || prices.length == 0 || prices.length == 1) return 0;
  3.         int[] dp = new int[prices.length];
  4.         int minPrice = prices[0];
  5.         dp[0] = 0;
  6.         for (int i = 1; i < prices.length; i++) {
  7.             minPrice = Math.min(prices[i],minPrice);
  8.             dp[i] = Math.max(dp[i - 1], prices[i] - minPrice);
  9.         }
  10.         return dp[prices.length - 1];
  11.     }


针对于 7，1，5，3，6，4 **这个序列我们可以进行如下操作。

  1. 第一天利润为0，历史最低价7
  2. 第二天利润为 -6 （记做0），历史最低价1
  3. 第三天利润为 5 - 1 = 4 历史最低价1 ，历史利润为0 ，更新为当前的4
  4. 第四天利润为 3 - 1 = 2 历史最低价1，历史最高利润为4，保持为第三天的4。
  5. 第五天利润为 6 - 1 = 5 历史最低价1，历史最高利润为4，更新为当前的5
  6. 第六天利润为 4 - 1 = 3 历史最低价1，历史最高利润4，保持记录为第五天的5。

返回结果为第六天所保持（或者更新）的利润值。

image.png

总结

上面分别用四种方法解答了这个题目，其中单调栈和动态规划的方法在解决其他类似的问题中也很实用，建议掌握。