从最长重复子(数组/序列)看动态规划：状态转移

这题DP就完事了。

上篇文章讲到了动态规划的子问题，也顺便引出来求解过程，但是仅通过最简单的青蛙问题来讲解的，这还远远不够。恰巧本月的每日一题是动态规划专题，借此机会深入了解一下动态规划。

1. 最长重复子数组问题

给两个整数数组 A 和 B ，返回两个数组中公共的、长度最长的子数组的长度。

题目给定两个整数数组，要求返回公共最长子数组长度。如示例给的两个数组最长公共子数组是 3，2，1 。
首先我们看数据规模 1000一般暴力破解是不太可能了，所以我们不需要写遍历枚举的代码了，我们直接入正题，乍一看这道题目跟LCS很像。

LCS是最长公共子序列问题，很经典的一个动态规划问题，后面也会提到这个问题。但是与本题不同的是，LCS里是子序列并不是子串，子序列是可以不连续的。LCS算法可以用于判断两段文字的相似度，在查重方面有较多应用。

但是其实比LCS要简单一些，接下来就分析一下。
首先这个问题的名字叫做 最长 **，一般是可以采用动态规划来求解的；然后可以想到的是求解某两个长串的公共子数组，可以先求解子串的，然后一点一点扩大成最终问题，因此我们尝试用动态规划来求解。

• 确定状态
• 求解初值
• 状态转移方程
• 求解的问题是什么
• 空间优化（可选）

**
上面我又贴出来上篇给到的DP求解思路了，针对于这个问题我们首先确定状态，也就是说我们要知道 dp[i] 是代表什么意思。但是实际上我们有两个串，仅用dp[i] 并不能表示，于是将dp数组加一维，变成了dp[i][j] ,那么 dp[i][j]代表什么？我们求的是最长公共子数组，那么dp[i][j]就代表了A的子数组与B的子数组的最长公共子数组，这句话看起来绕，其实dp[i][j] 就是目标问题的一个子问题，其中 i 可以取 0 到 A.size - 1 , 而 j 可以取 0 到 B.size - 1。 有了取值范围之后我想大家都明白了，这就是在枚举各种情况，比如下面这个例子。

A: [1,2,1] B: [3,2,7]各个值的含义 dp[0][0] : 子串1 和子串3的答案 dp[0][1] : 子串1 和子串3,2的答案 dp[1][0] : 子串1,2和子串3的答案 ……

所以动态规划就是在暴力枚举。
有了这个子问题定义之后，我们就可以得出第四步 “求解的问题是什么”，即 dp[A.size - 1][B.size - 1] ，有了定义和要计算的目标之后我们要开始为这个目标努力了。（事实上本题的最终问题并不是在这个点上，后面会一步一步的纠正）

2. 填表格

因为是个二维数组，我们要求的是dp[A.size - 1][B.size - 1],** *因此我们要把这个值得到，在这里就开始体现动态规划的状态转移思想了，我们要求的这个值，一定是由其他值计算出来的，不可能凭空就出来这个值，那我们这样大费周章干嘛对吧。前面说了暴力枚举，因此我们要对二维数组中的每个值都进行计算，于是有了填表格这种说法， 填表格在动态规划问题中比较常见，也是比较有意思的一件事情。针对于题目问题，我们建立一张5 5的表格（二维数组），其中红框内的格子，我们一会要将他们填满。

对与上面的表格，我们确定了一个开始点，一个目标答案点，接下来我们从开始点行优先来遍历二维数组。这是一种最普通的遍历方式，dp的填表有各种顺序，但他始终保持一个原则，待求的点一定是需要依赖于已求得答案的点，所以当我们求某个点的时候，一定要想清楚，他所依赖的点是否已经求出来了，在应用场景中，除非有特殊要求，默认就行优先遍历即可。
根据前面的解题步骤和上一篇的青蛙问题来看，求解动态规划问题需要确定一些初始值，通常初始值是最基础的，最简单的情况。

如图所示，本题绿框之外的点都是可以直接填写的，因为他们比较简单，同时，他们也必须初始化的时候填写，因为绿框中的点是要依赖于他们的。即求解此类动态规划问题的时候，i = 0 和 j = 0（也就是绿框外的点）一般是人为推算出来，然后提供给其他点使用的。

注意，后续我都会直接以红框所表示的二维数组下标来称呼这个点, 如开始点(0,0)

我们首先看下初始化后的表。

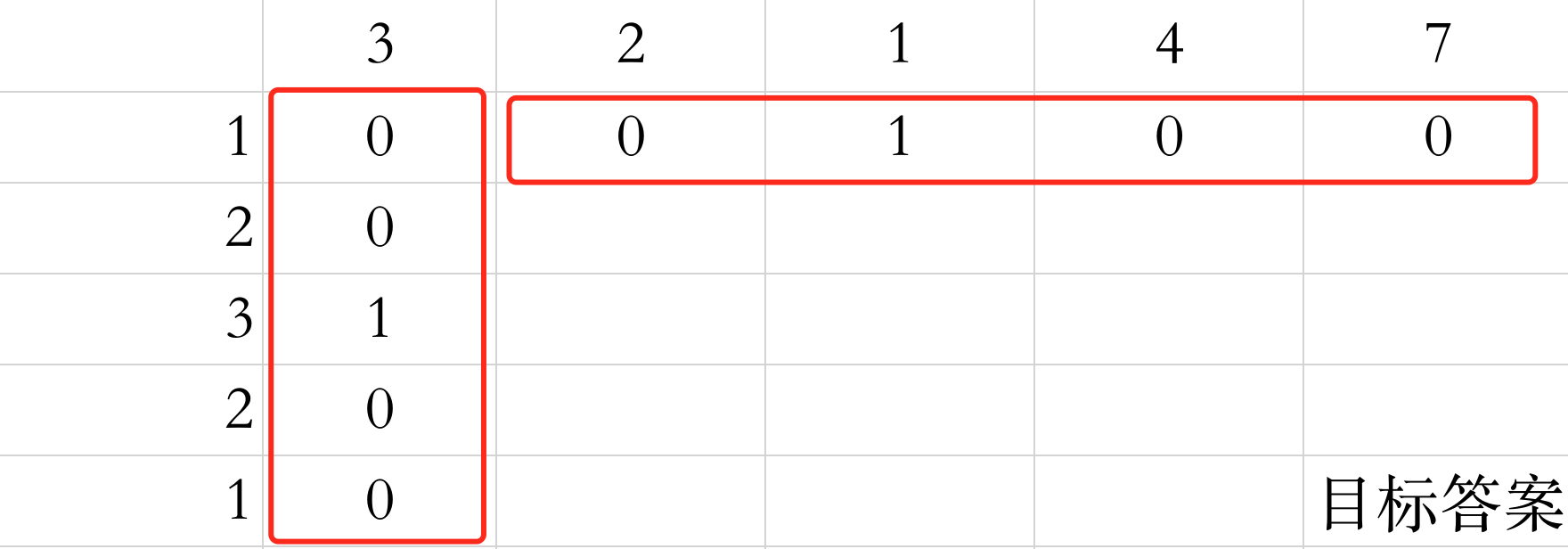
初始化是怎么填呢？我们只需要时刻牢记每个格子代表的含义即可，比如说（0，0） 代表了求 1 和 3 的最长公共子数组长度，这当然为0了。再比如说
（0，2）代表了求 1 和 3.2.1 的最长公共子数组长度，很显然最后一位相等，长度为1。
但是为什么 (0,3)(0,4) 还有一些点他的值跟想象中的值不一样呢？其实这也是LCS与本题的区别了，这个原因我还要稍后再说。那么很明显, 如果这样写最后读表格我会读到错误值啊，比如说表格是1 * 5的，我求 （0,4），那肯定不是正确答案。因此我们需要用一个缓存变量来保存，此时就又出现了问题，既然表格上的值出现了不准确性，那吗目标答案肯定也是不准确的，所以我们也不能用了。这是很重要的一点，由于这个题的特殊性，我们之前所做的假设都需要纠正了，但虽然目标答案的假设不正确了，这也不能否认我们的遍历顺序和遍历的起点和终点。
接下来就是重头戏了，真正的进入了动态规划的状态转移的阶段了。此时为了完成状态转移，我们需要确定一个父问题和子问题的关系。

观察绿框里的点，对应的横向的值为2，纵向也为2，因此他们为最长公共子数组长度 ”贡献了1个单位“ ，他们俩所贡献的，加上数组中排在他们前面的元素所贡献的值，就是当前子问题的值，也就是这个格子的值。于是我们可以针对剩下的4 * 4格子得出下面的状态转移方程。

首先第一行我们已经说过了，如果他们相等，那么当前格子就等于 1 + 去掉他们的之前子数组所贡献的值，那么如果他们不相等，这个0又从何说起呢？
还记得我们之前留下的疑问么，为什么那些位置不能写正确值，只能写0？其实是因为题目所要求的的连续子数组所影响的，想象这样一个场景。
某个位置继承了他前面的点所贡献的值，但实际上他并自己并没有贡献，也就是说此时的 A[i] != B[j] , 从他这里数组的连续性已经断掉了，那么后面的点，比如他右下角这个点可能需要继承他的值的，此时继承来的答案是正确的么？并不是，因为已经不连续了。如表格中，如说我给(0,3)这个点继承了1这个数值，假设(仅仅是假设) (1,4) 这个点横向和纵向两数恰好相等并准备贡献 1个单位，那么按照转移方程它取左上角的值的时候并不知道左上角的点对应的情形已经不连续了,因此会得到一个错误答案。这也是连续子数组/子串与连续子序列的区别。
因此按照这个方程，我们填写完的表格如下。

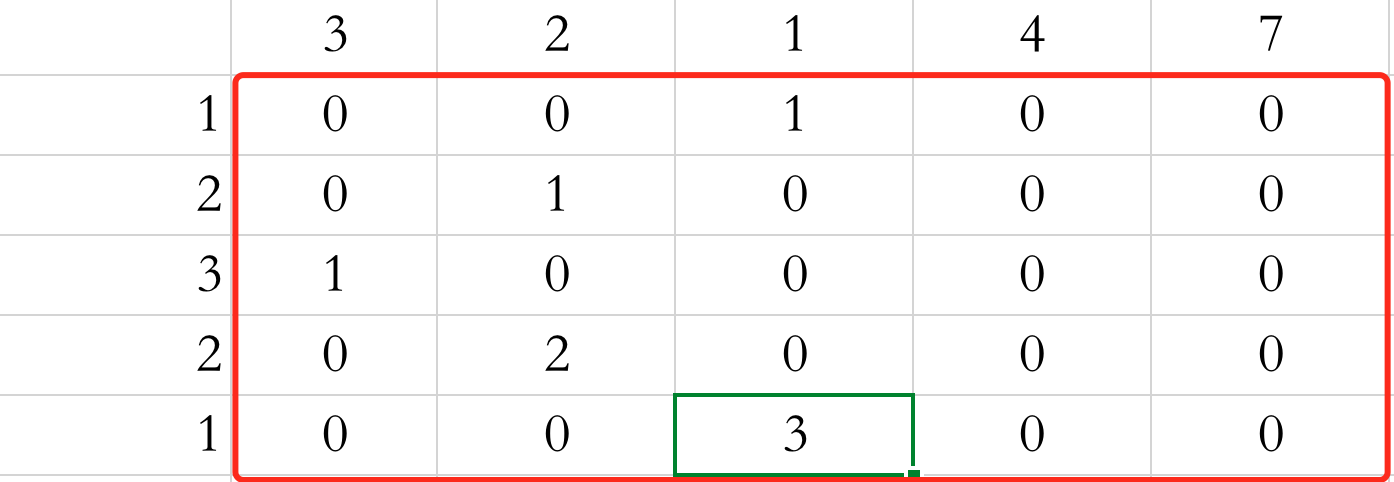
还记得我们有一个临时变量存储最大值么？当我们边填边记的时候，绿框中的3这个值就被记录下来了，最终我们返回的答案也是这个，可以看到，这个最终答案并不是在最后一个位置，这也是这个题目的特殊之处，建议多回味一下上面说的连续所引发的”锅“

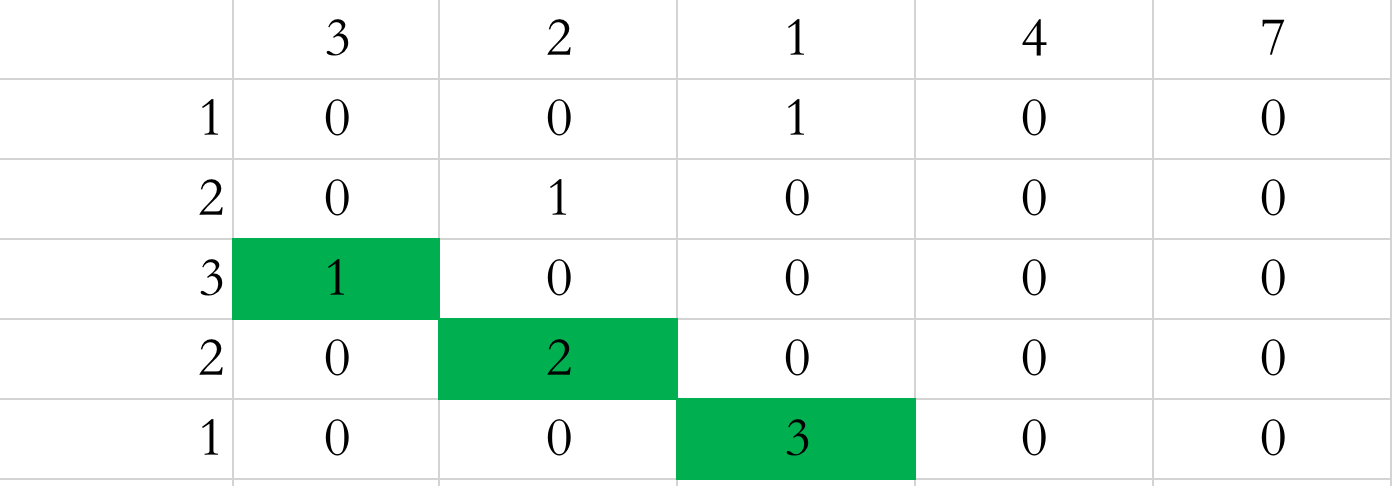
再就是，我们通过最终的表可以发现，我们所求的连续子数组总是一个斜对角线的形式，这也是为什么某个点要跟左上角点联系起来的原因。

3. 编码

我们花费了很多时间来分析如何填表格，接下来就是编码了。其实有了前面的铺垫，这个编码过程简直是轻而易举，因为上面的表格就是二维数组嘛，所以建立数组，遍历填写初始值和其他值，然后记录最大值即可。

//lang: kotlin
fun findLength(A: IntArray, B: IntArray): Int {
    //👇这里，建立二维数组 
    val dp = Array<Array<Int>>(A.size) { Array(B.size) { 0 } }
    var ans = 0
    //👇这里，开始遍历填写二维数组 
    for (i in dp.indices) {
        for (j in dp[0].indices) {
            //👇，我们说相等即转移，不相等就为0，这同样适用于初始值的填写
            if (A[i] == B[j]) {
                //👇，初始值所秉承的原则是相等就是1。
                if (i == 0 || j == 0) {
                    dp[i][j] = 1
                } else {
                    //👇，不多说了。
                    dp[i][j] = dp[i - 1][j - 1] + 1
                }
            } else {
                //👇，这个也不多说了
                dp[i][j] = 0
            }
            ans = Math.max(ans, dp[i][j])
        }
    }
    return ans
}

其中我们直接在最外层判断了两值是否相等，相等再分为初始值和转移值，而不等就直接pass掉，填入我们之前一直强调的0。
此外，在填写初始值的时候，我们遇到相等的总是赋值为1，因为初始值没有左上角贡献（左上角越界了~），所以只需要填写自己贡献的一个单位即可！

在熟悉了上面的转移过程，或者说是填表套路之后，我们可以来看一下LCS是如何实现的，LCS是一个经典的问题，很多算法题都可以通过它变种而来，有了上面的经验我们再看LCS就显得异常轻松了。

4. LCS问题

这道题目在leetcode也有：最长公共子序列，前面我们已经提到过了，公共子序列和公共子数组/子串的区别是是否连续，那么按照我们的分析，这道题目套路也是一样的，定义表格，找到转移方程，填写表格。而且上面已经说过因为不连续导致的问题，在这个题目中统统都没有。所以我们可以直接上手。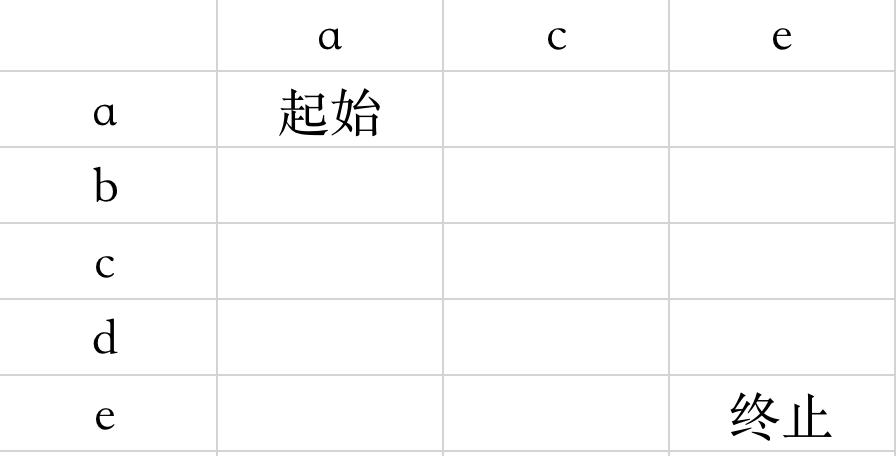

依然按照行优先的填表方式，确定起始点为(0,0)，终止点为(4,2)。初始化值的过程我们在之前已经说过了，如果相等就贡献一个单位，所以我们将行和列都初始化。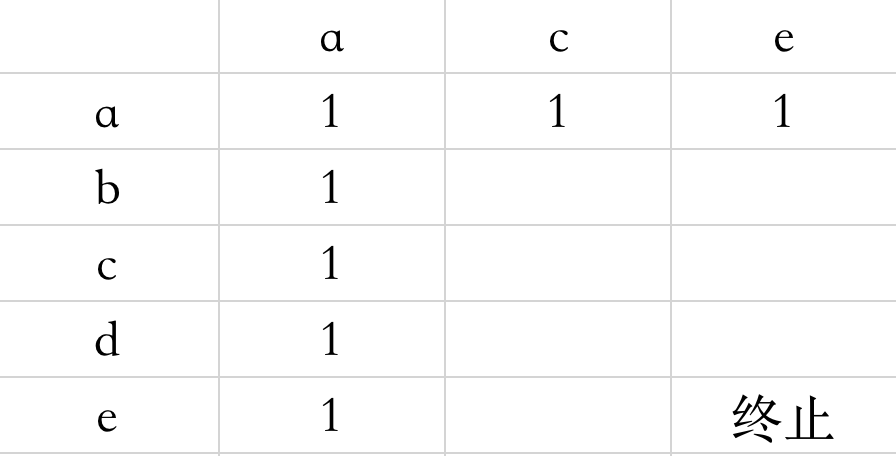

接下来就是求转移方程了，也是整个题目的重点，我们在最长公共子数组的题目中利用的是其左上角的值，而在这个题目中，我们自然也可以继承这一特性。

也就是当最后一位是相等的情况下，就是他们的子串的值，加上相等这一位贡献的1,那么如果他们不相等呢？我们知道由于子序列未要求一定连续，所以当前所求位置的值可以继承他的子问题的值，那么他的子问题是什么？
举例说明，如我要求 (1,1)位置的值，也就是求 a,b 与 a,c的LCS，它的子问题可以是 a,b 与 a ，也可以是 a 与 a,c 或者是 a 与 a ，那么我们所求的状态转移，所求的“最长“，就是从这几个子问题中选择一个最值。

这样我们的转移方程就有了。

实际上，对于dp[i-1][j-1]这个值，一定是小于其他两个子问题的值的，因为他所计算的顺序是优先与其他两个子问题的，我们也能看出来这个转移方程中，没有减法，所以按照行顺序只能是只增不减(或者保持)的，因此，我们也可以在方程中省略这一部分。

我们继续用刚才的代码来改写。

fun longestCommonSubsequence(text1: String, text2: String): Int {
    val dp = Array<Array<Int>>(text1.length) { Array(text2.length) { 0 } }
    for (i in dp.indices) {
        for (j in dp[0].indices) {
            dp[i][j] = when {
                i == 0 && j == 0 -> if (text1[i] == text2[j]) 1 else 0
                i == 0 -> if (text1[i] == text2[j]) 1 else dp[i][j - 1]
                j == 0 -> if (text1[i] == text2[j]) 1 else dp[i - 1][j]
                else -> if (text1[i] == text2[j]) dp[i - 1][j - 1] + 1 else Math.max(dp[i - 1][j], dp[i][j - 1])
            }
        }
    }
    return dp[dp.size - 1][dp[0].size - 1]
}

这种写法也是需要额外处理边界值的，这里用的是kotlin的when语法，相当于Java的switch，然后对每一个分支，判断是否最后一位相等，按照我们之前说过的相等和不等的转移方程计算即可。只不过需要注意的是，横向和纵向的值最小为0，最大为1，只要横向出现了一个1，那么后面将全部是1，同理只要纵向出现了一个1，后面个将全部是1。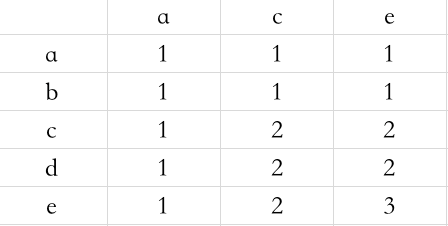

这就是我们最后的表格。

5. 总结

上面给了两个例题，他们之间有联系也有不同，针对于不同的点，我们对转移方程进行了细微调整。转移方程是动态规划中重要的一环，掌握一些经典的题目的转移方法有助于举一反三，来破解更多的题目。同事在本文中，给到了借助于二维数组所实现的动态规划的解决方法（填表格），主要就是确定起始点和终止点，口算或者推断初始值，然后根据初始值，并按照一定的方向进行状态转移。，.
本文就到这里啦，在后面的文章中，将会讨论”转移方向”和”空间优化”等问题。