这题DP就完事了。
提到动态规划(后文简称dp),脑子里除了一个字“难”就没别的了,实际上基础的dp看起来又不复杂,核心的地方就是初始值和转移方程。不过正是因为转移方程搞得大家焦头烂额,而且刷了很多题还是看不能找到转移方程有什么规律。才疏学浅,我也总结不出什么高深的内容,所以我从经典题目入手来丰富这套知识体系。
1. 说在解题之前的内容
一方面,dp经常用来求解最优解问题,比如最长公共子序列(LCS),最小编辑距离等,也可以求解类似于凑硬币,青蛙跳台阶等统计方案的问题。所以也不见得就必须是要求解最优问题。
另一方面,dp解题过程中,经常提到子问题,也就是将最终的大问题分解成一个个的小问题,再分别求解小问题以计算大问题。但实际上大部分问题都能大化小,如果单纯的讲大化小还不如说这是一个分治思想(很显然,dp可以作为分治的子集)。实际上dp的关键在于它可以消除求解过程中的重叠子问题,正是因为消除了重叠子问题,dp的优势才显现出来。
提到重叠子问题,我们就来看下青蛙类问题。
2. 从青蛙问题理解dp
很有意思的一个题目,同样也很经典,有不同的解法。青蛙跳台阶问题
关注这道题目让我们求的内容,方案总数。一般求解这种方案总数的问题都会具有递推性质。按照递推思路来看可以得出下面的结论。
其中f(x)代表总共有x个台阶的时候跳跃方案总数
上面所表示的式子的含义是: 如果一共有3个台阶,方案总数就是 想要跳到第一个台阶上的方案总数 加上 想要跳到第二个台阶上的总数,因为如果我当前站在第一个台阶上,那么我再一下跳2级就可以完成目标,同理如果我当前在第二个台阶,我再跳1级就可以。
扩大问题规模。
如果当前有n个台阶,同理因为每次最多只能跳1级或者2级,那么一定有
到这里,其实我们发现递推公式被我们写出来了。然后敏感的童鞋就会看到这其实是一个斐波那契递推式。通常我们会用递归来求解斐波那契问题。
public static int f(int n) {if (n <= 1) return 1;if (n == 2) return 2;return f(n - 1) + f(n - 2);}
斐波那契的递归写法如上,我们按照题意对初始值做了调整,这样这个题就被解决了。但这是最佳答案吗?必然不是,学过斐波那契的童鞋肯定知道重复子问题这个事情。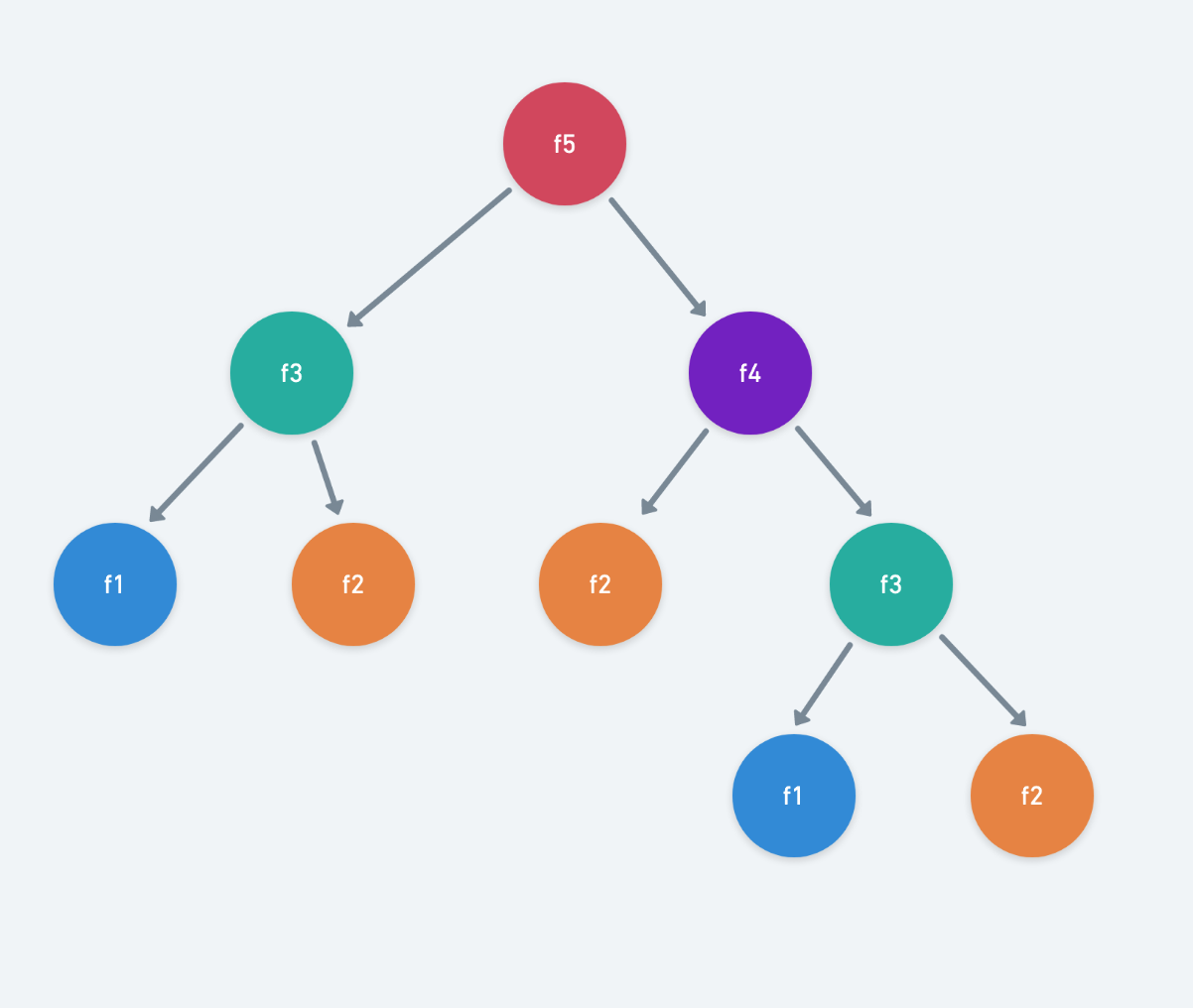
如上图所示,求F5的时候,出现了很多重复的子问题,比如F2重复了3次,F1重复了1次,F3重复了2次 我都已经用相同颜色标注了出来,这是一棵相对简单的递归树,可以想象当数据规模特别大的时候,不少子问题将会被重复n多次。按照二叉树的特点,一个节点至多拥有两个孩子,不断分裂的节点数将达到规模,按照每个子问题的求解时间为
那么复杂度将达到
指数级别呈爆炸式增长,性能可想而知。
当然如何避免重复的计算子问题也很显然,假如说我当前已经计算了F3的值,如果下次我要调用F3,直接取值就好了。要存储这些信息当然是选择HashMap了。
static HashMap<Integer, Integer> map = new HashMap<>();public static int f(int n) {if (n <= 1) return 1;if (n == 2) return 2;if (map.containsKey(n)) return map.get(n);int result = f(n - 1) + f(n - 2);map.put(n, result);return result;}
上面的代码经过了优化,会将某次计算的值存到hashmap中,如果下次又需要计算这个值,就可以直接取到。
如上图所示,重叠部分都不需要计算,省略了大部分额外操作。这种记忆化的操作叫做备忘录,通过这种方法的剪枝一棵复杂递归树就被简化成了不存在冗余的递归调用。
这时候我们再看,在我们求解的过程中,每个子问题都仅被求解了一次(边界条件我这里没有备忘,产生影响较小),也就是说求规模为N的问题,复杂度仅为,这个优化相比上面的普通版本确实好了很多,在这里使用到了HashMap,是典型的空间换时间的做法。
上面的内容都是很基础的递归知识,说他们就是为了引出dp的骚操作。
小盆友一脸问号的问我,既然递归这么耗时间还要什么备忘录这么“高大上”的东西来优化我们为什么不用迭代呢?
有道理,我们上面看到的递归写法是 自顶向下 的,也就是说我要求F10,要先去求F9和F8,然后返回,此为递归。而使用迭代,我们必须先求出最小子问题,然后累加组成下一个子问题。这就是斐波那契的迭代写法。
public int f(int n) {int[] dp = new int[n + 1];dp[1] = 1;dp[2] = 2;for (int i = 3; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
是不是很简单,首先创建了一个数组,然后对初始的方案数进行了填写,最后迭代填写剩下的数。这种形式是 自底向上 的。可以看到,这里我已经将备忘录换成了数组,并起名为dp了,实际上这就是我们的dp版本。
3. dp的求解思路
上文我们通过青蛙问题简单的理解了一下dp,其实发挥核心作用的就是斐波那契数列的公式,在dp问题中,我们称之为 状态转移方程,通常我们求解dp问题就是奔着求解状态转移方程去的,而且状态转移方程也通常分为初始条件和转移部分。如青蛙问题中,状态转移方程如下所示。
现在我们看这个方程就熟悉的很了,分为3种情况,上面的代码中也已经体现出来了。由此我们也可以总结出大部分动态规划题解或者技巧文章中经常给到的求解步骤:
- 确定状态
- 求解初值
- 状态转移方程
- 求解的问题是什么
- 空间优化(可选)
但,恕我直言。这通常只有一个指引作用,就像你背了一个作文模板并不知道怎么用一样。因为题目是在变化的,而动态规划又不是跟BFS,DFS,二分查找等问题一样模板甚至都固定的,他只能给你一个引导,让你明确是有这么几步要干,通常我第一步就卡在那里,但不要为此恐惧DP问题,掌握一些经典的题目,会帮我我们更快的举一反三和理解深层次的DP。在青蛙这个问题中,状态就是,而我们之前也已经讨论过
就是代表台阶数为i的时候方案总数,而初值和转移方程上面都已经说过了,对于求解的问题,可以简单理解为到何时终止,取什么值即可。
最后一步我给了一个可选的空间优化,这个好理解,仔细看最终版的动态规划代码,发现在迭代的过程中,始终只有 和
这两个数据在工作,所以我们可以省略DP数组,将代码变成如下的样子。
public int numWays(int n) {int a = 1, b = 2, temp;if (n == 0 || n == 1) return a;if (n == 2) return b;temp = a + b;for (int i = 3; i < n; i++) {a = b;b = temp;temp = a + b;}return temp;}
这段代码也好理解,不断更新a,b和temp的值,由temp计算新值,而a和b就分别代表了 和
这两种情况。
通常动态规划的题目在可以进行如上的一些空间优化,DP数组也不是必须要有的,掌握这样的小技巧,空间复杂度可以降低一个数量级。
4. 中场休息
上面通过一个青蛙问题引出了dp,我们经历了从递归 -> 备忘录递归 -> DP -> 空间优化后的DP,层层递进解决了一个dp的问题,但这其实离真实的dp还差的多,我们上面说到dp主要是用于求最优解,而对于这种求解方案数的问题我遇到的还是比较少的(至少比求解最优解的题目少吧)。
下面会给一个青蛙题的变形。
5. 青蛙题的变形
接下来我们看一道题目,面试题46. 把数字翻译成字符串。
这道题是一道方案总数的题目,而且给定的num范围很大,暴力找每一个凑法肯定是不现实的。但如果我们这么想,求解一个字符串的翻译方法不就是求解他的子串的翻译方法么?如求解12258这个串的方案就是求解1225** 与 122 的解决方案 ,因为12258 就是1225 的方案数加上 122的方案数(当58这个数是能组成合法的字母的时候),这就跟青蛙题目有点像了,我们说青蛙一次只能跳一个或者两个台阶,这个题目一次只能选一个数字或者两个数字(两个数字可以组成L-Z), 不同的是,我们要判断这两个数字是否是 <= 25 **的,因为只有这样的数字是可以使用的。
我们直接写优化过的递归写法,下面是我做题的时候使用kotlin写的代码,不过语言都是相通的,不妨碍理解代码。我们看一下注释。
//创建一个HashMap备忘录val map = HashMap<String, Int>()//主函数递归开始,采用了int转string的形式方便后面取位fun translateNum(num: Int): Int {return count(num.toString());}fun count(str: String): Int {//特殊情况if (str.isEmpty()) return 1if (str.length == 1) return 1//对于给定的字符串var a = 0var b = 0//进行递归,并对不合法的情况进行剪枝if (str.length >= 2) {//这里的不合法主要分为两种,一种是上面提到过的 <=25 另一种是如 05 这样以0开头的也不能被转换val curStr = str.substring(str.length - 2, str.length)if (!curStr.startsWith("0") && curStr.toInt() in 0..25) {//备忘录,如果取到,那么最好,如果取不到默认就去计算,计算完成后添加到map中a = map.getOrDefault(str.substring(0, str.length - 2), count(str.substring(0, str.length - 2)))map[str.substring(0, str.length - 2)] = a}}if (str.isNotEmpty()) {//这里同样是递归,只不过我们不用额外处理不合法的情况,因为一位数总是认为合法的。b = map.getOrDefault(str.substring(0, str.length - 1), count(str.substring(0, str.length - 1)))map[str.substring(0, str.length - 1)] = b}return a + b}
刚才贴代码的时候发现我备忘录写了结果没用,但是其实还是过了的,证明其实普通不备忘的递归也能过,不过毕竟是指数级别的,建议有类似问题求解的时候都要带上备忘录及剪枝。上面已经提到过了,代码其实跟青蛙是一样的,对与终止条件或者是初始条件就是字符串为空的情况和字符串为1的情况总返回1,其他情况就正常递归,然后在减去2个数字的情况中做一些合理的剪枝以保证正确性即可。
所以说这个题目看起来很高大上,其实就是一个青蛙题。那么既然是青蛙题,我们完全可以用动态规划的思路来求解。按照之前所给到的5步计算方法来看,首先确定子问题(也就是状态)为某个子串可以转出的方案数,然后是求解初值,初值就是如果数字串为1的时候有几种,为2的时候会有几种,接下来求解转移方程,这个方程不多说了就是青蛙的方程,但需要注意对不合理的状态进行剪枝。最后是求解问题 ,同青蛙题,这题没有套路,最终结果就是dp数组中最后一个值。
fun translateNum(num: Int): Int {val str = num.toString()if (str.isEmpty()) return 0if (str.length == 1) return 1//1. 创建dp数组val dp = IntArray(str.length)//2. 对dp数组中赋初值dp[0] = 1val normal = str.substring(0, 2)if (normal.length == 2) {dp[1] = if (!normal.startsWith("0") && normal.toInt() in 0..25) 2 else 1}//3. 迭代剩下部分,并计算更新的值for (i in 2 until dp.size) {val cur = str.substring(i - 1, i + 1)dp[i] = dp[i - 1] + (if (!cur.startsWith("0") && cur.toInt() in 0..25) dp[i - 2] else 0)}return dp[dp.size - 1]}
相比之下动态规划的代码就简洁了许多,这个算法时间复杂度是,空间也是
,那么有没有希望进行第五步“空间优化”呢,答案是肯定的,其实还是说我们根本用不到dp数组,只需要3个变量推进就可以了。篇幅问题,优化的任务就交给你了哦。
6.总结及提升
上面通过一个简单的例子介绍了动态规划,但动态规划的水远远比这深,只能一点点积累了。最后从几个方面来总结一下吧。
动态规划靠什么来高效工作?
前文提到过,动态规划的求解思路是大化小,但是他在大化小的基础上消灭了重叠子问题,记录了子问题状态,本质上动态规划也是一种暴力的遍历解法,但正因为它无需走重复的路,所以达到了高效的结果。
什么样子的题目适合用动态规划?
动态规划的题目越来越受到青睐,出现的越来越频繁。但通常只适合于求解最优子结构,方案总数,或者有一种变形的问法,“某件事可不可行”。但有一种求解路径的题目,一般不会用DP来做。因为大部分情况下,DP都不会保存路径。
怎么学习动态规划?
这一点我没有什么说的,因为我也不会。但是不得不双标一把,上面提到的动态规划5步求解过程还是要熟记于心。此外可以尝试用递归去解决问题,然后逆转思路引出动态规划。 不要恐惧状态转移方程,这个听起来高大上的名字,其实就是数学上的数列问题或者找规律问题。而且通常情况下,求方案总数的题目是直接进行基础运算,最优结构问题的规律中含有max和min的操作。
此外基础的DP还会包括二维,二维的方向,最优的选择等等等一系列问题,后面会慢慢引入。最后贴一个与青蛙一模一样的题目。70. 爬楼梯 可以在不参考青蛙的代码的情况下练手一下。
拜拜,下次见。

