大纲
网络统计量
度与度分布
节点的度
节点 的度
定义为与该点连接的边数。
所有节点度的平均值称为网络的平均度
度分布
#card=math&code=P%28k%29&height=20&width=34) 表示度为
的节点在整个网络中所占的比例,一般用直方图表示度分布。
规则网络
所有的节点都有相同的度,度分布集中在一个尖峰,为Delta分布
完全随机网络/均匀网络
当 时,呈指数下降,Poisson分布
%3D%5Cfrac%7B%5Clambda%5Ek%7D%7Bk!%7D%5Cmathrm%7Be%7D%5E%7B-k%7D%0A#card=math&code=P%28k%29%3D%5Cfrac%7B%5Clambda%5Ek%7D%7Bk%21%7D%5Cmathrm%7Be%7D%5E%7B-k%7D%0A&height=42&width=105)
无标度网络
幂律分布/无标度分布:%3DbF(1)#card=math&code=F%28ax%29%3DbF%281%29&height=20&width=107)
%20%5Cpropto%20k%5E%7B-%5Cgamma%7D%0A#card=math&code=P%5Cleft%28%20k%20%5Cright%29%20%5Cpropto%20k%5E%7B-%5Cgamma%7D%0A&height=21&width=86)
累积度分布
度不小于 的节点的概率分布:
%0A#card=math&code=Pk%3D%5Csum%7Bi%3Dk%7D%5E%7B%5Cinfty%7DP%28i%29%0A&height=49&width=99)
幂律分布:
%7D%0A#card=math&code=Pk%5Cpropto%20%5Csum%7Bi%3Dk%7D%5E%7B%5Cinfty%7D%7Bi%5E%7B-%5Cgamma%7D%7D%5Cpropto%20k%5E%7B-%5Cleft%28%20%5Cgamma%20-1%20%5Cright%29%7D%0A&height=49&width=164)
指数分布:
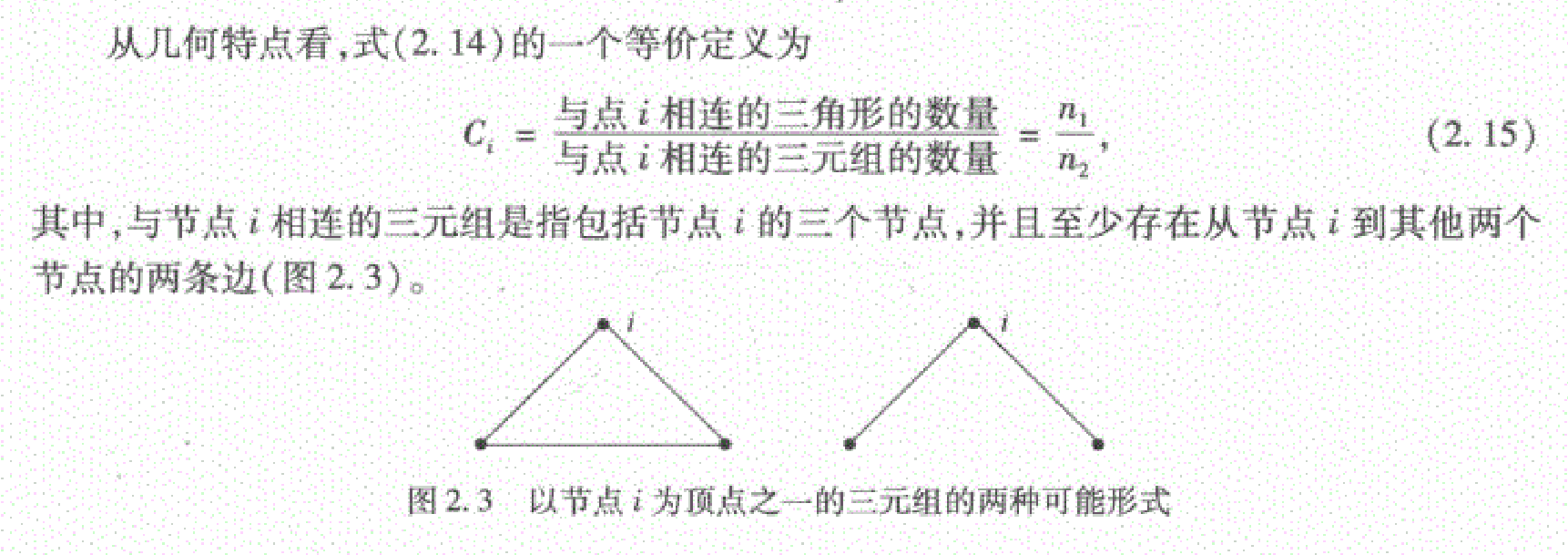
聚类系数
:节点
的
个邻居之间存在的边数
:节点
的
个邻居之间最多存在的边数
网络模型
规则网络
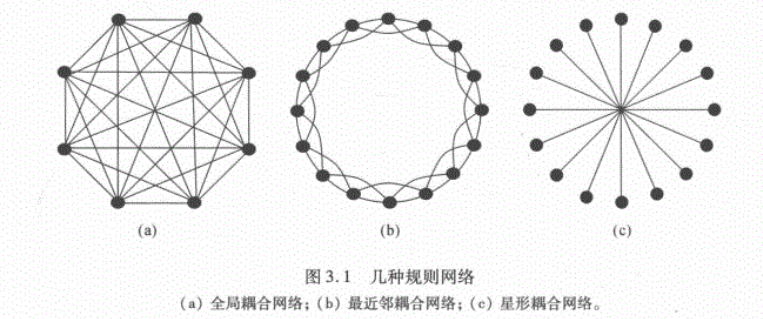
平移对称性:每个节点的度和聚类系数相同
全局耦合网络
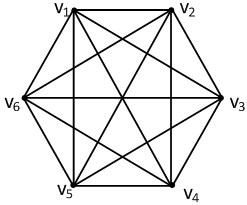
每个节点之间都有边相连:
- 各节点的度均为N-1,因此度分布为单尖峰,可以表示为Delta函数
.
- 每个节点
的集聚系数均为
,故整个网络的集聚系数为 C=1。
- 从任意一个节点到另外一个节点的最短路径长度都为1,故整个网络的平均距离为L=1。
在具有相同节点数的所有网络中,全局耦合网络具有最小的平均距离和最大的集聚系数。
该模型作为实际网络模型的局限性很明显:全局耦合网络是最稠密的网络,然而大多数大型实际网络都是很稀疏的,它们边的数目一般至多是而不是
最近邻耦合网络
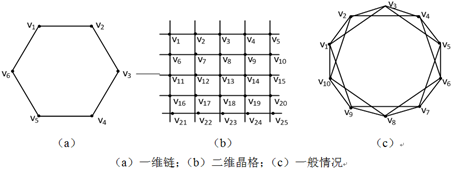
每个节点只与周围节点相连。 个点围成一个环,每个节点只与左右
个邻居节点相连
星性耦合网络
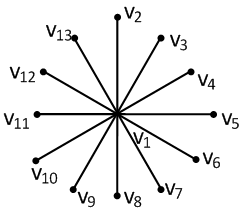
只有一个中心点,与其余点相连
随机网络
ER 模型
个节点最多存在
%2F2#card=math&code=N%28N-1%29%2F2&height=20&width=88)条边,随机选出
条边
二项式模型
性质
- Possion度分布
- 平均距离短
- 聚类系数小
%20%5Capprox%20pN%0A#card=math&code=%5Cleft%3C%20k%20%5Cright%3E%20%3Dp%5Cleft%28%20N-1%20%5Cright%29%20%5Capprox%20pN%0A&height=20&width=158)
%20%3DC%7BN-1%7D%5E%7Bk%7Dp%5Ek%5Cleft(%201-p%20%5Cright)%20%5E%7BN-k-1%7D%5Capprox%20%5Cfrac%7B%0A%5Cleft%3C%20k%20%5Cright%3E%20%5Ek%5Ctext%7Be%7D%5E%7B-%5Cleft%3C%20k%20%5Cright%3E%7D%7D%7Bk!%7D%0A#card=math&code=P%5Cleft%28%20k%20%5Cright%29%20%3DC%7BN-1%7D%5E%7Bk%7Dp%5Ek%5Cleft%28%201-p%20%5Cright%29%20%5E%7BN-k-1%7D%5Capprox%20%5Cfrac%7B%0A%5Cleft%3C%20k%20%5Cright%3E%20%5Ek%5Ctext%7Be%7D%5E%7B-%5Cleft%3C%20k%20%5Cright%3E%7D%7D%7Bk%21%7D%0A&height=45&width=300)
大规模的稀疏ER随机网络没有聚类特性.
规则网络的普遍特征是集聚系数大且平均距离长,
而随机网络的特征是集聚系数低且平均距离小。
小世界网络
尽管一些网络系统有很大的尺寸,但任意两个节点之间却存在一个相对小的距离。
- 短距离
- 高聚类系数
WS小世界模型
- 生成一个
个点的最近领耦合网络,每个节点只与左右
个邻居节点相连
- 每条边以概率
随机重新连接:一端点不变,令一端点随机选取连接
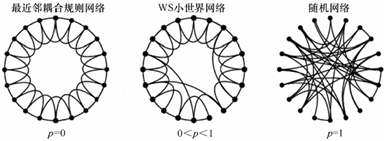
对应完全规则网络
对应完全随机网络
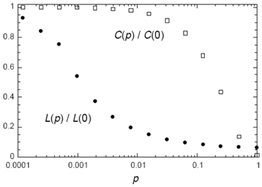
集聚系数 C(p) 和平均距离L(p)
一方面,只要几条边的随机重连就足以减小网络的平均距离;
另一方面,几条随机重连的边并不足以改变网络的局部集聚特性。
这类既具有较短的平均距离又具有较高的集聚系数的网络就是典型的小世界网络。
网络性质对比
网络增长过程
最近邻耦合网络
N=20
K=2,4,8,20
clc, clear, hold onaxis equalN=20; K=2; %N为网络节点总数,K为邻域节点个数t=0:2*pi/N:2*pi-2*pi/N; %生成最近邻耦合网络各节点坐标的参数方程的角度x=100*sin(t); y=100*cos(t);plot(x,y,'ro','MarkerEdgeColor','g','MarkerFaceColor','r','markersize',6);A=zeros(N); %邻接矩阵初始化for i=1:N %该层循环构造最近邻K耦合网络的邻接矩阵for j=i+1:i+K/2jj=(j<=N)*j+(j>N)*mod(j,N); %如果j超过了N,要取除以N的余数A(i,jj)=1; A(jj,i)=1;endendfor i=1:N-1for j=i+1:Nif A(i,j)~=0plot([x(i),x(j)],[y(i),y(j)],'linewidth',1.2);endendend
随机网络
N=20
p=0.02,0.1,0.5,1
clc, clear, hold onaxis equalN=20; p=0.99; %N为网络节点总数,p为连接概率t=0:2*pi/N:2*pi-2*pi/N;x=100*sin(t); y=100*cos(t);plot(x,y,'ro','MarkerEdgeColor','g','MarkerFaceColor','r','markersize',6);A=zeros(N); %邻接矩阵初始化z=rand(N,N);for i=1:N-1for j=i+1:Nif(z(i,j)<=p)A(i,j)=1; A(j,i)=1;plot([x(i),x(j)],[y(i),y(j)],'linewidth',1.2);endendend
小世界网络
N=20
K=8
p=0,0.2,0.5,1
clc, clear, hold onaxis equalN=20; K=6; p=1; %N为网络节点总数,K为邻域节点个数,p为重连概率t=0:2*pi/N:2*pi-2*pi/N; %生成最近邻耦合网络各节点坐标的参数方程的角度x=100*sin(t); y=100*cos(t);plot(x,y,'ro','MarkerEdgeColor','g','MarkerFaceColor','r','markersize',6);A=zeros(N); %邻接矩阵初始化for i=1:N %该层循环构造最近邻K耦合网络的邻接矩阵for j=i+1:i+K/2jj=(j<=N)*j+(j>N)*mod(j,N); %如果j超过了N,要取除以N的余数A(i,jj)=1; A(jj,i)=1;endendfor i= 1:N %该层循环进行随机重连for j=i+1:i+K/2jj=(j<=N)*j+(j>N)*mod(j,N);ChangeV=randi([1,N]); %产生随机整数,为可能重连的另外一个节点if rand<=p & A(i,ChangeV)==0 & i~=ChangeV %重连的条件A(i,jj) = 0; A(jj,i) = 0; %删除原边A(i,ChangeV)=1; A(ChangeV,i)=1; %重连新边endendendfor i=1:N-1for j=i+1:Nif A(i,j)~=0plot([x(i),x(j)],[y(i),y(j)],'linewidth',1.2);endendend
对应参数对比
初始化参数:
最近耦合网络N=20K=8小世界网络N=20K=8p=0.5随机网络N=20p=0.42
**
| None | N | M | d | L | C |
|---|---|---|---|---|---|
| 最近耦合网络 | 20 | 80 | 8 | 1.7368 | 0.6429 |
| 随机网络 | 20 | 81 | 8.1 | 1.5842 | 0.3702 |
| 小世界网络 | 20 | 80 | 8 | 1.6000 | 0.5028 |
function [D,L,dist]=myAPL(a);%计算网络直径D,平均路径长度L,和所有节点对之间的最短距离dist;输入参数a为网络的邻接矩阵a=tril(a); %截取邻接矩阵的下三角部分,满足Matlab工具箱的要求a=sparse(a); %转换成稀疏矩阵,Matlab工具箱的要求dist=graphallshortestpaths(a,'directed',false);D=max(max(dist)); %计算网络直径Ldist=tril(dist); %提取最短距离矩阵的下三角部分he=sum(nonzeros(Ldist)); %求所有边的和n=length(a); %求节点个数L=he/nchoosek(n,2); %求平均路径长度,这里使用Matlab求组合数命令
function [TC,c]=mycluster(a);%输出参数TC是整个网络的聚类系数,c为各个节点的聚类系数,输入参数是邻接矩阵n=length(a);for i=1:nm=find(a(i,:)); %找第i行非零元的地址ta=a(m,m); %提取节点vi的所有邻居节点所构成的邻接矩阵Lta=tril(ta); %提取邻居节点所构成邻接矩阵的下三角元素if length(m)==0 | length(m)==1c(i)=0; %孤立节点或只有1个邻居的节点的聚类系数定义为0elsec(i)=sum(sum(Lta))/nchoosek(length(m),2); %求节点vi的聚类系数endendTC=mean(c); %求整个网络的聚类系数
function dp=mydegree(a,s);%返回值dp是度的频数分布表,它的第一行是度的取值,第二行是对应度的频数%输入参数a为邻接矩阵N=length(a); %计算节点的个数deg=sum(a); %求各节点的度degrange=minmax(deg); %求度的取值范围if degrange(1)==degrange(2)degrange(1)=degrange(1)-3;degrange(2)=degrange(2)+3;endpinshu=hist(deg,[degrange(1): degrange(2)]);%求度取值的频数ind=find(pinshu==0); %找频数为0的地址dp=[[degrange(1):degrange(2)]; pinshu]; %构造频数分布表%dp(:,ind)=[]; %删除频数为0的列df=dp(2,:)/N; %求度的频率分布figure, bar(dp(1,:),df,'r') %画度的频率分布柱状图title(s+" Degree Distribution");xlabel('$k$','Interpreter','Latex'), ylabel('$P$','Interpreter','Latex')
clc;clear;load NN.mat[D,L,dist]=myAPL(A);[TC,c]=mycluster(A);dp=mydegree(A,"NNC");M=sum(sum(A))/2d=dp(1,:)*dp(2,:)'/20LTC