介绍
教材推荐
《Nonlinear Dynamics and Chaos》
软件
画相位图的话,可以用 MATLAB,参考
- matlab如何画相图? - Longson的回答。
- http://matlab.cheme.cmu.edu/2011/08/09/phase-portraits-of-a-system-of-odes/
更推荐使用 dfield and pplane,有 online 版本的,但稍微缺少一点功能:
也有 MATLAB 版本的,但只适配 2018 版本,最新的 2020 是不支持的。
最好下载 Java 版本的,直接运行即可: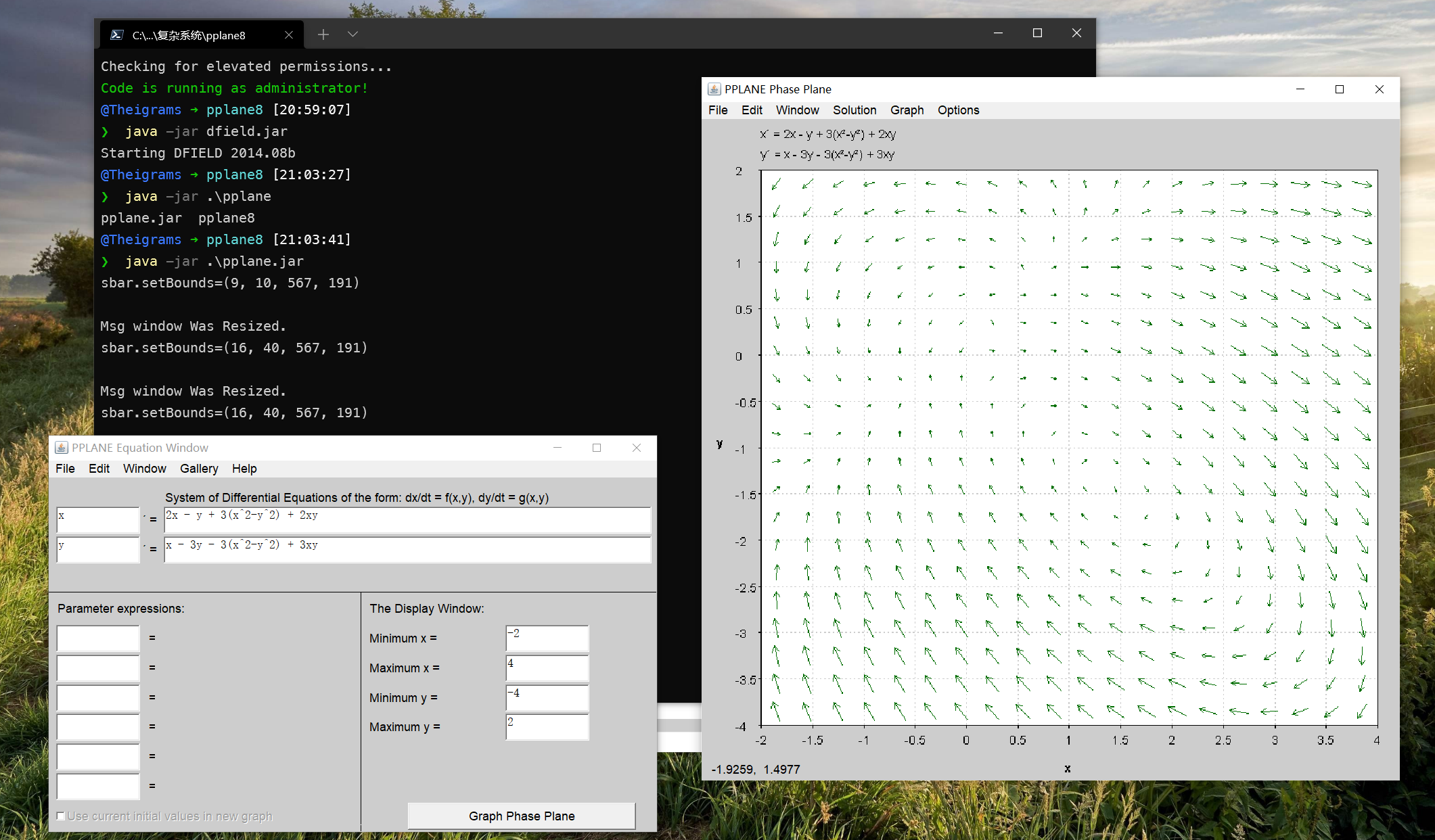
直线上的流
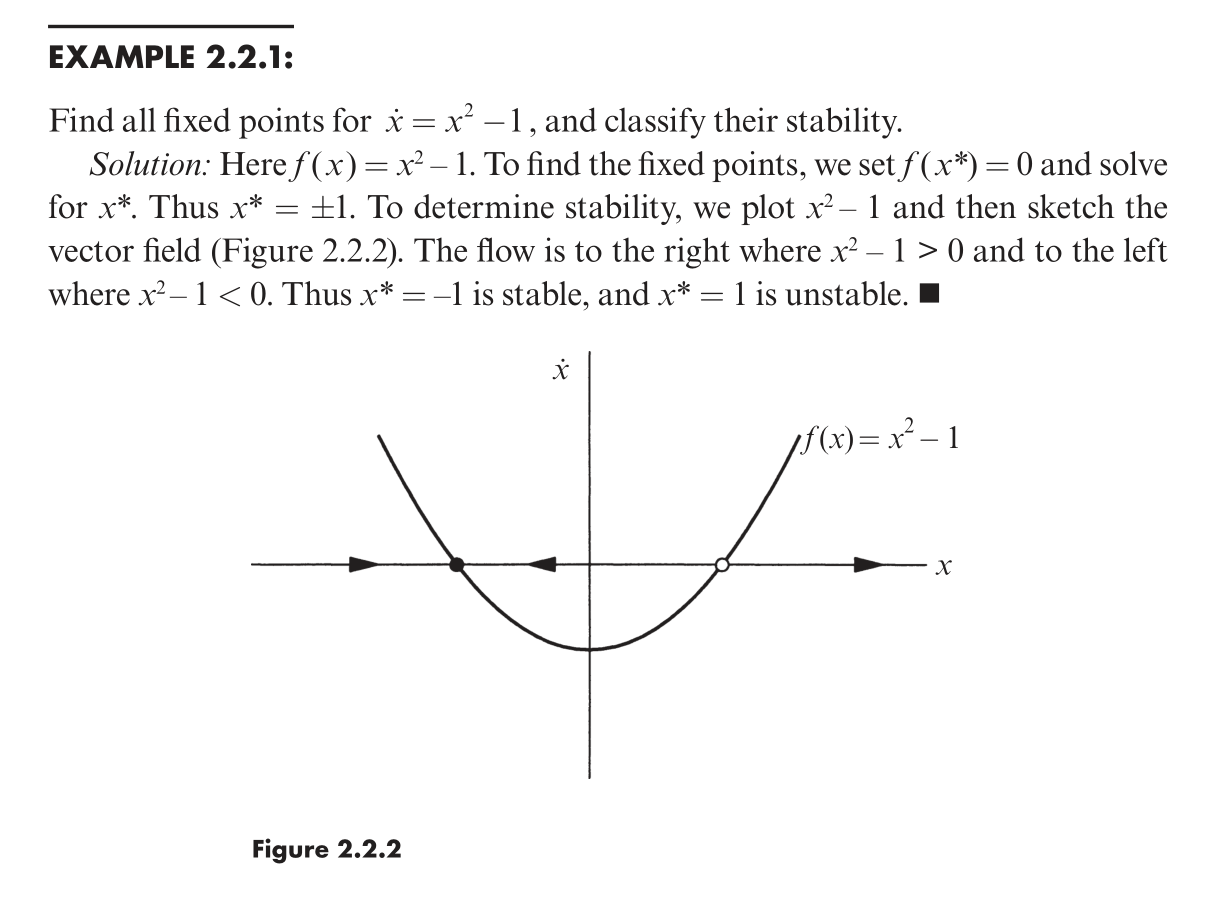
Fixed Points and Stability
Linear Stability Analysis

分岔 (bifurcations)
Saddle-Node Bifurcation
Graphical Conventions
对于不同的 r 有不同的向量场图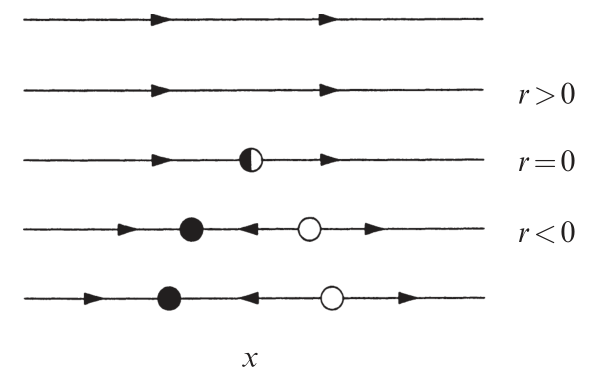
我们将其用 x-r 图像来描述
此处 r 为自变量,因此进行翻转:
Normal Forms
Saddle-Node Bifurcation 的结构都形如 ,因此对于一般的函数也可以通过泰勒展开转成标准型:

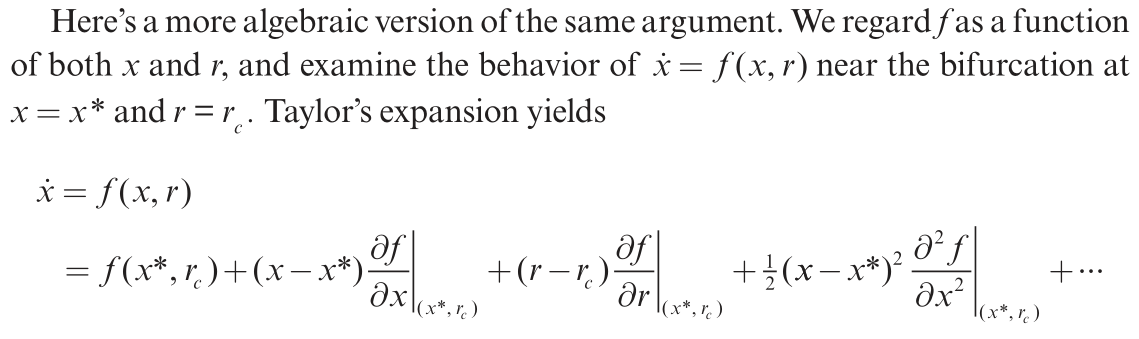

跨临界分岔 (Transcritical Bifurcation)
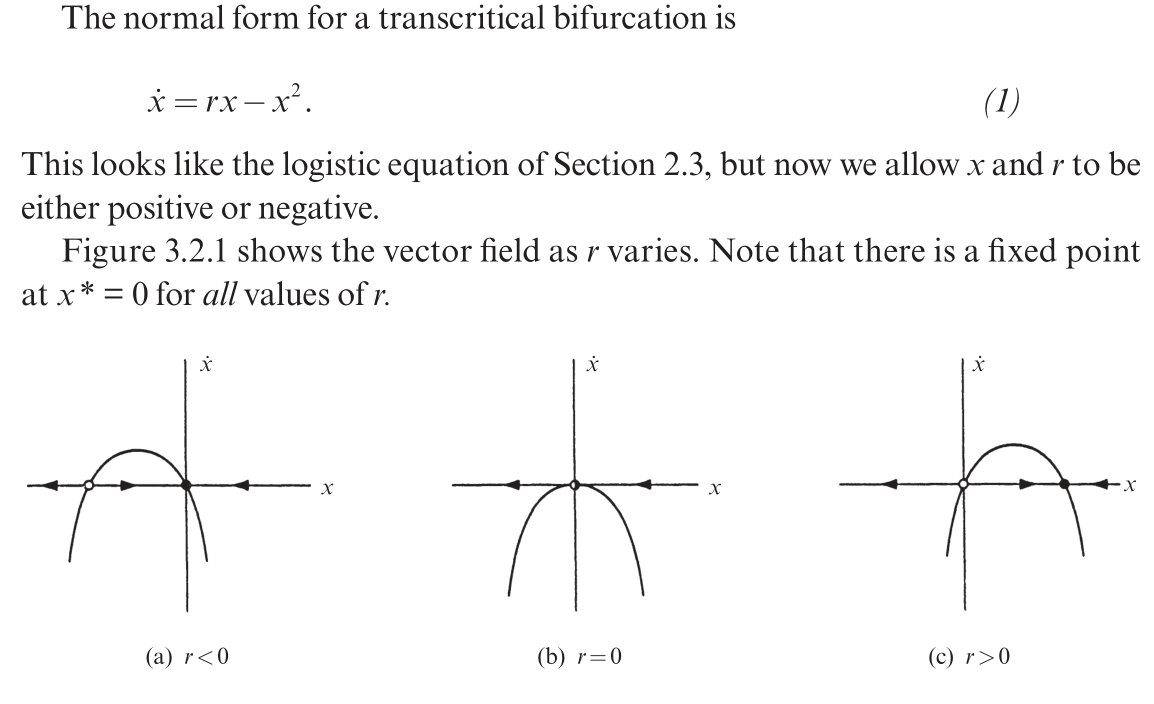
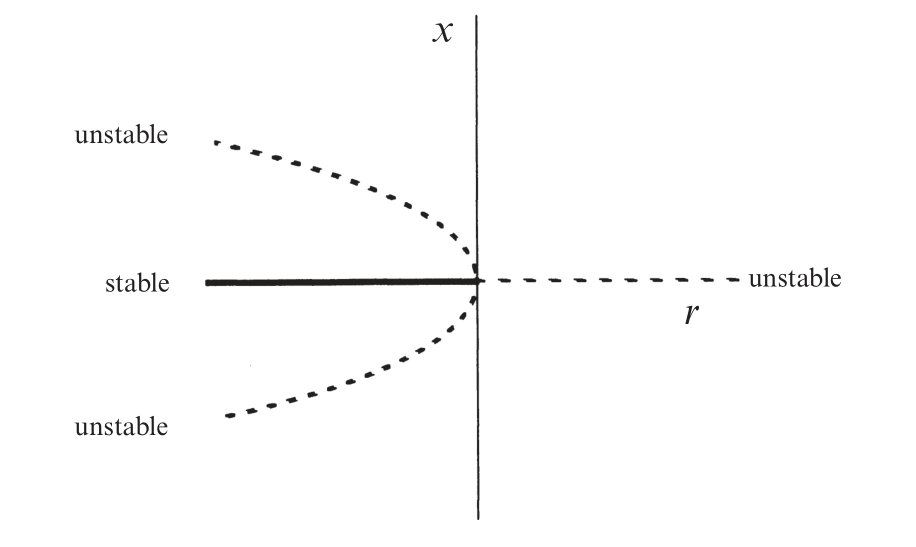
随着 r 从负变到正,不动点的稳定性也发生了变换,r =0 时左边的不稳定点与 x=0 的稳定点融合,变成了半稳定点。当 r >0 时,两个不动点的稳定性发生了交换。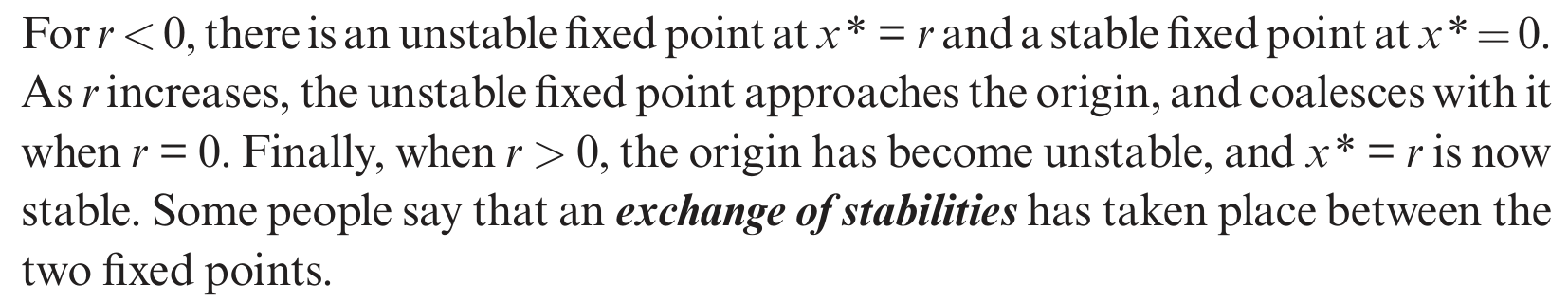
叉式分岔 (Pitchfork Bifurcation)
Supercritical Pitchfork Bifurcation

随着 r 的增大,不动点 x=0 的稳定性消失了!但增加了两个稳定点。
Subcritical Pitchfork Bifurcation
%22%20aria-hidden%3D%22true%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2D9%22%20x%3D%2263%22%20y%3D%222%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%22850%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-72%22%20x%3D%221906%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%20x%3D%222358%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%223152%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(4153%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-33%22%20x%3D%22809%22%20y%3D%22583%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=%5Cdot%7Bx%7D%3Drx%2Bx%5E3&id=JBAbF)
Imperfect Bifurcations and Catastrophes
%22%20aria-hidden%3D%22true%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2D9%22%20x%3D%2263%22%20y%3D%222%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%22850%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-68%22%20x%3D%221906%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%222705%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-72%22%20x%3D%223706%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%20x%3D%224157%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%224952%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(5952%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-33%22%20x%3D%22809%22%20y%3D%22583%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=%5Cdot%7Bx%7D%3Dh%20%2B%20rx%2Bx%5E3&id=FgqLp)
在超临界分岔的基础上加了个小常数项,会发生什么变化呢?
这是用 Mathematica 绘制出来的图像,这个不是函数图像,是 r-x 和 h-x 组合的立体化,从 h 轴的横截面来看,就是上面提到过的 r-x 图像。
ContourPlot3D[r*x - x^3 + h == 0, {r, -2, 2}, {h, -2, 2}, {x, -2, 2}, Mesh -> None, AxesLabel -> {r, h, x}, ContourStyle -> Directive[Orange, Opacity[0.8], Specularity[White, 30]]]
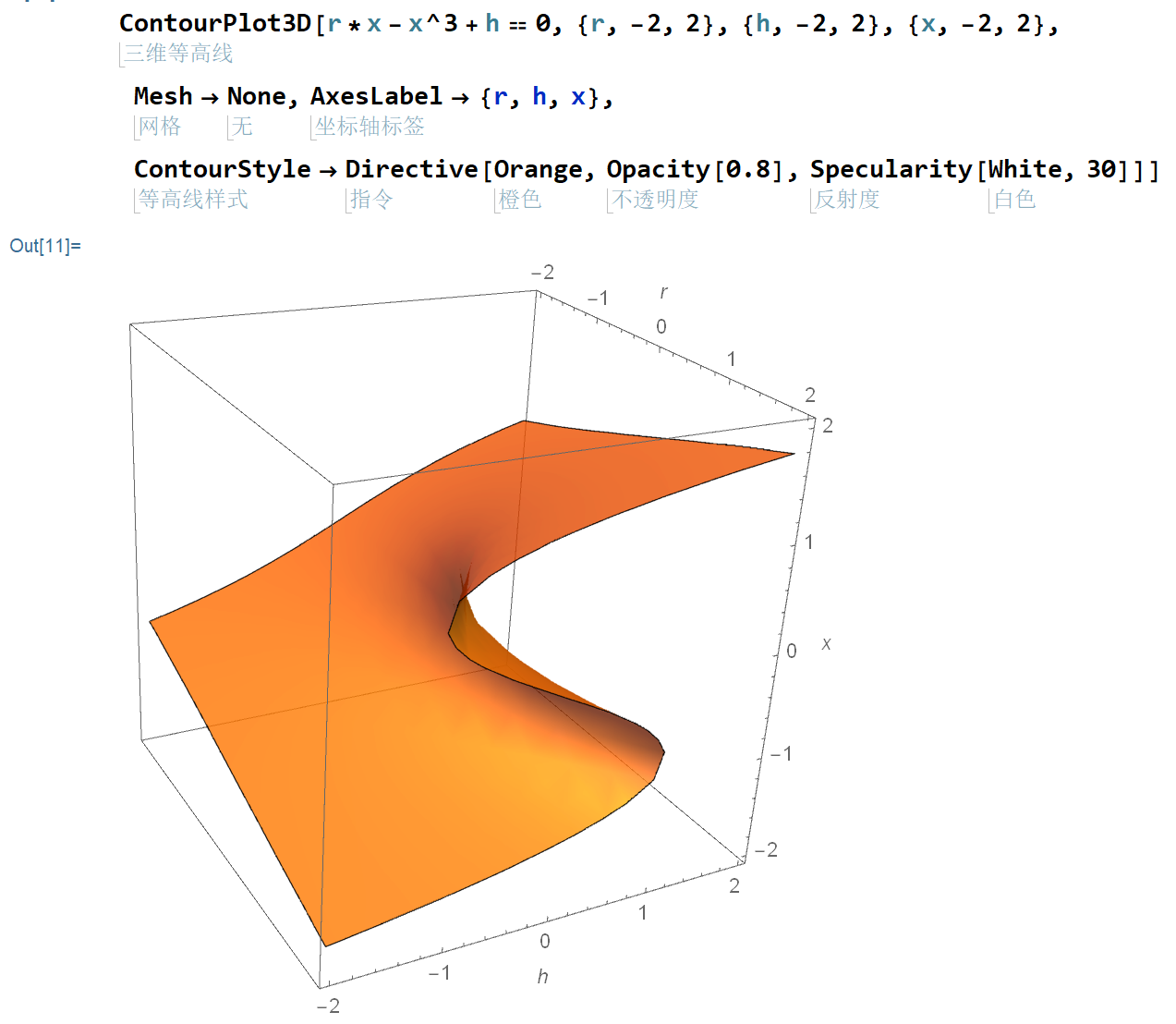

书中也对这个进行了说明,当点从 r-h 平面上运动时,对应的系统状态可能会从上表面突然滑落到下表面。
我对这个的理解也不大深刻,大概是这样,如果系统状态对应的是最大的那个不动点,但随着参数 (r,h) 的变化,一开始不动点也是慢慢随之变化,但到了一个临界点处,系统中原来的两个不动点都消失了,只剩下了一个下表面上的不动点,系统状态也就在此处发生了一个突变。
与之对应的,还有个不完全(不完美)跨临界分岔,也是在之前的跨临界分岔上加了个常数项。
ContourPlot3D[r*x - x^2 + h == 0, {r, -2, 2}, {h, -2, 2}, {x, -2, 2}, Mesh -> None, AxesLabel -> {r, h, x}, ContourStyle -> Directive[Orange, Opacity[0.8], Specularity[White, 30]]]

最后推荐一个小讲义,写得还算清晰明了DynSysLecture2.pdf