降秩回归 (Reduce-Rank Regression)

最小二乘回归

首先介绍一下最小二乘回归，对于

我们有


从几何的角度来看，就是寻找b在A列空间中的投影

A 将 b 分成了两部分，一部分属于A的列空间，另一部分垂直于A的列空间

由垂直可知：


得到了同样的结论

Reduce-Rank Regression

降秩回归与最小二乘回归有点类似，问题变成了

并且对 B 的秩有要求：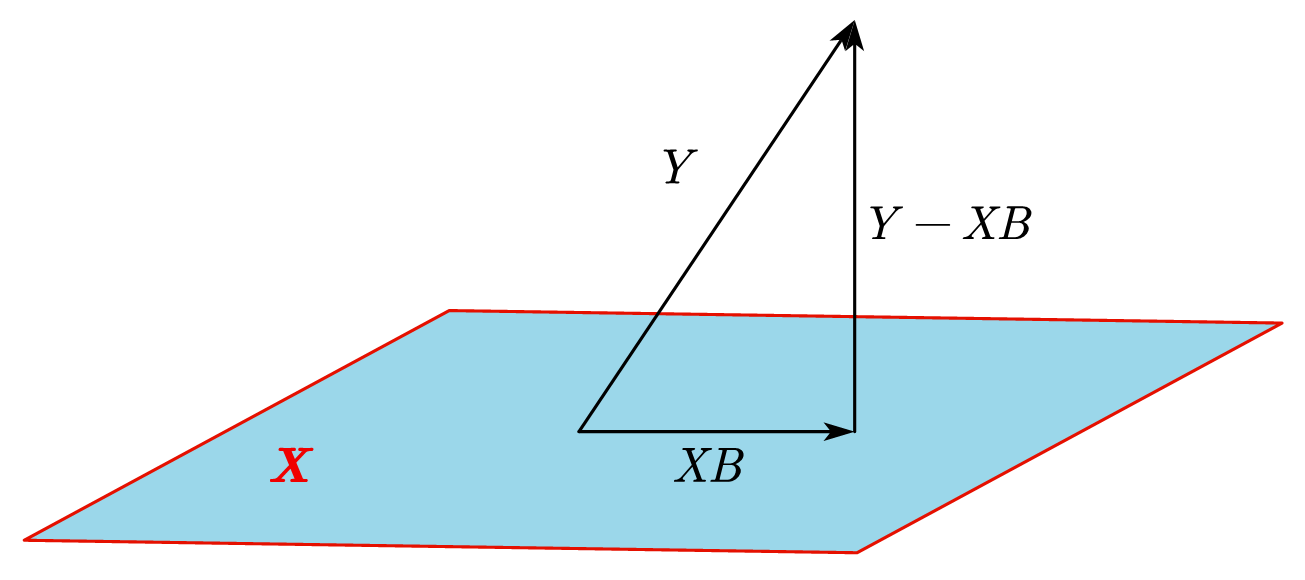

我们先设其最小二乘解为 ，于是有


我们知道 是垂直 X 的，所以内积项为0。
而 与 B 无关，所以只需考虑第二项：

我们设 ，于是问题就变成了求 的减秩逼近。

我们其进行SVD分解：，在 F 范数下， 的秩r最优逼近为

我们设 ，，于是有

于是 即为所求。

注意

这里要注意以下几点：

1. 为什么不直接用 XB 去逼近 Y，而是去逼近，因为需要满足行满秩。

2. 忘了，等想起来再补充

   参考

3. What is “reduced-rank regression” all about?

4. Mukherjee, 2013, Topics on Reduced Rank Methods for Multivariate Regression