机器学习算法 = 模型表征+模型评估+优化算法

例子： 支持向量机=线性分类模型+最大间隔 逻辑回归对应=线性分类模型+交叉熵。

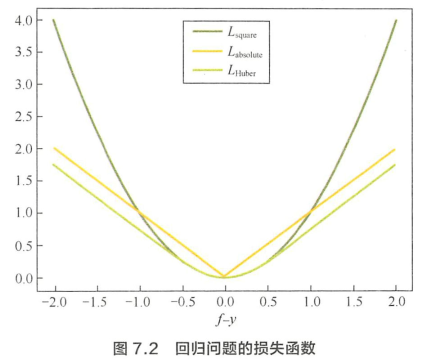
监督学习涉及的损失函数有哪些?

《百面机器学习》P142

• 二分类问题
  • 0-1损失
    • 非凸、非光滑，难以优化
  • Hinge损失
    • 凸，在fy≥1时不做任何惩罚，在fy=1处不可导，不能用gradient descent优化，而是用subgradient descent
  • logistc损失
    • 凸，处处光滑，可以用gradient descent优化，但其对所有样本点都有所惩罚，因此对异常值相对敏感一些
• 分类问题
  • 
    
    • 光滑

• 回归问题
  • 平方损失
    • 光滑，可用GD优化
    • 当预测值距离真实值越远时，惩罚力度越大，因此对异常点比较敏感
  • 绝对损失
    • 对异常点相对更鲁棒一些
    • 在f=y处无法求导
  • Huber损失
    • 较小时为平方损失，较大时为线性损失，对异常点鲁棒
    • 处处可导

机器学习中的优化问题，哪些是凸优化问题，哪些是非凸优化问题？举例子

《百面》P145

• 凸优化：
  • 逻辑回归：损失函数的海塞矩阵半正定
  • 支持向量机
  • 线性回归

• 非凸优化：

  • 深度神经网络

    无约束的优化算法有哪些？

    《百面》P148

• 直接法

  • 需要满足两个条件
    • 损失函数L为凸函数
    • L有解析解

  • 求解方法

    • 求解充分必要条件：

      例子：岭回归

• 迭代法

  • 一阶迭代：Gradiet Descent 《机数》P185 算法4.1
    • 动机：L不是凸函数/没有解析解，不能直接求解
    • 思想：根据泰勒展开，得出函数下降最快的方向为梯度反方向
  • 二阶迭代：牛顿法《机数》P192 算法4.2
    • 动机：GD只利用了一阶导数信息，收敛速度慢
    • 思想：根据泰勒展开，在每个迭代点处将目标函数近似为二次函数，求解梯度为0的点。因为这是函数的近似，所以得到的不一定是驻点，而是迭代方向。
    • 问题：
      • 无法保证每次迭代时目标函数值下降
      • 需要计算梯度和黑塞矩阵，计算成本更高
      • 黑塞矩阵不一定可逆
    • 优点：收敛速度更快
  • 拟牛顿法：牛顿法的改进
    • 思想：不精确计算目标函数的黑塞矩阵然后求逆，而是通过其他手段得到黑塞矩阵的逆。

      《机器学习的数学》4.2, 4.3 CS7015 Lecture 5

如何验证求目标函数梯度功能的正确性?

《百面》P152，不好理解

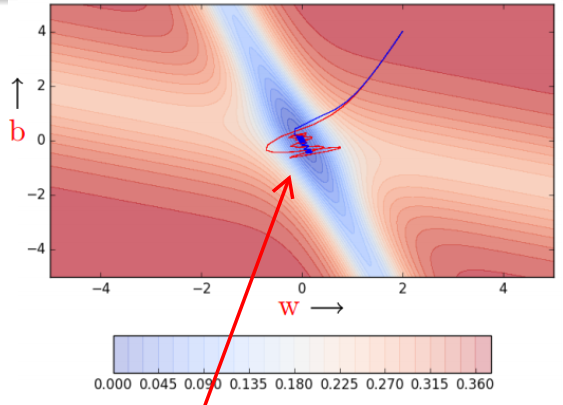
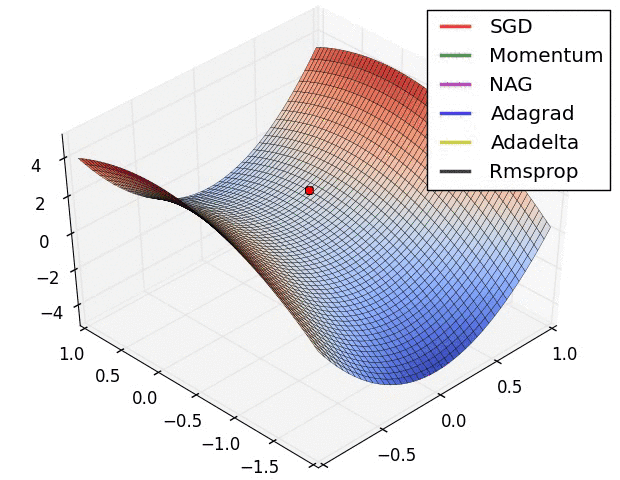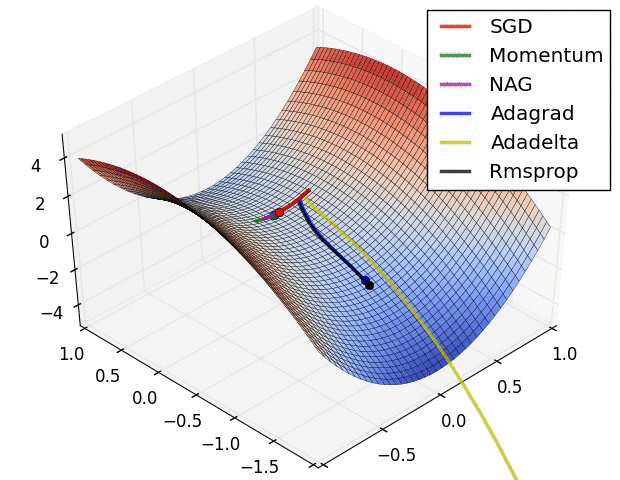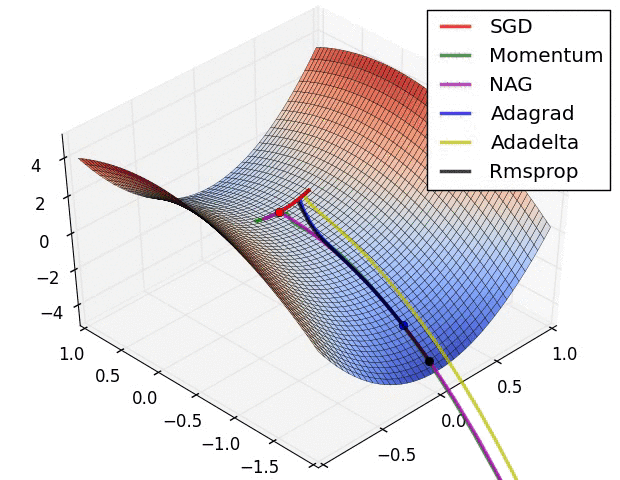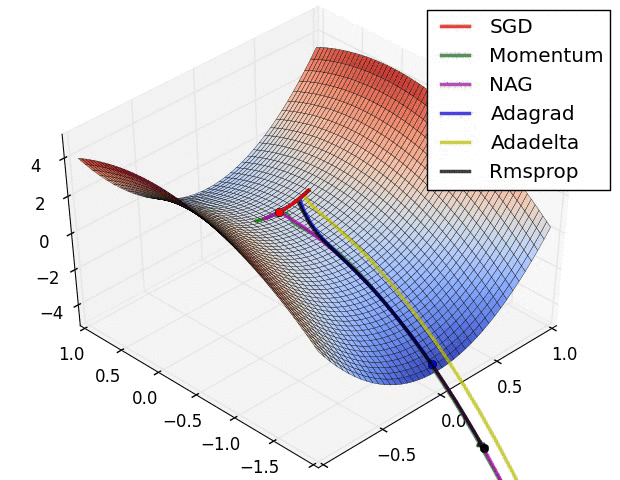
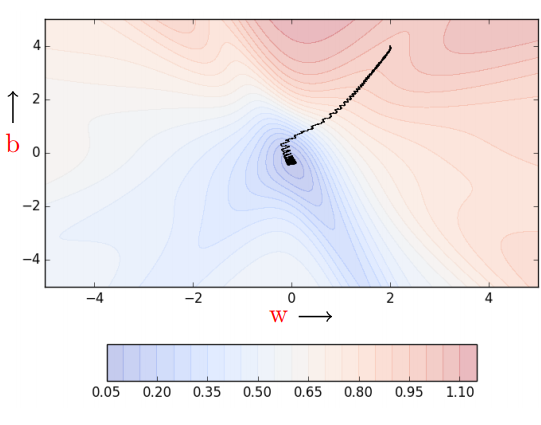
Gradient Descent的三个问题及改进

deep learning book CS7015 Lecture 5 《百面》P158 写得很好！！

Q1

Stochastic GD

• Problem: 基础的GD算法每次更新梯度时，考虑所有的训练点，当数据集非常大时，计算量非常大
• Solution: Stochastic GD
  • updates the parameters for every single data point
  • Stochastic because we are estimating the total gradient based on a single data point. Almost like tossing a coin only once and estimating P.
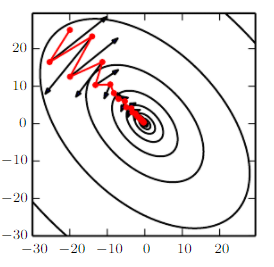
• New Problem: many oscillations

• Cause:

Stochastic does not guarantee that each local greedy move reduces the global error

Mini-Batch GD

• Reason: more data, more accurate stochastic estimates of the gradient
• Solution:

Q2

Momentum based GD

• Problem: It takes a lot of time to navigate regions having a gentle slope
• Cause: because the gradient in these regions is very small
• Reason:

类比到物理的物体运动，w是位置，update是速度，运动时间t=1，w的梯度是加速度，系数*w的梯度就是速度的变化量。每次运动的时候加入历史的速度，即加入惯性。

• Solution: Momentum based GD

• Benifit:
  • 在梯度变化小的地方，更新得更快
  • 在stochastic GD到山谷时，可以减少oscillation

Nestrov Accelerated GD

• New Problem: Momentum oscillates in and out of the minima valley as the momentum carries it out of the valley, takes a lot of u-turns before finally converging.

• Reason: Look ahead before leap, correcting its course quicker than momentum based gradient descent.
• Solution: Nestrov Accelerated GD

• Benifit:
  • the oscillations are smaller, the chances of escaping the minima valley also smaller

Q3

Adaptive Learning(Adagrad)（环境感知）

• Problem: If some feature happens to be sparse as well as important we would want to take the updates to its parameter more seriously

example: 一开始特征稀疏的参数w更新很少

• Solution: Adagrad

Decay the learning rate for parameters in proportion to their update history

• Benifit: despite sparsity, w gets a higher learning rate and hence larger updates
  
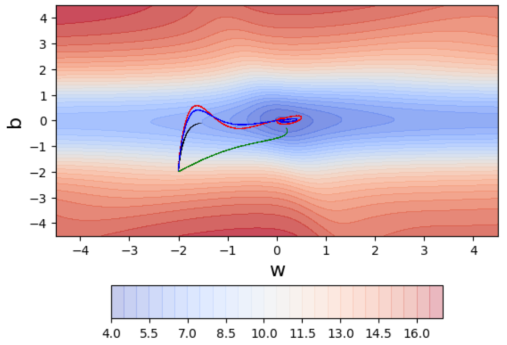
• New Problem: Adagrad decays the learning rate very aggressively. after a while the frequent parameters will start receiving very small updates because of the decayed learning rate

RMSProp

• Solution: decay the denominator and prevent its rapid growth
  

Adam

• Reason:
  • 
    
• Solution: Do everything that RMSProp does to solve the decay problem of Adagrad. Plus use a cumulative history of the gradients

In pratice,

鞍点问题

其他问题

训练数据量特别大时经典梯度法存在的问题,如何改进?

《百面》 P155 mini-batch

随机梯度下降法失效的原因。

《百面》P158

如何验证求目标函数梯度功能的正确性?

《百面》P152