集成学习

偏差与方差

• 偏差指的是由所有采样得到的大小为m的训练数据集训练出的所有模型的输出的平均值和真实模型输出之间的偏差。偏差通常是由于我们对学习算法做了错误的假设所导致的，比如真实模型是某个二次函数，但我们假设模型是一次函数。由偏差带来的误差通常在训练误差上就能体现出来。

• 方差指的是由所有采样得到的大小为m的训练数据集训练出的所有模型的输出的方差。方差通常是由于模型的复杂度相对于训练样本数m过高导致的，比如一共有100 个训练样本，而我们假设模型是阶数不大于200的多项式函数。由方差带来的误差通常体现在测试误差相对于训练误差的增量。

简单介绍一下bagging，常用bagging算法有哪些？

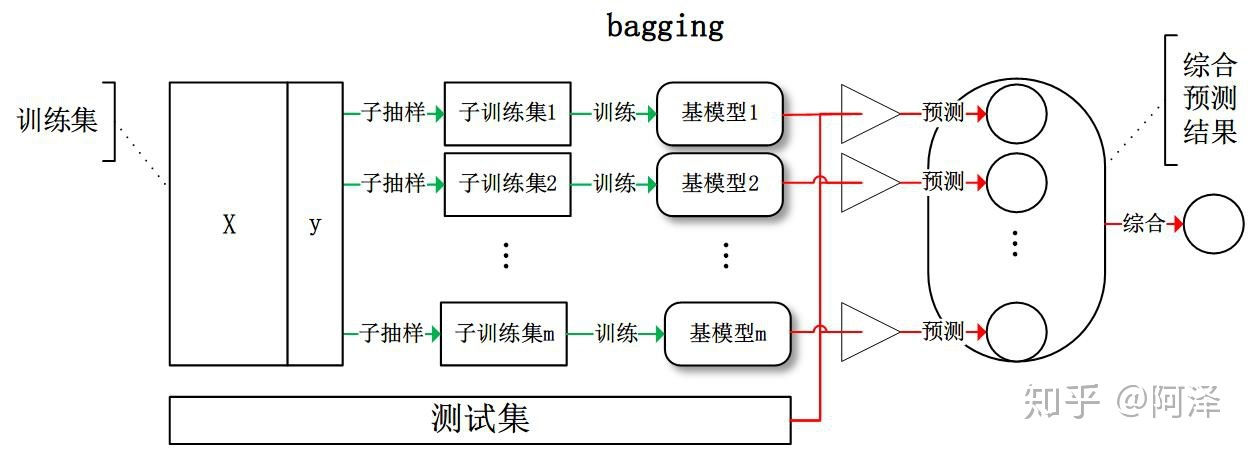
• 含义
  • 多次采样，训练多个分类器，集体投票，旨在减小方差，各个学习器之间相互独立、可同时生成的并行化方法。
• 算法流程

输入：样本集%EF%BC%8C(x_2%EF%BC%8Cy_2)%20%5Cdots%20(x_m%EF%BC%8Cy_m)%7D#card=math&code=D%3D%7B%28x_1%EF%BC%8Cy_1%29%EF%BC%8C%28x_2%EF%BC%8Cy_2%29%20%5Cdots%20%28x_m%EF%BC%8Cy_m%29%7D&id=XmzkV)，弱学习器算法，弱分类器迭代次数。
输出：为最终的强分类器#card=math&code=f%28x%29&id=O9YdH)

• 对于
• 对训练集进行第t次随机采样，共采集次，得到包含个样本的采样集
• 用采样集训练第个弱学习器#card=math&code=G_t%28x%29&id=Uh2J6)
• 如果是分类算法预测，则个弱学习器投出最多票数的类别或者类别之一为最终类别；如果是回归算法，个弱学习器得到的回归结果进行算术平均得到的值为最终的模型输出。
  • 常用bagging算法：随机森林算法

简单介绍一下boosting，常用boosting算法有哪些？

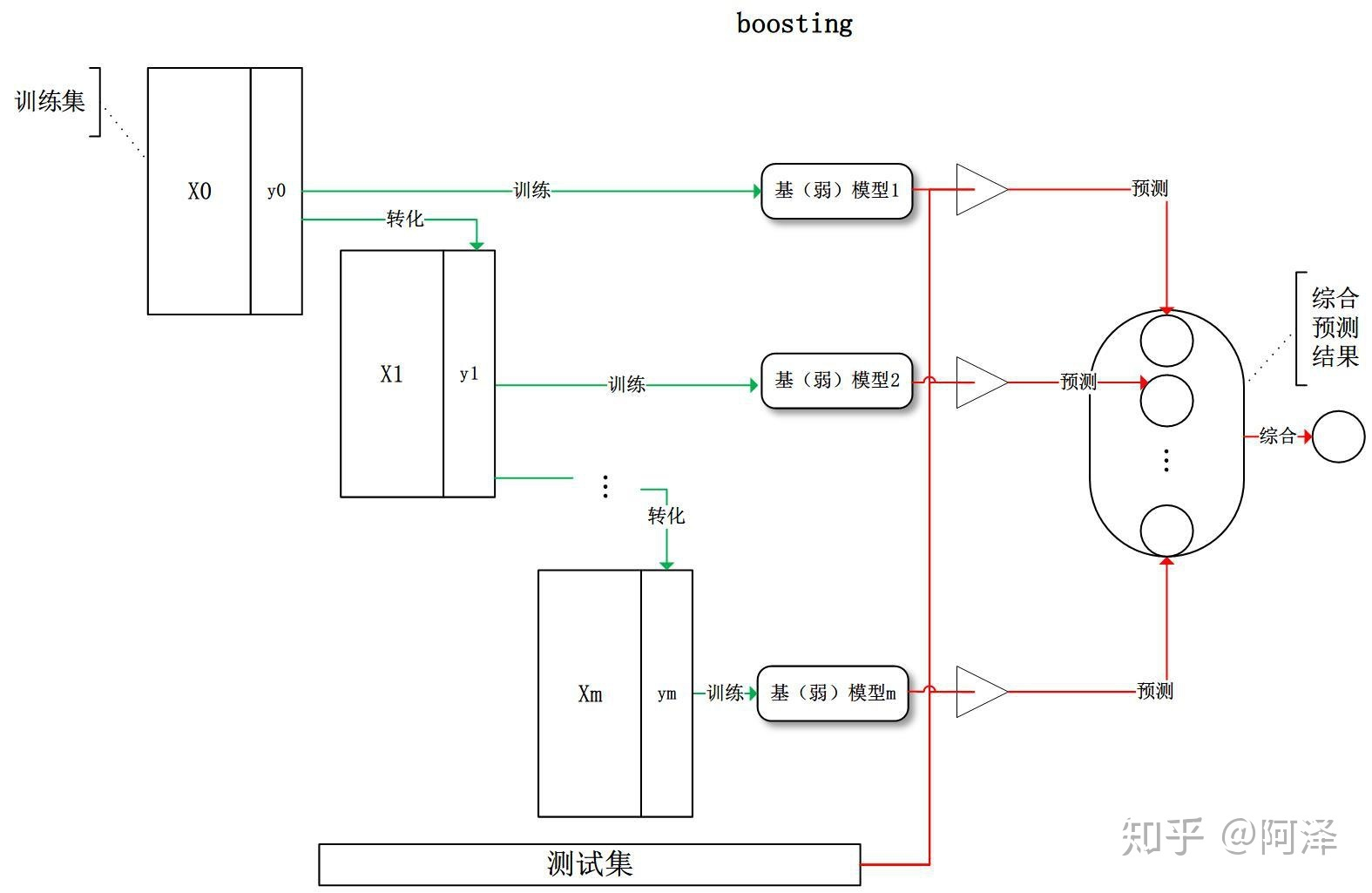
• 含义

基分类器层层叠加，聚焦分错的样本，旨在减小偏差。个体学习器是串行序列化生成的、具有依赖关系，它试图不断增强单个学习器的学习能力。

• 算法流程：
  • 给定初始训练数据，由此训练出第一个基学习器；
  • 根据基学习器的表现对样本进行调整，在之前学习器做错的样本上投入更多关注；
  • 用调整后的样本，训练下一个基学习器；
  • 重复上述过程T次，将T个学习器加权结合。
• 常用boosting算法：
  • Adaboost
  • GBDT
  • XGBoost

boosting思想的数学表达式是什么？

%3Dw%7B0%7D%2B%5Csum%7Bm%3D1%7D%5E%7BM%7D%20w%7Bm%7D%20%5Cphi%7Bm%7D(x)%0A#card=math&code=f%28x%29%3Dw%7B0%7D%2B%5Csum%7Bm%3D1%7D%5E%7BM%7D%20w%7Bm%7D%20%5Cphi%7Bm%7D%28x%29%0A&id=B8IYF)

其中是权重，是弱分类器的集合，可以看出最终就是基函数的线性组合。

简单介绍一下stacking

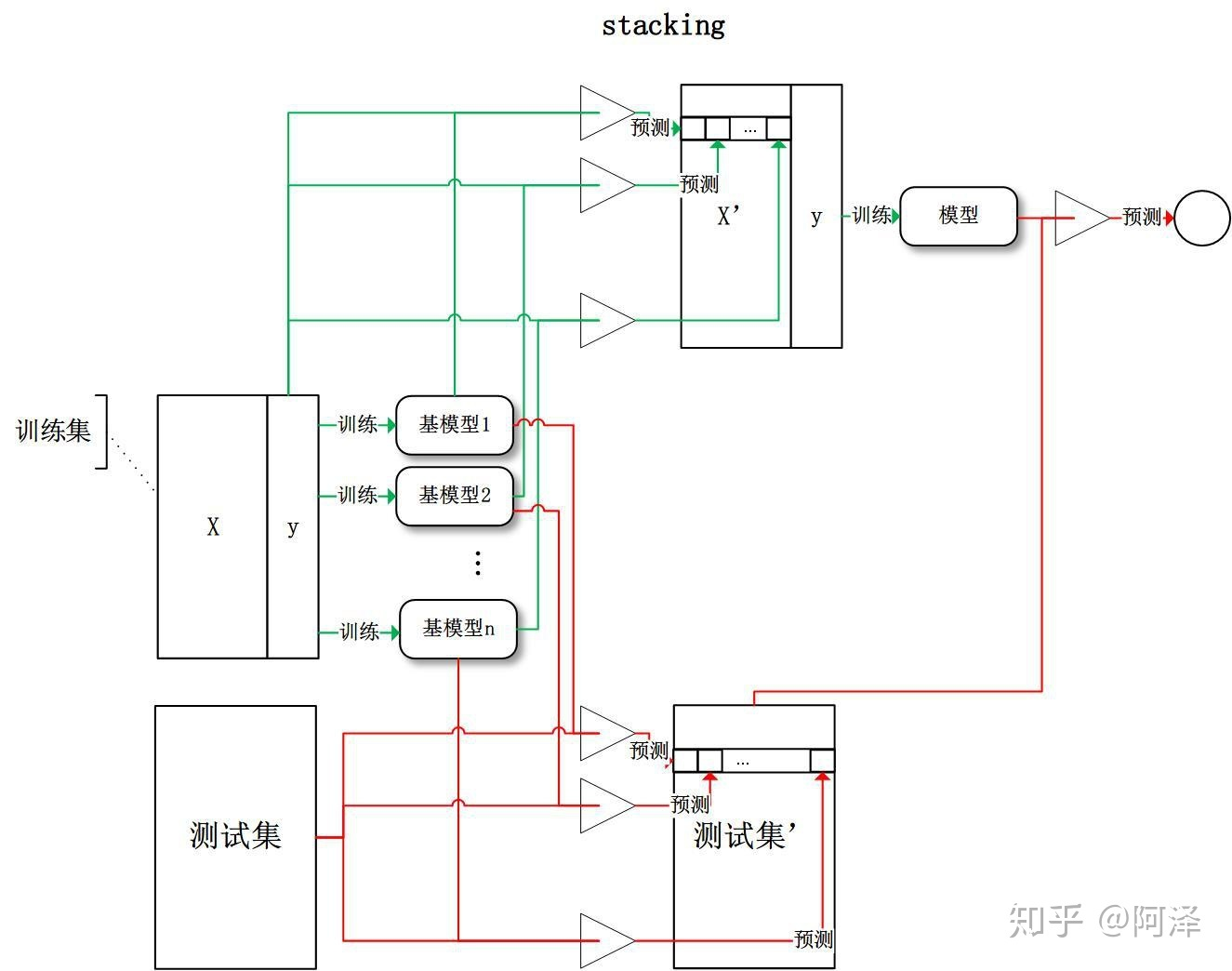
Stacking 是先用全部数据训练好基模型，然后每个基模型都对每个训练样本进行的预测，其预测值将作为训练样本的特征值，最终会得到新的训练样本，然后基于新的训练样本进行训练得到模型，然后得到最终预测结果。

你意识到你的模型受到低偏差和高方差问题的困扰，应该使用哪种算法来解决问题呢？为什么？

在这种情况下，我们可以使用bagging算法（如随机森林），以解决高方差问题。bagging算法把数据集分成重复随机取样形成的子集。然后，这些样本利用单个学习算法生成一组模型。接着，利用投票（分类）或平均（回归）把模型预测结合在一起。另外，为了应对大方差，我们可以，使用正则化技术，惩罚更高的模型系数，从而降低了模型的复杂性。

常用的基分类器是什么？（查

最常用的基分类器是决策树，原因:

• 决策树可以较为方便地将样本的权重整合到训练过程中，而不需要使用过采样的方法来调整样本权重。
• 决策树的表达能力和泛化能力，可以通过调节树的层数来做折中。
• 数据样本的扰动对于决策树的影响较大，因此不同子样本集合生成的决策树基分类器随机性较大，这样的“不稳定学习器”更适合作为基分类器。此外，在决策树节点分裂的时候，随机地选择一个特征子集，从中找出最优分裂属性，很好地引入了随机性。

如何从减小方差和偏差的角度解释Boosting和Bagging的原理？

再摘抄《百面》
再看Boosting，在训练好 一个弱分类器后，我们需要计算弱分类器的错误或者残差，作为下一个 分类器的输入。这个过程本身就是在不断减小损失函数，来使模型不断 逼近“靶心”，使得模型偏差不断降低。但Boosting的过程并不会显 著降低方差。这是因为Boosting的训练过程使得各弱分类器之间是强 相关的，缺乏独立性，所以并不会对降低方差有作用。