1 Spectral clustering 谱聚类概述
援引文章的一段话:
谱聚类(spectral clustering)是广泛使用的聚类算法,比起传统的K-Means算法,谱聚类对数据分布的适应性更强,聚类效果也很优秀,同时聚类的计算量也小很多,更加难能可贵的是实现起来也不复杂。在处理实际的聚类问题时,个人认为谱聚类是应该首先考虑的几种算法之一。
谱聚类是从图论中演化出来的算法,如果对于图神经网络 GNN 中基于频谱(spectral-based)的方法比较熟悉的话,则这一部分将会轻松拿下;当然如果掌握了这一部分的内容,基于频谱的 GNN 也可以轻松拿下。
谱聚类的主要思想是,把每一个数据点看作一个图中的节点,他们之间通过被赋予权重的边所连接,而谱聚类的目标就是希在图上望找到 k 不相交个子图(节点集合的划分)来作为 k 个簇,以此对节点进行聚类。例如下图中,我们将整个图划分为两个子图 A 和 B,即可将子图 A 和子图 B 中的节点分别聚为一类。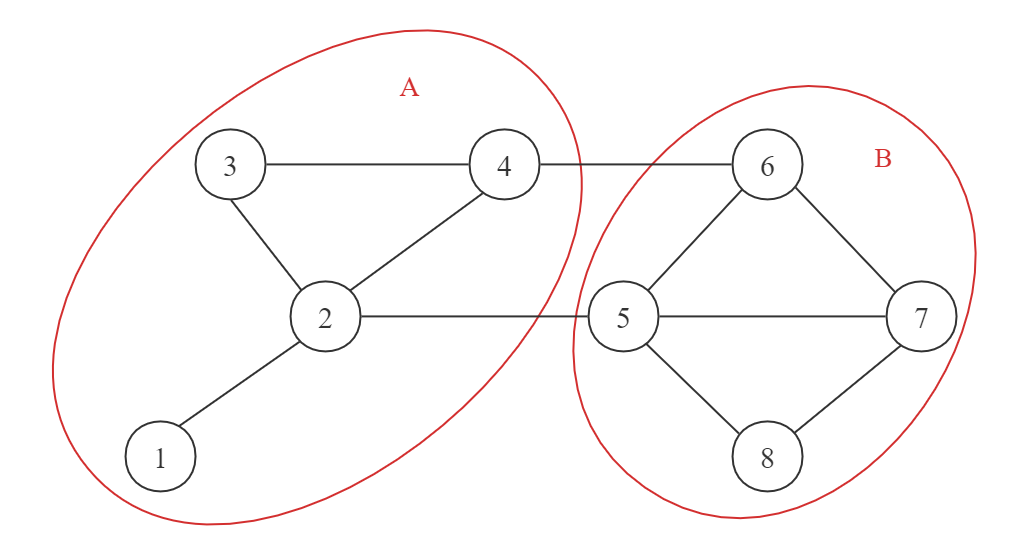
2 数学基础 —— 图上的矩阵
在图论中,我们一般将一个图表示为%22%20aria-hidden%3D%22true%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-47%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%221064%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%222120%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-56%22%20x%3D%222510%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%20x%3D%223279%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-45%22%20x%3D%223724%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%224489%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=G%20%3D%20%28V%2C%20E%29&id=S2XBB)的二元组,其中
和
%22%20aria-hidden%3D%22true%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-45%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%221042%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-7B%22%20x%3D%222098%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%222599%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-75%22%20x%3D%222988%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%20x%3D%223561%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-76%22%20x%3D%224006%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%224491%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2223%22%20x%3D%224881%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-75%22%20x%3D%225159%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%20x%3D%225732%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-76%22%20x%3D%226177%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2208%22%20x%3D%226940%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-56%22%20x%3D%227885%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-7D%22%20x%3D%228655%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=E%20%3D%20%5C%7B%28u%2C%20v%29%20%7C%20u%2C%20v%20%5Cin%20V%5C%7D&id=s4IZL)分别是图的节点和边集合。在图结构的分析与计算中,矩阵扮演了最重要的图信息存储的角色。可以说,在计算机中,图就是被存储在矩阵中的,即图可以用特殊的矩阵进行表示。
- 邻接矩阵
其中如果 直接有边,则
就是这两个节点之间的权重;一般谱聚类中都假定我们形成的图是无向图,则
,
则是一个对称矩阵。
- 节点度矩阵
其中,即与节点
相连所有边的权重之和。同时可以注意到,节点度矩阵
是一个对角阵。
- 拉普拉斯矩阵
拉普拉斯矩阵(Laplacian matrix)可算是图计算、信号分析领域的老熟人了,基于频谱的 GNN 中核心技术之一就是拉普拉斯矩阵了。拉普拉斯矩阵有很多非常好的性质:
是对称阵,则两个不同的特征向量相互正交
- 对任意向量
有
其中可以用来作为对
个节点的特征向量,比如
就代表了节点
的属性值。
这样就是一个半正定矩阵,具有一些不错的性质。对于上式证明如下:
我们可以看到,如果
是代表节点信号强度的向量(如
代表
节点信号强度),则
则可以看作是图中所有节点的加权平滑程度(或总体差异)的度量。
3 谱聚类问题建模
3.1 相似矩阵
可以看到,不管是节点的度矩阵还是拉普拉斯矩阵
,都是以邻接矩阵
为基础才能求出的。那么问题就来了,我们模型的输入,也就是数据预处理的结果,只有
个点的特征向量,而没有这
个节点之间的权重,该如何构建邻接矩阵
呢?
基本思想就是,距离越远的两个点之间的边权重较低,而距离较近的两个点之间权重值较高。所以一般通过计算相似矩阵来获得邻接矩阵
。常见的有三类:ε-邻近法、K 近邻法以及全连接法,最常用的就是全连接法,下面将仅对全连接法进行介绍,其他两种可以参考文章。
在全连接法中,任意两点之间的权重都大于 0,因此被称为全连接法。全连接法通过选择不同的核函数来定义边的权重,常用的有多项式核函数、高斯核函数(RBF)和 Sigmoid 核函数等。最常用的就是高斯核函数 RBF,此时邻接矩阵和相似矩阵相同:
3.2 谱聚类的数学模型
对于无向图,我们首先将其划分成 k 个子图,且子图之间没有重复的节点,这 k 个子图的节点集记作
,且
,
。
对于任意两个节点集合,我们将它们两个之间的权重定义为
谱聚类的思想就是,最小化任意两个子图节点集之间的权重和。由此,我们定义对于的切图:
%22%20aria-hidden%3D%22true%22%3E%0A%3Cg%20transform%3D%22translate(-11%2C0)%22%3E%0A%3Cg%20width%3D%2250%25%22%3E%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(789%2C0)%22%3E%0A%3Cg%20transform%3D%22translate(10841%2C-88)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-63%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-75%22%20x%3D%22433%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-74%22%20x%3D%221006%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%221367%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(1757%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-56%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%22825%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%20x%3D%222794%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(3239%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-56%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-32%22%20x%3D%22825%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%20x%3D%224276%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2026%22%20x%3D%224722%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%20x%3D%226061%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(6506%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-56%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6B%22%20x%3D%22825%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%227558%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%228226%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(9282%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ1-2211%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-6B%22%20x%3D%221494%22%20y%3D%22675%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(1056%2C-287)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%22345%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%221124%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-57%22%20x%3D%2211754%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%2212802%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(13192%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-56%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%22825%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%20x%3D%2214119%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(14565%2C0)%22%3E%0A%3Cg%20transform%3D%22translate(35%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-56%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%22825%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(0%2C248)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-AF%22%20x%3D%22-70%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(321.37818613144964%2C0)%20scale(0.5700980412741057%2C1)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-AF%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-AF%22%20x%3D%22497%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%2215562%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(39225%2C0)%22%3E%0A%3Cg%20width%3D%2250%25%22%3E%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(40025%2C0)%22%3E%0A%3Cg%20transform%3D%22translate(869%2C-88)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%22389%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%22890%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=cut%28V1%2C%20V_2%2C%20%5Cldots%2C%20V_k%29%20%3D%20%5Csum%7Bi%3D1%7D%5Ek%20W%28V_i%2C%20%5Coverline%7BV_i%7D%29%20%5Ctag%7B1%7D&id=E8hdJ)
其中是
的补集,即
谱聚类的目标就是最小化 :
4 谱聚类算法
直接优化 是有问题的,比如下图中
Cut 1的切法将整个节点集划分为两个子集:和
,这样就可做到
的目标。然而这并不是我们想要的,我们更想要的是
Cut 2的划分方式。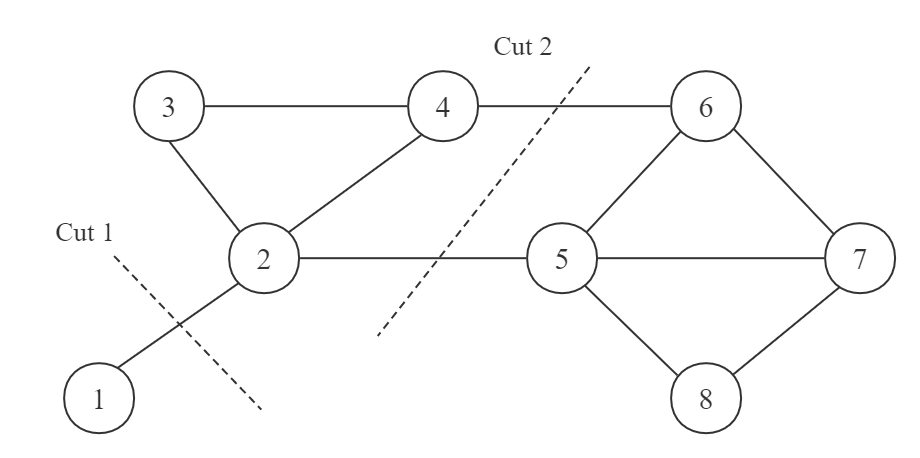
上面直接优化问题所在,就是没有考虑我们还需要一个簇内的节点个数不能太少。对于上述优化目标的改进与求解,于是就有了以下两个常见的谱聚类算法。
4.1 RatioCut 切图
RatioCut 切图为了解决上述一个簇内节点数过少的问题,同时还在目标函数中加入了每一个簇的节点个数的约束,即:
为了最小化这个函数,就有牛人提出了以下的解法。
首先我们引入指示变量 ,其中
为图中节点的个数,也就是需要聚类的样本点数。我们定义
即
的第
个分量为
即如果节点在
这个节点簇中,则
,否则就等于 0。
经过简单的推导,我们可以得到,其实构成了一组单位正交基,因为:
首先,中有
个非零元,而且这些非零元的数值都是
,所以
其次,因为和
中没有重复的节点,所以
。
如果我们计算则有:
由于,所以
。
我们将所有的放到一个矩阵中组成
,可以得到:
其中是矩阵
的迹(trace)。同时注意到
,所以我们等价的优化目标变成了
即需要找到矩阵使得
是最小的。
注意到矩阵中一共有
个指示向量,而每个指示向量中有
个元素,每个元素的取值为
或者
,所以总体的搜索空间是
,是个 NP 难问题。那么如何近似求解这个问题呢?
如上面的分析中提到的,的每一个子优化目标是
,其中所有的
构成一组单位正交基。又由于
是对称矩阵,所以
的两两不相同的特征向量也是正交的。故
的最大值就是
的最大特征值,
的最小值也是
的最小的特征值。这一点证明如下:
设是
的一组特征值和特征向量,即
进而有
如果对进行标准化,那么它依然是
特征值为
的特征向量:
进而有
得证的最大值就是
的最大特征值,
的最小值也是
的最小的特征值。
对于,我们的目标就是找到
的最小特征值,其对应的特征向量就是解
;而对于
,我们的目标就是找到
个最小的特征值及其对应的特征向量,一般来说
。这样我们利用维度规约的思想,将矩阵
规约成了
,近似求解了这个 NP 难问题。多提一句,以前矩阵
中的每一行
,可以被看作是节点
的特征向量;而在矩阵
中的每一行
成为了节点
新的特征向量。相当于我们将每一个节点进行了降维表示。
最后一般还要对矩阵按行进行标准化:
因为每一个行向量代表
的特征向量,而
代表节点
在第
个簇中的权重,所以我们要按行进行标准化。
由于在维度规约的过程中我们损失了一些信息,导致优化得到的指示向量矩阵不能完全指示个样本的归属(因为现在每一个列向量
已经不是非
即
的了)。所以我们需要对
个节点在进行一次 K-Means 一类的传统聚类算法,用每个行向量
作为节点
的特征向量。
4.2 Ncut 切图
Ncut 切图和 RatioCut 切图思路非常像:由于 RatioCut 只考虑到每一个簇的节点不能太少,但一个子图的节点个数多并不能代表这个子图的权重就一定大。所以 Ncut 切图基于每一个子图的权重不能太小为额外优化目标的思路进行聚类。
记 ,即子图
中所有节点的度权重之和,Ncut 希望最小化的目标函数为
同样使用 RatioCut 中优化的 trick,只是更改了指示变量的表示:
同样的推导方式,有 。所以我们的优化目标依然是 (5) 式
但现在的指示变量有一个问题只是相互正交,但不是单位向量,所以不能直接用 RatioCut 中降维的思想。而想用维度规约的思想,只需要对指示向量矩阵
做一个小小的变换就行:
令,其中
,考虑到
是对角阵,所以有
,进而有:
,
所有我们的优化目标变成了:
可以发现,这个式子和 RatioCut 基本一致,只是中间的变成了
。同样我们求出来
的 k 个最小的特征值和对应的特征向量得到
,然后对
按行进行标准化,最后再进行一次传统聚类(如 K-Means)就可以了。
顺带说一句,这个其实就是拉普拉斯矩阵标准化的最常用的方式,即
5 谱聚类算法优缺点
搬运文章。
- 优点
- 只需要计算数据之间的相似度矩阵,对于处理稀疏数据的聚类很有效,而传统聚类方法 K-Means 等很难做到
- 由于使用了降维,因此在处理高维数据聚类的时候,复杂度更低
- 缺点
- 结果依赖于相似矩阵,不同的相似矩阵得到的聚类效果很可能不同

