Kernel function 核函数

1 Kernel function 核函数概念

核函数与核方法都是 kernel function，当然也叫核技巧（kernel trick）而且是同一概念。在做分类的过程中，我们经常会遇到一些数据是线性不可分的，而将它们投射到高维空间中就是线性可分的了。例如下图中有二维空间中的“+”“-”两种样本，是线性不可分的；将他们投影到三维空间中就是线性可分的了：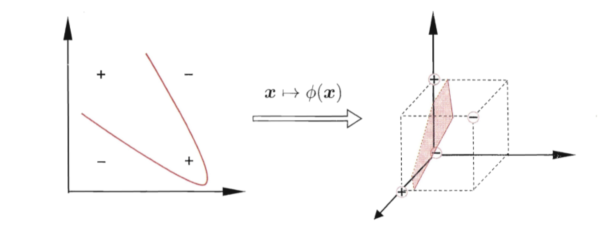

图取自 周志华《机器学习》

还有一个更直观的图，取自文章：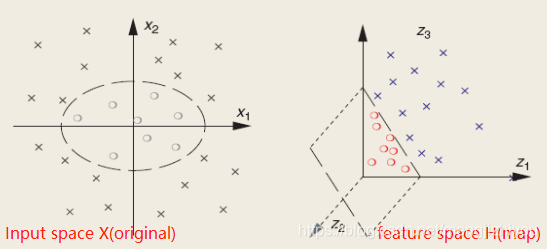

将低维的点映射到高维的映射，我们记作，一般来说。

一般将映射到高维空间得到后，我们就可以对两个点进行运算，例如内积运算：

但通常使用高维数据计算，就不可避免地提高计算的复杂度。为了避免这一复杂度，核函数给出了一种解决方法。设想一个函数，使得

毕竟不管两个点是多少维的，它们的内积都是一个常数。就是希望直接通过对两个低维的点进行某种运算得到一个值，用这个值来代替它们在高维表示中的内积。有了这样的函数，我们就不需要计算高维甚至是无穷维特征空间中的内积了。

这种思想很朴素，也很易懂。因此也能看出，核函数的选择是至关重要的。常用的核函数有：

• 线性核函数

• 高斯核函数（RBF），使用最广泛。能够将原始特征映射到无穷维。

关于推导，见下一章节

• 多项式核函数，可以将原始特征从维映射到维

• tanh 双曲正切函数，主要用于神经网络

2 高斯核函数的理解

高斯核函数又称径向基函数 radial basis function (RBF)，理论上可以将特征空间映射到无穷维，推导如下。

假设，有

通过泰勒公式展开有：

其中

3 参考文章

1. 核函数（kernel function）
2. 核函数（kernel function）