我们来继续上一篇博客中对Java中数组的解读,
我们先来回顾一下
感兴趣的小伙伴可以进去看看哦👉数组(一)
数组(一)中我们解读到了数组的应用场景
那么这篇博客主要针对数组的一些练习和运用以及二维数组进行解析
数组练习
数组转化为字符串
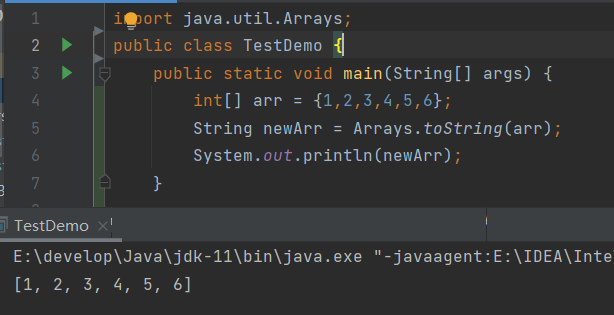
使用这个我们以后打印数组就会更加方便一点。
Java中提供了java.util.Arrays包,其中包含了一些操作数组的常用方法。
这里给大家列举几个常用的方法
1、二叉搜索算法
使用二叉搜索算法搜索指定值的指定数组的范围。在进行此呼叫之前,范围必须按照sort(int[], int, int)方法进行排序。如果没有排序,结果是未定义的。如果范围包含具有指定值的多个元素,则不能保证将找到哪个元素。
2、复制数组内容(下面我还会再提到)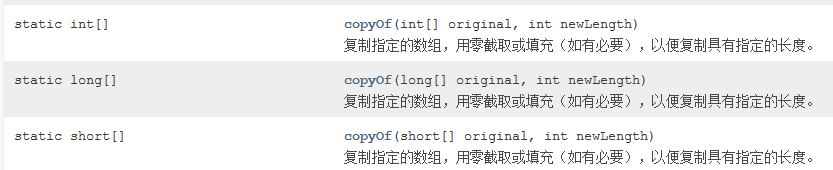
复制指定的数组,用零截取或填充(如有必要),以便复制具有指定的长度。对于原始数组和副本都有效的所有索引,两个数组将包含相同的值。对于在副本中而不是原件有效的任何索引,副本将包含0 。当且仅当指定长度大于原始数组的长度时,这些索引才会存在。
3、数组深度比较
- 返回指定数组的内容的字符串表示形式。 如果数组包含其它数组作为元件,它们被转换为字符串Object.toString()从Object继承的方法,其描述了他们的身份 ,而不是其内容。
- 返回指定数组的“深度内容”的字符串表示形式。
//如果数组包含其他数组作为元素,则字符串表示包含其内容等等。//此方法用于将多维数组转换为字符串。//字符串表示由数组元素的列表组成,括在方括号( "[]" )中。//相邻的元素由字符", " (逗号后跟一个空格)分隔开。//元件由String.valueOf(Object)转换为字符串,除非它们本身阵列。//如果一个元素e是一个基本类型的阵列,它通过调用的Arrays.toString(e)适当重载转换为字符串作为。//如果元素e是引用类型的数组,则通过递归调用此方法将其转换为字符串。//为了避免无限递归,如果指定的数组包含自身作为元素,或者通过一个或多个数组级别包含对其自身的间接引用,则将自引用转换为字符串"[...]" 。//例如,仅包含对其自身的引用的数组将被呈现为"[[...]]" 。//如果指定数组是null此方法返回"null"。
4、按照数组顺序排序
按照数字顺序排列数组的指定范围。要排序的范围从索引fromIndex (包括)扩展到索引toIndex 。如果fromIndex == toIndex ,要排序的范围是空的。
a - 要排序的数组
fromIndex - 要排序的第一个元素的索引(包括)
toIndex - 最后一个要排序的元素的索引
4、equals比较和fill填充
这里用代码来解释
public static void main_ArrayEqualsAndFill(String[] args) {int[] array1 = {1,2,3,4,5};int[] array2 = {1,2,3,4,5};boolean equal = Arrays.equals(array1,array2);System.out.println(equal);System.out.println("==============");int[] array = new int[10];System.out.println("填充之前的数组"+Arrays.toString(array));// 结果都是0Arrays.fill(array,1);System.out.println("填充之后的数组"+Arrays.toString(array));// 结果都是1Arrays.fill(array,4,10,29);// 从[4,10)填充29}
其他的我就不多做介绍了,小伙伴们可以自己去了解一下~
这里我们其实就可以发现了,重载函数真的很常见!
数组的拷贝
这里我们用代码来进行讲解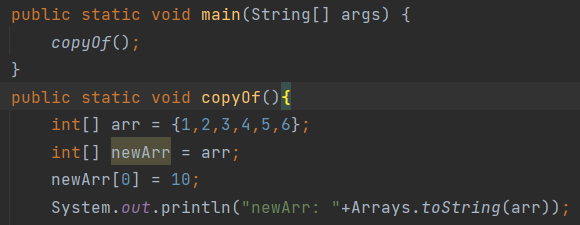
运行结果👇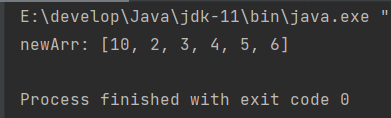
这里newArr和arr引用的是同一个数组,因此newArr修改空间中内容之后,arr也可以看到修改的结果

运行结果👇
使用Arrays中copyOf方法完成对数组的拷贝:
copyOf方法在进行数组拷贝时,创建了一个新的数组
arr和newArr引用的不是同一个数组
因为arr修改其引用数组中内容时,对newArr没有任何影响
运行结果👇
newArr2:[3,4]
这里有一点要注意的是,从2下标拷贝到4下标,都是左闭右开的,不要搞错[2,4)
这个copyOfRange方法看起来很方便呀!让我们瞧瞧得用CTRL+左键来管中窥豹一下源码吧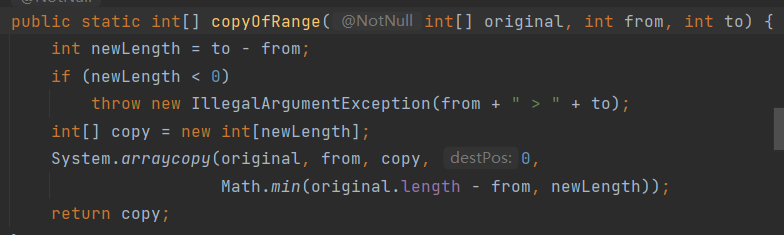
啊,就这么短短几行!而且一眼看过去就可以清楚每行代码的用途,简单干练。
果然还是那句话,最好的代码不是生涩难懂的,而是大家都能看得明白的!
这里我简单画个图来帮大家理解一下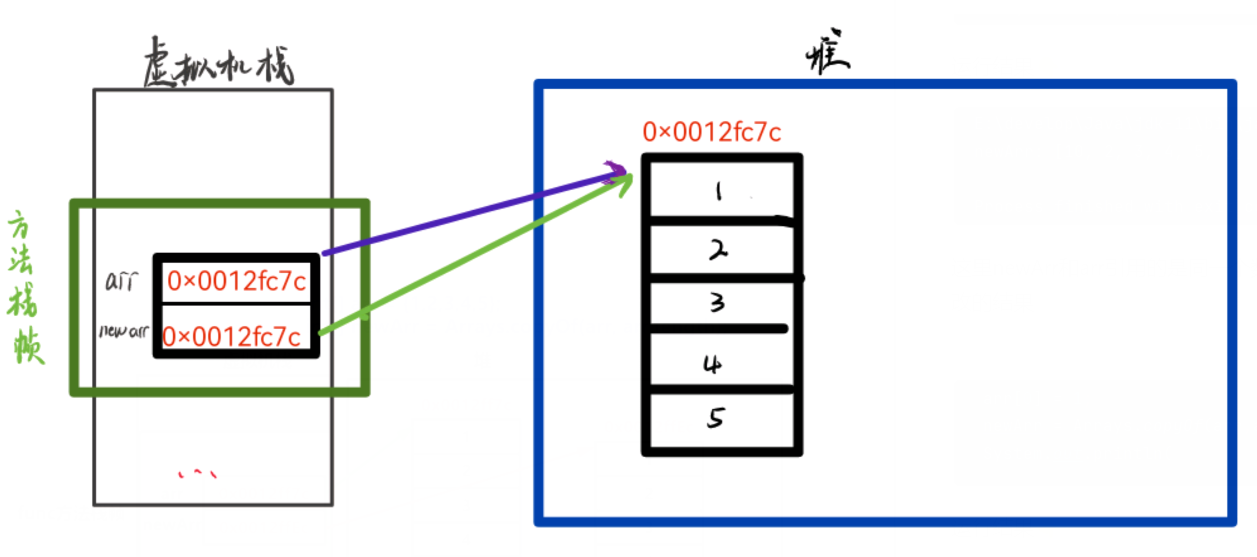
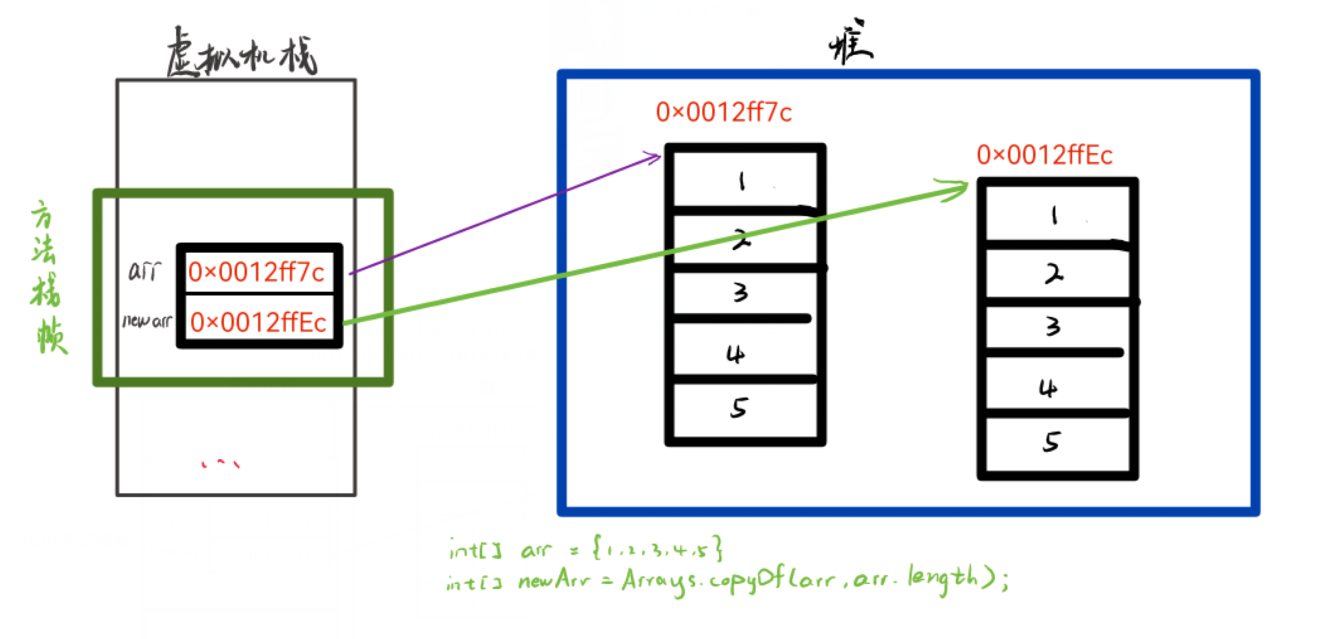
我们在这里要注意的是:数组当中存储的是基本类型数据的时候,不论怎么拷贝基本都不会出现什么问题,但如果存储的是引用数据类型,拷贝的时候就需要考虑深浅拷贝的问题,Arrays中也有相关deepCopyOf等方法,这里待我将数据结构学习透彻再为大家讲解
除了用Java提供的方法,我们当然也可以运用自己写的拷贝数组的方法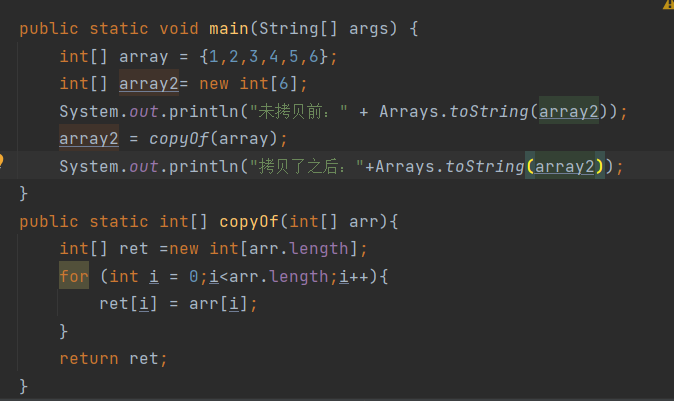
运行结果👇
求数组中元素的平均值
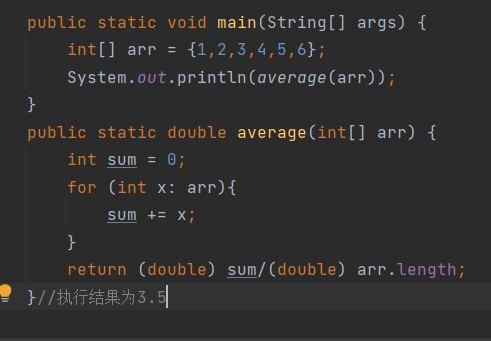
// 求平均值public static double avg(int[] array) {int sum = 0;for (int i = 0;i<array.length;i++){sum = sum +array[i];}return sum*1.0/array.length;// 不能 return sum/array.length}
查找数组中指定元素(顺序查找)
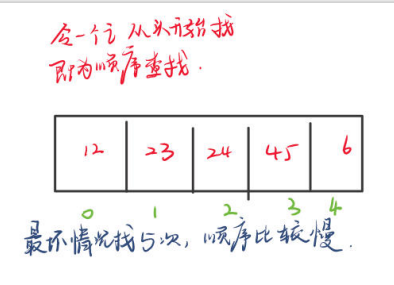
public static int search(int[] array,int key){for(int i=0;i<array.length;i++){if(array[i]==key){return i;}}// 如果代码走到这里,说明推出了for循环return -1;//因为数组没有负数下标}public static void main_search(String[] args) {int[] array = {1,2,3,4,5};int index = search(array,4);if(index == -1){System.out.println("没有你要找的关键字!");}else {System.out.println("找到了你要的关键字,下标是:"+ index);}}
查找数组中指定元素(二分查找)
针对有序数组我们可以进行更加快速的二分查找,一定要注意,是有序!也就是说二分查找的前提是数组是排好序的,千万不要因为这个小细节犯错哦。
而有序数组分为升序和降序,1234为升序,4321为降序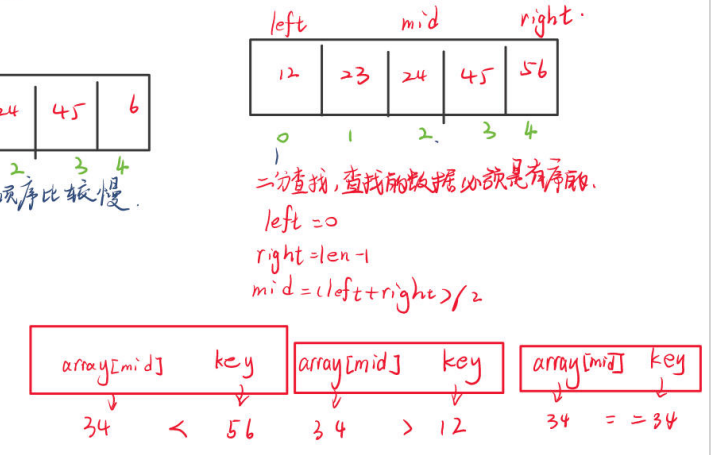
以升序数组为例,二分查找的思路是先取中间位置的元素,然后使用待查找元素与数组中间元素进行比较:
- 如果相等的话,即找到了返回元素在数组中的下标
- 如果小于,以类似方法到数组左半侧进行查找
如果大于,以类似方法到数组右半侧进行查找
// 二分查找,前提是查找的数组有序public static int binarySearch(int[] array,int key){int left = 0;int right = array.length-1;while (left<=right){int mid = (left + right) /2;if (array[mid]<key){left = mid + 1;}else if(array[mid]==key){return mid;}else {right = mid -1;}}// 代码走到这里说明left已经大于right了,所以返回-1return -1;//数组没有-1}
可以看到,针对一个很多元素的数组查找,二分查找的效率极其高,随着数组元素个数越多,那么二分的优势就越大
Arrays中的sort排序方法

(字好丑小伙伴们谅解一下~)
我们用代码来演示一下
这里的sort会自动为我们排序,但它是默认升序的,那么我们再来见识一下源码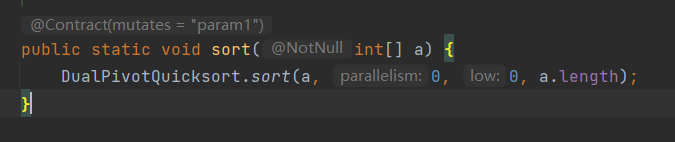
!这又是一个方法,哼哼我再点进去看看 ```java /**- This class implements powerful and fully optimized versions, both
- sequential and parallel, of the Dual-Pivot Quicksort algorithm by
- Vladimir Yaroslavskiy, Jon Bentley and Josh Bloch. This algorithm
- offers O(n log(n)) performance on all data sets, and is typically
- faster than traditional (one-pivot) Quicksort implementations. *
- There are also additional algorithms, invoked from the Dual-Pivot
- Quicksort, such as mixed insertion sort, merging of runs and heap
- sort, counting sort and parallel merge sort. *
- @author Vladimir Yaroslavskiy
- @author Jon Bentley
- @author Josh Bloch
- @author Doug Lea *
- @version 2018.08.18 *
@since 1.7 14 / final class DualPivotQuicksort {
/**
- Prevents instantiation. */ private DualPivotQuicksort() {}
/**
- Max array size to use mixed insertion sort. */ private static final int MAX_MIXED_INSERTION_SORT_SIZE = 65;
/**
- Max array size to use insertion sort. */ private static final int MAX_INSERTION_SORT_SIZE = 44;
/**
- Min array size to perform sorting in parallel. */ private static final int MIN_PARALLEL_SORT_SIZE = 4 << 10;
/**
- Min array size to try merging of runs. */ private static final int MIN_TRY_MERGE_SIZE = 4 << 10;
/**
- Min size of the first run to continue with scanning. */ private static final int MIN_FIRST_RUN_SIZE = 16;
/**
- Min factor for the first runs to continue scanning. */ private static final int MIN_FIRST_RUNS_FACTOR = 7;
/**
- Max capacity of the index array for tracking runs. */ private static final int MAX_RUN_CAPACITY = 5 << 10;
/**
- Min number of runs, required by parallel merging. */ private static final int MIN_RUN_COUNT = 4;
/**
- Min array size to use parallel merging of parts. */ private static final int MIN_PARALLEL_MERGE_PARTS_SIZE = 4 << 10;
/**
- Min size of a byte array to use counting sort. */ private static final int MIN_BYTE_COUNTING_SORT_SIZE = 64;
/**
- Min size of a short or char array to use counting sort. */ private static final int MIN_SHORT_OR_CHAR_COUNTING_SORT_SIZE = 1750;
/**
- Threshold of mixed insertion sort is incremented by this value. */ private static final int DELTA = 3 << 1;
/**
- Max recursive partitioning depth before using heap sort. / private static final int MAX_RECURSION_DEPTH = 64 DELTA;
/**
- Calculates the double depth of parallel merging.
- Depth is negative, if tasks split before sorting. *
- @param parallelism the parallelism level
- @param size the target size
@return the depth of parallel merging */ private static int getDepth(int parallelism, int size) { int depth = 0;
while ((parallelism >>= 3) > 0 && (size >>= 2) > 0) {
depth -= 2;
} return depth; }
/**
- Sorts the specified range of the array using parallel merge
- sort and/or Dual-Pivot Quicksort. *
- To balance the faster splitting and parallelism of merge sort
- with the faster element partitioning of Quicksort, ranges are
- subdivided in tiers such that, if there is enough parallelism,
- the four-way parallel merge is started, still ensuring enough
- parallelism to process the partitions. *
- @param a the array to be sorted
- @param parallelism the parallelism level
- @param low the index of the first element, inclusive, to be sorted
@param high the index of the last element, exclusive, to be sorted */ static void sort(int[] a, int parallelism, int low, int high) { int size = high - low;
if (parallelism > 1 && size > MIN_PARALLEL_SORT_SIZE) {
int depth = getDepth(parallelism, size >> 12);int[] b = depth == 0 ? null : new int[size];new Sorter(null, a, b, low, size, low, depth).invoke();
} else {
sort(null, a, 0, low, high);
} }
/**
- Sorts the specified array using the Dual-Pivot Quicksort and/or
- other sorts in special-cases, possibly with parallel partitions. *
- @param sorter parallel context
- @param a the array to be sorted
- @param bits the combination of recursion depth and bit flag, where
- the right bit “0” indicates that array is the leftmost part
- @param low the index of the first element, inclusive, to be sorted
@param high the index of the last element, exclusive, to be sorted */ static void sort(Sorter sorter, int[] a, int bits, int low, int high) { while (true) {
int end = high - 1, size = high - low;/** Run mixed insertion sort on small non-leftmost parts.*/if (size < MAX_MIXED_INSERTION_SORT_SIZE + bits && (bits & 1) > 0) {mixedInsertionSort(a, low, high - 3 * ((size >> 5) << 3), high);return;}/** Invoke insertion sort on small leftmost part.*/if (size < MAX_INSERTION_SORT_SIZE) {insertionSort(a, low, high);return;}/** Check if the whole array or large non-leftmost* parts are nearly sorted and then merge runs.*/if ((bits == 0 || size > MIN_TRY_MERGE_SIZE && (bits & 1) > 0)&& tryMergeRuns(sorter, a, low, size)) {return;}/** Switch to heap sort if execution* time is becoming quadratic.*/if ((bits += DELTA) > MAX_RECURSION_DEPTH) {heapSort(a, low, high);return;}/** Use an inexpensive approximation of the golden ratio* to select five sample elements and determine pivots.*/int step = (size >> 3) * 3 + 3;/** Five elements around (and including) the central element* will be used for pivot selection as described below. The* unequal choice of spacing these elements was empirically* determined to work well on a wide variety of inputs.*/int e1 = low + step;int e5 = end - step;int e3 = (e1 + e5) >>> 1;int e2 = (e1 + e3) >>> 1;int e4 = (e3 + e5) >>> 1;int a3 = a[e3];/** Sort these elements in place by the combination* of 4-element sorting network and insertion sort.** 5 ------o-----------o------------* | |* 4 ------|-----o-----o-----o------* | | |* 2 ------o-----|-----o-----o------* | |* 1 ------------o-----o------------*/if (a[e5] < a[e2]) { int t = a[e5]; a[e5] = a[e2]; a[e2] = t; }if (a[e4] < a[e1]) { int t = a[e4]; a[e4] = a[e1]; a[e1] = t; }if (a[e5] < a[e4]) { int t = a[e5]; a[e5] = a[e4]; a[e4] = t; }if (a[e2] < a[e1]) { int t = a[e2]; a[e2] = a[e1]; a[e1] = t; }if (a[e4] < a[e2]) { int t = a[e4]; a[e4] = a[e2]; a[e2] = t; }if (a3 < a[e2]) {if (a3 < a[e1]) {a[e3] = a[e2]; a[e2] = a[e1]; a[e1] = a3;} else {a[e3] = a[e2]; a[e2] = a3;}} else if (a3 > a[e4]) {if (a3 > a[e5]) {a[e3] = a[e4]; a[e4] = a[e5]; a[e5] = a3;} else {a[e3] = a[e4]; a[e4] = a3;}}// Pointersint lower = low; // The index of the last element of the left partint upper = end; // The index of the first element of the right part/** Partitioning with 2 pivots in case of different elements.*/if (a[e1] < a[e2] && a[e2] < a[e3] && a[e3] < a[e4] && a[e4] < a[e5]) {/** Use the first and fifth of the five sorted elements as* the pivots. These values are inexpensive approximation* of tertiles. Note, that pivot1 < pivot2.*/int pivot1 = a[e1];int pivot2 = a[e5];/** The first and the last elements to be sorted are moved* to the locations formerly occupied by the pivots. When* partitioning is completed, the pivots are swapped back* into their final positions, and excluded from the next* subsequent sorting.*/a[e1] = a[lower];a[e5] = a[upper];/** Skip elements, which are less or greater than the pivots.*/while (a[++lower] < pivot1);while (a[--upper] > pivot2);/** Backward 3-interval partitioning** left part central part right part* +------------------------------------------------------------+* | < pivot1 | ? | pivot1 <= && <= pivot2 | > pivot2 |* +------------------------------------------------------------+* ^ ^ ^* | | |* lower k upper** Invariants:** all in (low, lower] < pivot1* pivot1 <= all in (k, upper) <= pivot2* all in [upper, end) > pivot2** Pointer k is the last index of ?-part*/for (int unused = --lower, k = ++upper; --k > lower; ) {int ak = a[k];if (ak < pivot1) { // Move a[k] to the left sidewhile (lower < k) {if (a[++lower] >= pivot1) {if (a[lower] > pivot2) {a[k] = a[--upper];a[upper] = a[lower];} else {a[k] = a[lower];}a[lower] = ak;break;}}} else if (ak > pivot2) { // Move a[k] to the right sidea[k] = a[--upper];a[upper] = ak;}}/** Swap the pivots into their final positions.*/a[low] = a[lower]; a[lower] = pivot1;a[end] = a[upper]; a[upper] = pivot2;/** Sort non-left parts recursively (possibly in parallel),* excluding known pivots.*/if (size > MIN_PARALLEL_SORT_SIZE && sorter != null) {sorter.forkSorter(bits | 1, lower + 1, upper);sorter.forkSorter(bits | 1, upper + 1, high);} else {sort(sorter, a, bits | 1, lower + 1, upper);sort(sorter, a, bits | 1, upper + 1, high);}} else { // Use single pivot in case of many equal elements/** Use the third of the five sorted elements as the pivot.* This value is inexpensive approximation of the median.*/int pivot = a[e3];/** The first element to be sorted is moved to the* location formerly occupied by the pivot. After* completion of partitioning the pivot is swapped* back into its final position, and excluded from* the next subsequent sorting.*/a[e3] = a[lower];/** Traditional 3-way (Dutch National Flag) partitioning** left part central part right part* +------------------------------------------------------+* | < pivot | ? | == pivot | > pivot |* +------------------------------------------------------+* ^ ^ ^* | | |* lower k upper** Invariants:** all in (low, lower] < pivot* all in (k, upper) == pivot* all in [upper, end] > pivot** Pointer k is the last index of ?-part*/for (int k = ++upper; --k > lower; ) {int ak = a[k];if (ak != pivot) {a[k] = pivot;if (ak < pivot) { // Move a[k] to the left sidewhile (a[++lower] < pivot);if (a[lower] > pivot) {a[--upper] = a[lower];}a[lower] = ak;} else { // ak > pivot - Move a[k] to the right sidea[--upper] = ak;}}}/** Swap the pivot into its final position.*/a[low] = a[lower]; a[lower] = pivot;/** Sort the right part (possibly in parallel), excluding* known pivot. All elements from the central part are* equal and therefore already sorted.*/if (size > MIN_PARALLEL_SORT_SIZE && sorter != null) {sorter.forkSorter(bits | 1, upper, high);} else {sort(sorter, a, bits | 1, upper, high);}}high = lower; // Iterate along the left part
} }
/**
- Sorts the specified range of the array using mixed insertion sort. *
- Mixed insertion sort is combination of simple insertion sort,
- pin insertion sort and pair insertion sort. *
- In the context of Dual-Pivot Quicksort, the pivot element
- from the left part plays the role of sentinel, because it
- is less than any elements from the given part. Therefore,
- expensive check of the left range can be skipped on each
- iteration unless it is the leftmost call. *
- @param a the array to be sorted
- @param low the index of the first element, inclusive, to be sorted
- @param end the index of the last element for simple insertion sort
@param high the index of the last element, exclusive, to be sorted */ private static void mixedInsertionSort(int[] a, int low, int end, int high) { if (end == high) {
/** Invoke simple insertion sort on tiny array.*/for (int i; ++low < end; ) {int ai = a[i = low];while (ai < a[--i]) {a[i + 1] = a[i];}a[i + 1] = ai;}
} else {
/** Start with pin insertion sort on small part.** Pin insertion sort is extended simple insertion sort.* The main idea of this sort is to put elements larger* than an element called pin to the end of array (the* proper area for such elements). It avoids expensive* movements of these elements through the whole array.*/int pin = a[end];for (int i, p = high; ++low < end; ) {int ai = a[i = low];if (ai < a[i - 1]) { // Small element/** Insert small element into sorted part.*/a[i] = a[--i];while (ai < a[--i]) {a[i + 1] = a[i];}a[i + 1] = ai;} else if (p > i && ai > pin) { // Large element/** Find element smaller than pin.*/while (a[--p] > pin);/** Swap it with large element.*/if (p > i) {ai = a[p];a[p] = a[i];}/** Insert small element into sorted part.*/while (ai < a[--i]) {a[i + 1] = a[i];}a[i + 1] = ai;}}/** Continue with pair insertion sort on remain part.*/for (int i; low < high; ++low) {int a1 = a[i = low], a2 = a[++low];/** Insert two elements per iteration: at first, insert the* larger element and then insert the smaller element, but* from the position where the larger element was inserted.*/if (a1 > a2) {while (a1 < a[--i]) {a[i + 2] = a[i];}a[++i + 1] = a1;while (a2 < a[--i]) {a[i + 1] = a[i];}a[i + 1] = a2;} else if (a1 < a[i - 1]) {while (a2 < a[--i]) {a[i + 2] = a[i];}a[++i + 1] = a2;while (a1 < a[--i]) {a[i + 1] = a[i];}a[i + 1] = a1;}}
} }
....好家伙,见识不过来了,等有空我再为大家去庖丁解牛(鸽王发言)<a name="iX5zn"></a>## 数组排序(冒泡排序)<br />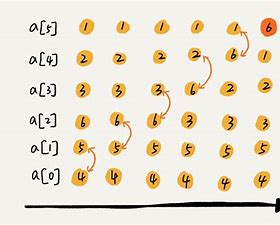<br />假设我们需要对数组进行升序排序1. 将数组中相邻元素从前往后依次进行比较,如果前一个元素比后一个元素大,则交换,一趟下来之后最大的元素就在数组的末尾1. 依次从上述过程,知道数组中所有的元素都排列好```javapublic static void bubbleSort(int[] array) {//[0----len-1)i代表趟数for (int i = 0;i<array.length-1;i++){boolean flg = false;//j<4在这里可以不减i 减i说明是进行了优化for(int j=0;j<array.length-1-i;j++){if (array[j] > array[j+1]) {int tmp = array[j];array[j] = array[j+1];array[j+1] = tmp;flg = true;}}if (flg == false) {// 这里是判断上一次有没有进行交换,flg有没有变成truebreak;}}// 这里还可以进一步优化,我们可以进一步添加检查,// 检查是否发生了简化,如果没有,说明有序了,就不需要进行第三趟,第四趟...}

冒泡排序相对Arrays提供的sort性能还是欠佳,所以还是多多利用Arrays提供的方法咯
数组逆序
我们给定一个数组,然后将里面的元素逆序排列
思路如下: 设定两个下标,分别指向第一个和最后一个元素,减缓两个位置的元素 然后让前一个下标自增,后一个下标自减,循环继续即可
public static void reverse(int[] arr) {int left = 0;int right = arr.length-1;int tmp = 0;while (left<right){tmp = arr[left];arr[right] = tmp;left++;right--;}
二维数组
基本语法
数据类型[][] 数组名称 = new 数据类型 [行数][列数] {初始化数据};
介绍几种初始化方式
import java.util.ArrayList;public class TestDemo{public static void main(String args[]) {int[][]a1= {{1,2},{3,4},{5,6,7}};for(int i=0;i<a1.length;i++) {System.out.print(a1[i].length+" ");for(int j=0;j<a1[i].length;j++)System.out.print(a1[i][j]+" ");System.out.println();}System.out.println();int[][]a2=new int[2][3];for(int i=0;i<a2.length;i++) {System.out.print(a2[i].length+" ");for(int j=0;j<a2[i].length;j++)System.out.print(a2[i][j]+" ");System.out.println();}System.out.println();int[][]a3=new int[2][];for(int i=0;i<a3.length;i++) {a3[i]=new int[3];System.out.print(a3[i].length+" ");for(int j=0;j<a3[i].length;j++)System.out.print(a3[i][j]+" ");System.out.println();}System.out.println();ArrayList<Integer> a4[]=new ArrayList[3];for(int i=0;i<a4.length;i++) {a4[i]=new ArrayList();a4[i].add(1);for(int j:a4[i])System.out.print(j+" ");System.out.println();}}}
输出👇
2 1 22 3 43 5 6 73 0 0 03 0 0 03 0 0 03 0 0 0111
二维数组的用法和一维数组并没有明显的差别,所以不在赘述,除了要注意的是不规则数组的情况,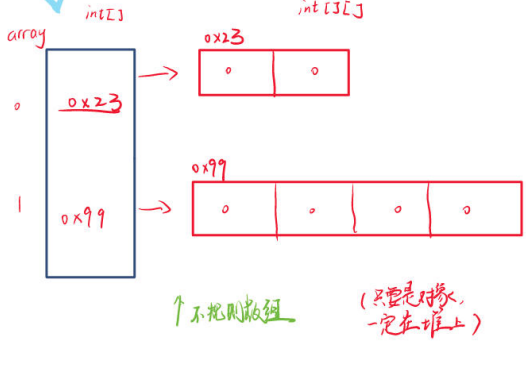
这里我给出一段代码,来帮助大家理解
public static void main_3(String[] args) {int[] arr = {1,2,3,4,5,6};String newArr = Arrays.toString(arr);System.out.println(newArr);}public static void main_2(String[] args) {// int[][] array = {{1,2},{4,5,6}};是可以这样定义的int[][] array2=new int[2][];//这里编译器只知道这里有两行,还没给出列array2[0] = new int[2];array2[1] = new int[4];// 这叫不规则数组for (int i = 0;i<array2.length;i++){//代表我们的行for (int j =0;j<array2[i].length;j++){//代表我们的列System.out.println(array2[i][j]);}}// 这里没有array2[0] = new int[2];// array2[1] = new int[4];// 会显示空指针异常,// PS:这里区别于C语言,不能再使用array+1来表示数组地址了}public static void main_1(String[] args){// 二维数组不能这么写 int[][] array = {1,2,3,4,5,6};int[][] array = {{1,2,3},{4,5,6}};int[][] array2 = new int [][]{{1,2,3},{4,5,6}};for (int i = 0;i<2;i++){//代表我们的行for (int j =0;j<3;j++){//代表我们的列System.out.println(array[i][j]);}}// 优化一下for (int i = 0;i<array.length;i++){//代表我们的行for (int j =0;j<array[i].length;j++){//代表我们的列System.out.println(array[i][j]);}}System.out.println("使用for-each来进行打印");for (int[] tmp:array){for(int x:tmp){System.out.println(x+" ");}}System.out.println("使用toString进行打印");System.out.println(Arrays.deepToString(array));//}

