🐳 1. 时间复杂度

🦐 1.1时间复杂度的概念

时间复杂度就是用来方便开发者估算出程序的运行时间

我们该如何估计程序运行时间呢，我们通常会估计算法的操作单元数量，来代表程序消耗的时间， 这里我们默认CPU的每个单元运行消耗的时间都是相同的。

假设算法的问题规模为n，那么操作单元数量便用函数f(n)来表示

随着数据规模n的增大，算法执行时间的增长率和f(n)的增长率相同，这称作为算法的渐近时间复杂度，简称时间复杂度，记为 O(f(n))

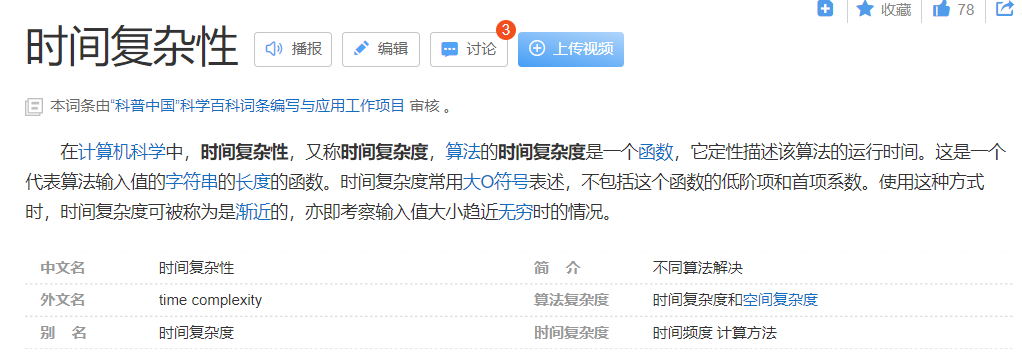
image.png

判断一个算法所编程序运行时间的多少，并不是将程序编写出来，通过在计算机上运行所消耗的时间来度量。原因很简单，一方面，解决一个问题的算法可能有很多种，一一实现的工作量无疑是巨大的，得不偿失；另一方面，不同计算机的软、硬件环境不同，即便使用同一台计算机，不同时间段其系统环境也不相同，程序的运行时间很可能会受影响，严重时甚至会导致误判。 实际场景中，我们更喜欢用一个估值来表示算法所编程序的运行时间。所谓估值，即估计的、并不准确的值。注意，虽然估值无法准确的表示算法所编程序的运行时间，但它的得来并非凭空揣测，需要经过缜密的计算后才能得出。 也就是说，表示一个算法所编程序运行时间的多少，用的并不是准确值（事实上也无法得出），而是根据合理方法得到的预估值。 那么，如何预估一个算法所编程序的运行时间呢？很简单，先分别计算程序中每条语句的执行次数，然后用总的执行次数间接表示程序的运行时间。

🦑 1.2怎么计算时间复杂度

  1. 🦜 1.2.1找出基本语句

在一段代码中，循环执行最多次数的就是基本语句
比如下面代码中

  1. public class Test1 {
  2.     public static void main(String[] args) {
  3.         int i,j=0;
  4.         Scanner scanner = new Scanner(System.in);
  5.         String str = scanner.next();
  6.         char[] ch = str.toCharArray();
  7.         char[] ch1 = new char[ch.length];
  8.         ch1[0]=ch[0];
  9.         //这里的是双重for循环，代码循环执行次数最多，为基本语句
  10.         for(i=1;i<str.length();i++){
  11.             int k =0;
  12.             for (int n = 0; n <= j; n++){
  13.                 if (ch[i]==ch1[j]){
  14.                     break;
  15.                 }
  16.                  k=1;
  17.             }
  18.             if (k==0){
  19.                 continue;
  20.             }else{
  21.                 j++;
  22.                 ch1[j]=ch[i];
  23.             }
  24.         }
  25.         boolean sort = false;
  26.         //我们可以看到这里有个双重for循环，也是基本语句
  27.         for (int a = 0;a<Math.sqrt(ch1.length);a++){
  29.             for (int b = 1;b<ch1.length-1;b++) {
  30.                 if (ch1[b - 1] > ch1[b]) {
  31.                     int temp = ch1[b - 1];
  32.                     ch1[b - 1] = ch1[b];
  33.                     ch1[b] = (char) temp;
  34.                 } else if (b == ch1.length - 1) {
  35.                     sort = true;
  36.                 }
  37.             }
  38.             if (sort == true){
  39.                 break;
  40.             }
  41.         }
  42.         System.out.println(ch1);
  43.     }
  44. }

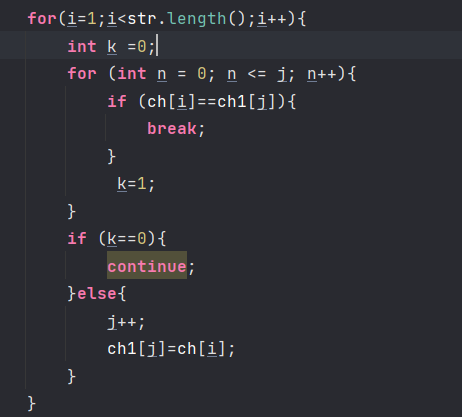
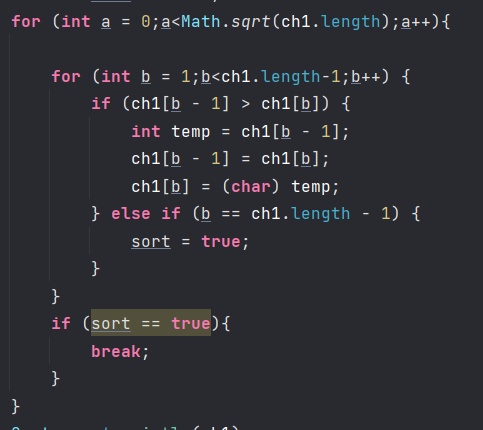
image.png
image.png
那么我们可以看到有两个双重for循环，两个基本语句，我们要选择哪一条作为基本语句呢？

  1. 🦩 计算基本语句中，执行次数的数量级

    那么根据我们上面的例子， 第一个for循环的数量级为str.length()j 第二个for循环的数量级为Math.sqrt(ch1.length)ch1.length-1 那么第一个我们可以当作为nn=n² 第二个我们可以当作n(n-1)=n²-n

  2. 🦚 用O()来计算算法的时间性能，即时间复杂度

什么是大O呢？

算法导论给出的解释：大O用来表示上界的，当用它作为算法的最坏情况运行时间的上界，就是对任意数据输入的运行时间的上界。

我们将n²和n²-n放入O()中，那么保留最高次幂
最后剩下的都是n²，所以它们的时间复杂度都是n²

常见的算法时间复杂度由小到大依次为： Ο(1)＜Ο(log2n)＜Ο(n)＜Ο(nlog2n)＜Ο(n²)＜Ο(n³)＜…＜Ο(2^n)＜Ο(n!)<O(n^n) image.png 用函数图像能更容易理解

🐙 1.3代码示例判断时间复杂度

🐿️ 1.3.1示例1

  1.     public static String func(String str){
  2.         int[] array1 = new int[127];
  3.         StringBuilder sb = new StringBuilder();
  4.         for (int i = 0;i<str.length();i++){
  5.             char ch = str.charAt(i);
  6.             if (array1[ch]==0){
  7.                 sb.append(ch);
  8.                 array1[ch]=1;
  9.             }
  10.         }
  11.         str = sb.toString();
  12.         return str;
  13.     }

这里只有一个for循环，我们将它作为基本语句，循环次数为str.length()，看作n，它的时间复杂度即为O(N)

🦫 1.3.2 示例2

  1. // 这是一个二分查找的方法
  2. public int binarySearch(int[] array, int value) {
  3.     int begin = 0;
  4.     int end = array.length - 1;
  5.     while (begin <= end) {
  6.         int mid = begin + ((end-begin) / 2);
  7.         if (array[mid] < value){
  8.             begin = mid + 1;
  9.         }else if (array[mid] > value){
  10.             end = mid - 1;
  11.         }else{
  12.             return mid;
  13.         }
  14.     }
  15.     return -1;
  16. }

二分查找有个很重要的特点，就是不会查找数列的全部元素，而查找的数据量其实正好符合元素的对数，正常情况下每次查找的元素都在一半一半地减少。 所以二分查找的 时间复杂度 为 O (log 2 n) 是毫无疑问的。 当然，最好的情况是只查找一次就能找到，但是在最坏和一般情况下的确要比顺序查找好了很多。 二分查找要求数列本身有序，所以在选择的时候需要确认数列是否本身有序，如果无序，则还需要进行排序，确认这样的代价是否符合实际需求。 其实我们在获取一个列表的很多时候，可以直接使用数据库针对某个字段进行排序，在程序中需要找出某个值的元素时，就很适合使用二分查找了。

那么我们来分析一下二分查找的时间复杂度

总共有n个元素。 第1次折半：还剩n/2个元素 第2次折半：还剩n/4个元素 第3次折半：还剩n/8个元素 …… 第k次折半：还剩n/2^k个元素 最坏的情况下，最后还剩1个元素，令n/2^k = 1。得k=logn。

🥐 2.空间复杂度

image.png

🍞 2.1空间复杂度的概念

和时间复杂度类似，一个算法的空间复杂度，也常用大 O 记法表示。 要知道每一个算法所编写的程序，运行过程中都需要占用大小不等的存储空间，例如： 程序代码本身所占用的存储空间；程序中如果需要输入输出数据，也会占用一定的存储空间；程序在运行过程中，可能还需要临时申请更多的存储空间。 首先，程序自身所占用的存储空间取决于其包含的代码量，如果要压缩这部分存储空间，就要求我们在实现功能的同时，尽可能编写足够短的代码。 程序运行过程中输入输出的数据，往往由要解决的问题而定，即便所用算法不同，程序输入输出所占用的存储空间也是相近的。事实上，对算法的空间复杂度影响最大的，往往是程序运行过程中所申请的临时存储空间。不同的算法所编写出的程序，其运行时申请的临时存储空间通常会有较大不同。

总而言之，空间复杂度是对一个算法在运行过程中占用内存空间大小的量度

🥖 2.2怎么计算空间复杂度

  1. int j = 0;
  2. for (int i = 0; i < n; i++) {
  3.     j++;
  4. }

我们可以看到代码中有个循环，每次循环都会创建一个i。
但是这里的空间复杂度实际上并不为n，因为此处j开辟了一个常量内存，i虽然循环n次开辟了n次内存，但是它的每次循环结束后之前开辟的都会“释放”（具体可能是被JVM的垃圾回收机制处理了），所以这里实际上i还是开辟了一个常量的内存，我们将i和j的常量内存加起来，还是个常量，放入O()中化简为1，那么这个代码的空间复杂度即为O(1).

🥨 2.3代码示例判断空间复杂度

🐇 2.3.1示例1

  1. public void function() {
  2.     int a[] = { 1, 2, 3, 4, 5 };
  3.     int tmp = 0;
  4.     for (int i = 0; i < (a.length / 2); i++) {
  5.         tmp = a[i];
  6.         a[i] = a[a.length - i - 1];
  7.         a[a.length - i - 1] = tmp;
  8.     }
  9.     System.out.println(Arrays.toString(a));
  10. }

这是一段很具有迷惑性的代码，虽然看上去有for循环也定义了一个a数组，但是我们再仔细看看代码中都是常量定义的，所以这段代码的空间复杂度实则为O(1).

🦖 2.3.2 示例2

  1. //这是一个冒泡排序   
  2. public void bubbleSort(int[] array) {
  3.         for (int end = array.length; end > 0; end--) {
  4.             boolean sorted = true;
  5.             for (int i = 1; i < end; i++) {
  6.                 if (array[i - 1] > array[i]) {
  7.                     Swap(array, i - 1, i);
  8.                     sorted = false;
  9.                 }
  10.             }
  11.             if (sorted == true) {
  12.                 break;
  13.             }
  14.         }
  15.     }

冒泡排序的辅助变量空间仅仅是一个临时变量，并且不会随着排序规模的扩大而进行改变，所以空间复杂度为O (1)。 因为排序中始终只用到了数组大小的空间，为常数，因此空间复杂度为O (1)。 在一个数组中，找一个数为基准数，将这个数中所有比基准数大的数放在该数的右边，比基准数小的数放在该数的左边。当最后平分的不能再平分时，也就是说把公式一直往下跌倒，到最后得到T [1]时，说明这个公式已经迭代完了（T [1]是常量了）。

有完善补充的请dd我哦
感谢阅读~