一、什么是递归？

自身不断地循环自身。
最简单的递归：
计算阶乘n! = 1 * 2 * 3 * 4 * …… * (n-1) * n
循环实现：

  1. public static int factorial(int n) {
  2.     int factorial = 1;
  3.     for (int i = 1; i <= n; i++) {
  4.         factorial *= i;
  5.     }
  6.     return factorial;
  7. }

递归实现：

  1. public static int factorial(int n) {
  2.     //#1. 当 n = 1 时，递归结束
  3.     if (n == 1) {
  4.         return 1;
  5.     }
  6.     //#2. 把 factorial(n - 1) 的结果和 n 相乘，剩下的交给 factorial(n - 1) 来解决。
  7.     return n * factorial(n - 1);
  8. }

二、如何实现递归？

1.基准条件（结束条件，没有这个条件代码将出现死循环）
2.递归公式（递归公式总是描述自己和下一个递归函数直接的递进关系）
image.png
练习题1.
image.png

答案：

  1. package com.youkeda;
  3. public class Recursive {
  5.   public static int fibonacci(int n) {
  6.         if (n == 0 || n == 1) {
  7.       return n;
  8.     }
  9.     return fibonacci(n - 1) + fibonacci(n - 2);
  10.       }
  12.   public static void main(String[] args) {
  13.     System.out.println("fibonacci(1) = " + fibonacci(1));
  14.     System.out.println("fibonacci(3) = " + fibonacci(3));
  15.     System.out.println("fibonacci(10) = " + fibonacci(10));
  16.   }
  17. }

练习题2
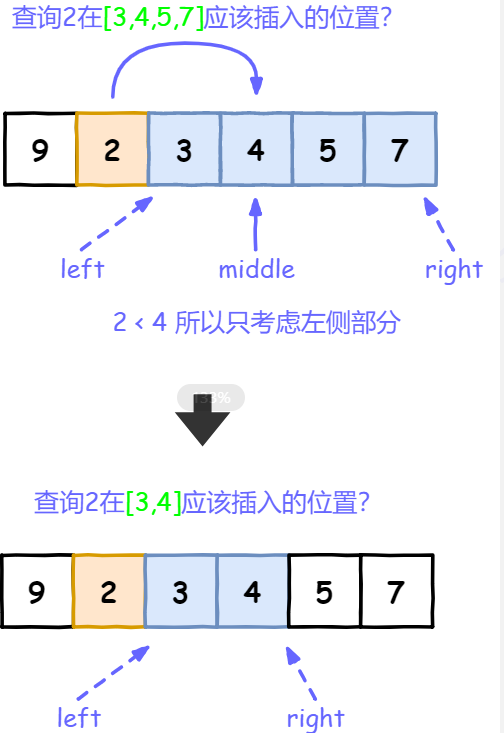
image.png
image.png

答案：

  1. package com.youkeda;
  3. import java.util.Arrays;
  4. public class Recursive {
  5.   // 查找应该插入的索引位置
  6.   public static int searchIndex(int[] array, int left, int right, int aim) {
  7.     // 循环查找节点位置
  8.     if (left < right) {
  9.       int middle = (left + right) / 2;
  10.       int value = array[middle];
  11.       if (value < aim) {
  12. //        left = middle + 1;
  13.         return searchIndex(array, middle + 1, right, aim);
  14.       } else {
  15. //        right = middle - 1;
  16.           return searchIndex(array, left, right-1, aim);
  17.       }
  18.     }
  19.     // #1. 如果最终元素仍然大于目标元素，则将索引位置往左边移动一个
  20.     if (array[left] > aim) {
  21.       return left - 1;
  22.     }
  23.     // 否则就是当前位置
  24.     return left;
  25.   }
  27.   // 插入排序
  28.   public static void insertSort(int[] array) {
  29.     // 从倒数第二位开始，遍历到底0位，遍历 N-1 次
  30.     for (int i = array.length - 2; i >= 0; i--) {
  31.       // 存储当前抽离的元素
  32.       int temp = array[i];
  33.       //获取应该插入的索引位置
  34.       int index = searchIndex(array, i + 1, array.length - 1, temp);
  36.       // 根据插入的索引位置，进行数组的移动和插入
  37.       int j = i + 1;
  38.       //对数组进行移动
  39.       while (j <= index) {
  40.         array[j - 1] = array[j];
  41.         j++;
  42.       }
  43.       //给数组末尾赋值
  44.       array[j - 1] = temp;
  45.     }
  46.   }
  47.   public static void main(String[] args) {
  48.     int[] array = {9, 2, 4, 7, 5, 3};
  49.     // Arrays.toString 可以方便打印数组内容
  50.     System.out.println(Arrays.toString(array));
  51.     insertSort(array);
  52.     System.out.println(Arrays.toString(array));
  53.   }
  54. }

三、分而治之思想-归并排序

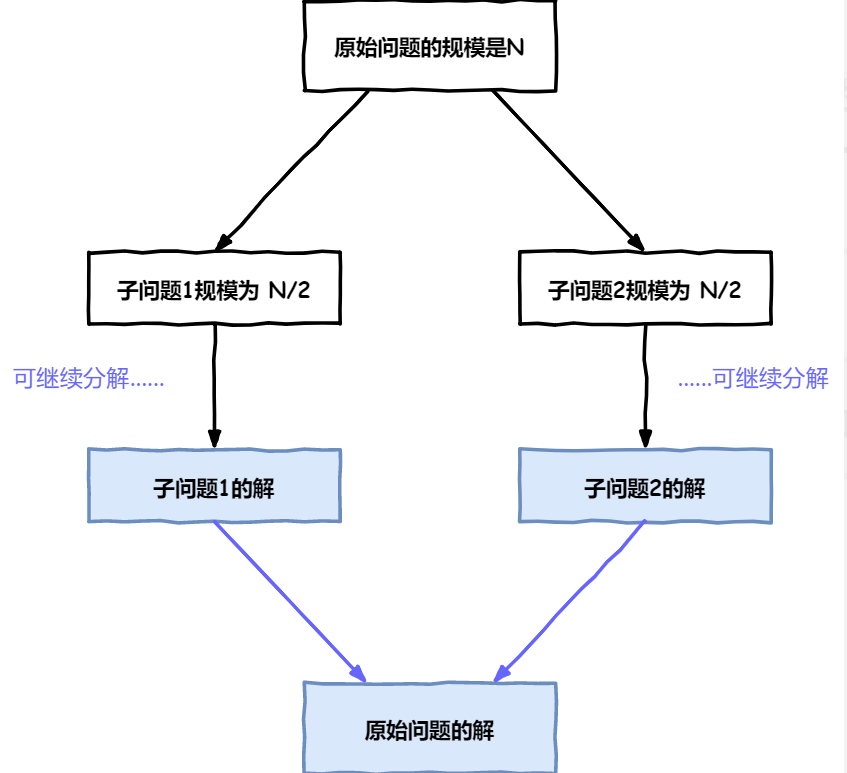
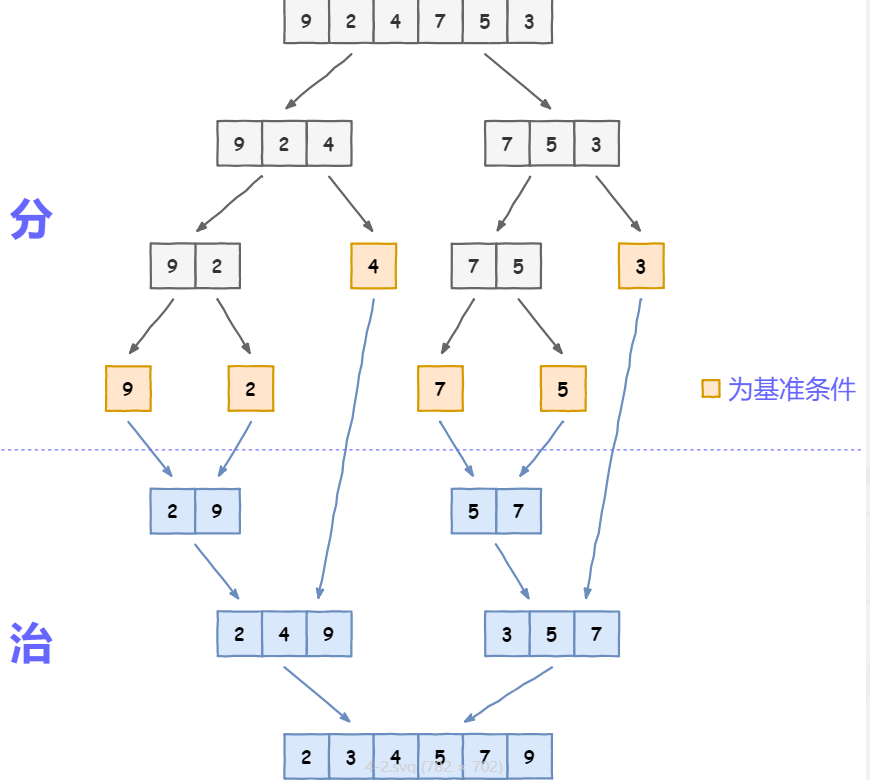
image.pngimage.pngimage.pngimage.png
image.pngimage.pngimage.png

  1. // 归并排序，返回排好序的数组
  2. public static int[] mergeSort(int[] array) {
  3.     // 为了方便查看结果，我们将每个数组进行打印
  4.     System.out.println(Arrays.toString(array));
  5.     if (array.length == 1) {
  6.         return array;
  7.     }
  9.     int middle = array.length / 2;
  10.     // #1. 处理 0 到 middle 左侧数组部分
  11.     int[] left = mergeSort(subArray(array, 0, middle));
  12.     // #2. 处理 middle 到 array.length 右侧数组部分
  13.     int[] right = mergeSort(subArray(array, middle, array.length));
  15.     // TODO处理合并问题
  16.     return array;
  17. }

大家重点理解上面#1 #2注释的代码，理解创建子数组，然后递归分治的逻辑（我们暂时忽略合并排序的逻辑）。
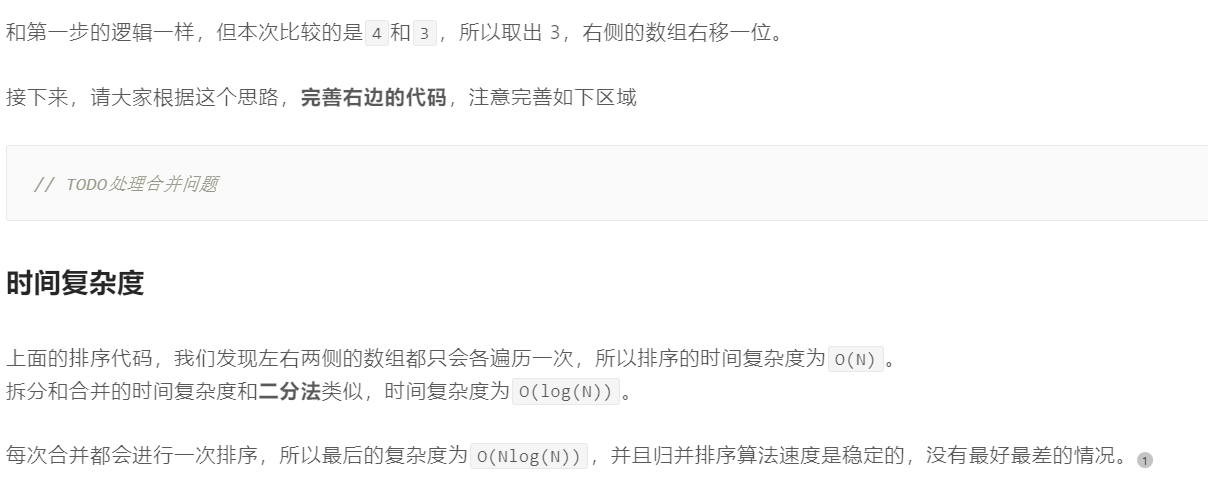
image.png
image.png
递归 - 图14
image.png递归 - 图16
image.png递归 - 图18image.png
代码实现：

  1. package com.youkeda;
  3. import java.util.Arrays;
  5. public class Sort {
  7.   // 归并排序
  8.   public static int[] mergeSort(int[] array) {
  9.     // 为了方便查看结果，我们将每个数组进行打印
  10.     if (array.length == 1) {
  11.       return array;
  12.     }
  14.     int middle = array.length / 2;
  15.     // 处理 0 到 middle 左侧数组部分
  16.     int[] left = mergeSort(subArray(array, 0, middle));
  17.     // 处理 middle 到 array.length 右侧数组部分
  18.     int[] right = mergeSort(subArray(array, middle, array.length));
  20.     // TODO处理合并问题
  21.      int l = 0;
  22.     int r = 0;
  23.     int index = 0;
  24.     // 依次比较左右两个数组
  25.     while (l < left.length && r < right.length) {
  26.       array[index] = Math.min(left[l], right[r]);
  27.       index++;
  28.       if (left[l] < right[r]) {
  29.         l++;
  30.       } else {
  31.         r++;
  32.       }
  33.     }
  35.     // 右侧数组已经遍历完成，左侧有剩余
  36.     if (l < left.length) {
  37.       for(int i = l; i < left.length; i++){
  38.         array[index] = left[i];
  39.         index++;
  40.       }
  41.     }
  43.     // 左侧数组已经遍历完成，右侧有剩余
  44.     if(r < right.length){
  45.       for(int i = r; i < right.length; i++){
  46.         array[index] = right[i];
  47.         index++;
  48.       }
  49.     }
  51.     return array;
  52.   }
  53.   // 拷贝原数组的部分内容，从 left 到 right
  54.   public static int[] subArray(int[] source, int left, int right) {
  55.     // 创建一个新数组
  56.     int[] result = new int[right - left];
  57.     // 依次赋值进去
  58.     for (int i = left; i < right; i++) {
  59.       result[i - left] = source[i];
  60.     }
  61.     return result;
  62.   }
  64.   public static void main(String[] args) {
  65.     int[] array = {9, 2, 4, 7, 5, 3};
  66.     // Arrays.toString 可以方便打印数组内容
  67.     System.out.println("raw: " + Arrays.toString(array));
  68.     int[] result = mergeSort(array);
  69.     System.out.println("result: " + Arrays.toString(result));
  70.   }
  71. }

四、分而治之思想-快速排序（重要）

快速排序使用分治法将序列分成两个较大和较小的子序列，然后递归的排序两个子序列。

  1. 挑选基准值：从数列中挑出一个元素，称为“基准”（pivot），
  2. 分割：所有比基准值小的元素放在基准值的左边，所有比基准值大的元素放在基准值的右边，分割成两个子序列
  3. 递归排序子序列：递归地将小于基准值元素的子序列和大于基准值元素的子序列排序。

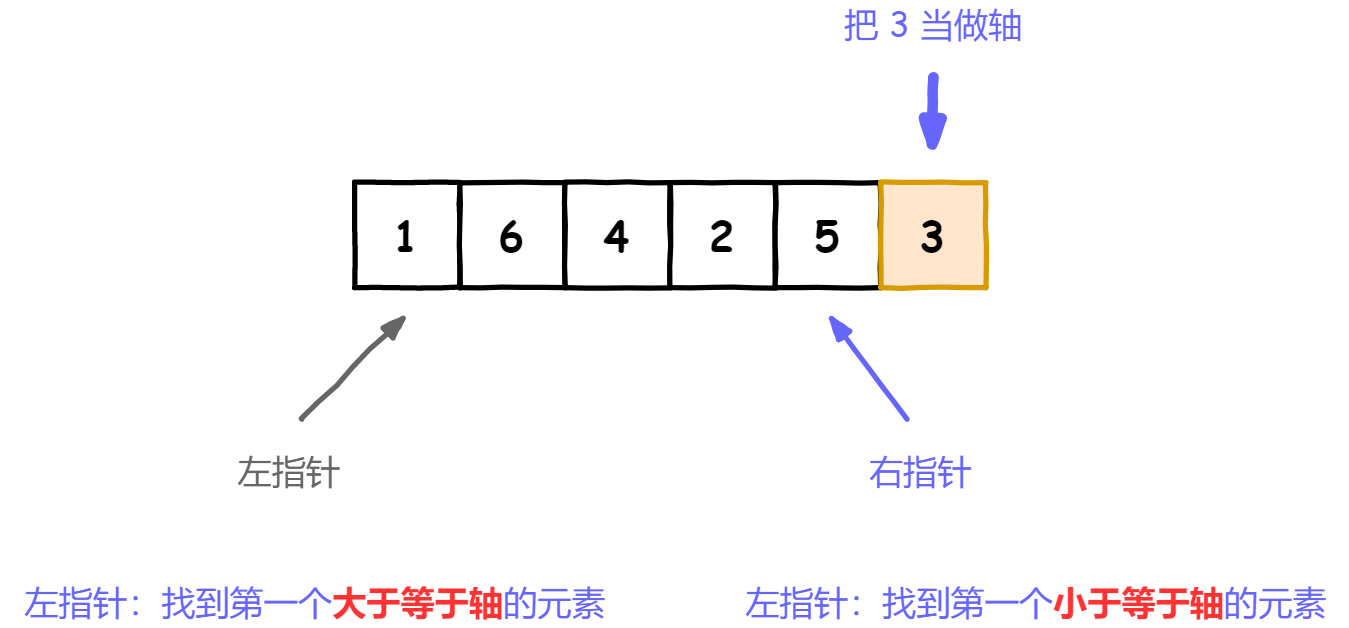
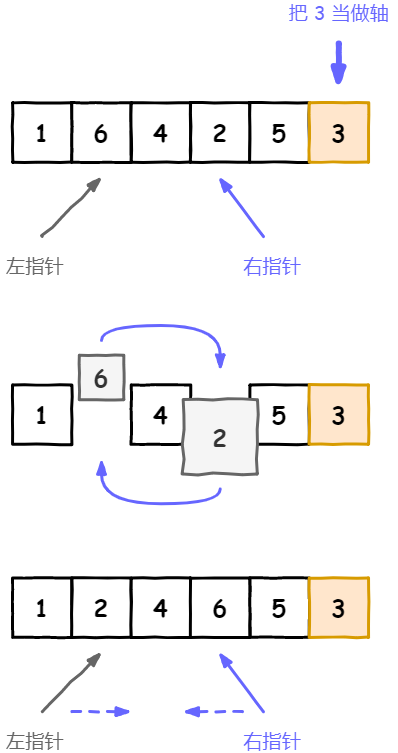
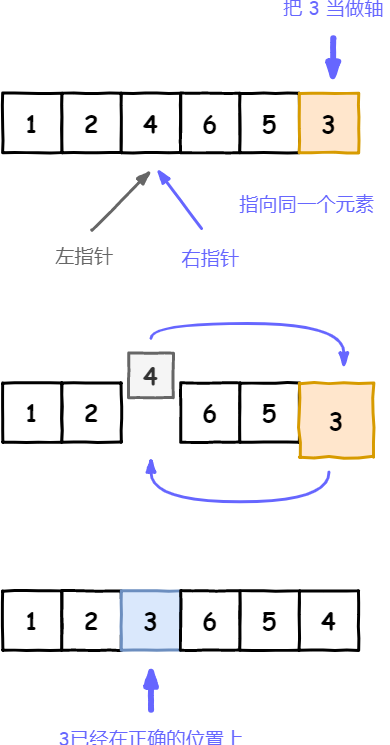
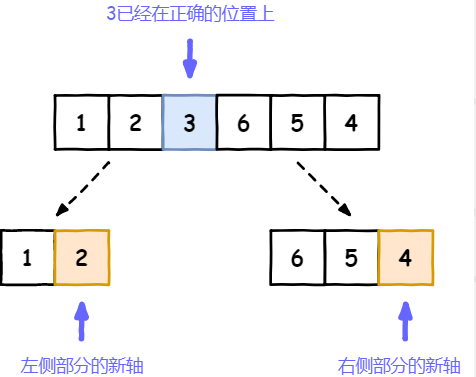
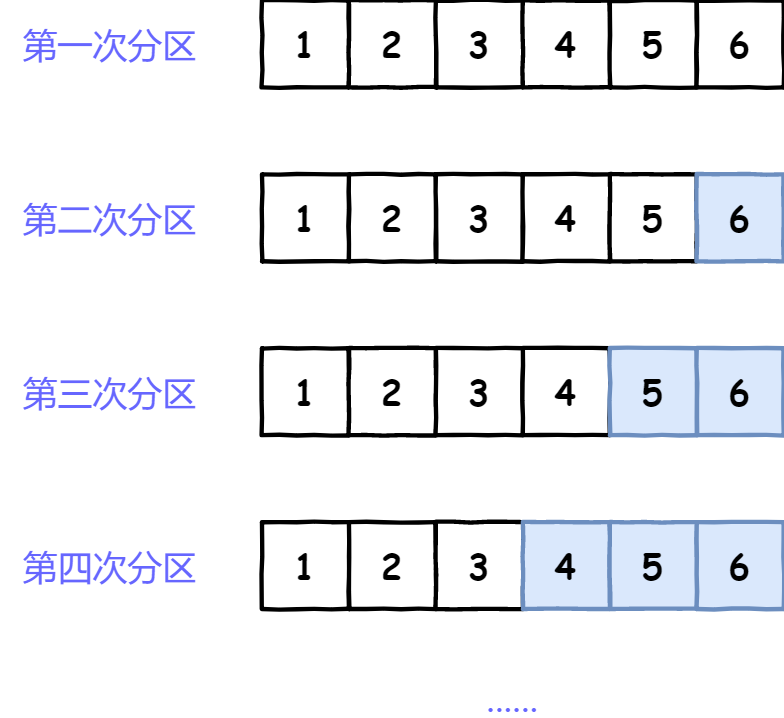
image.png
image.pngimage.png
image.pngimage.pngimage.pngimage.png
image.pngimage.png
image.pngimage.pngimage.pngimage.png

  1. // 快速排序
  2. public static void quickSort(int[] array) {
  3.     // 调用快速排序的核心，传入left，right
  4.     quickSortCore(array, 0, array.length - 1);
  5. }
  7. // 快速排序的核心，同样也是递归函数
  8. public static void quickSortCore(int[] array, int left, int right) {
  9.     // 递归基准条件，left >= right 即表示数组只有1个或者0个元素。
  10.     if (left >= right) {
  11.         return;
  12.     }
  13.     // 根据轴分区
  14.     int pivotIndex = partition(array, left, right);
  16.     // 递归调用左侧和右侧数组分区
  17.     quickSortCore(array, left, pivotIndex - 1);
  18.     quickSortCore(array, pivotIndex + 1, right);
  19. }
  21. // 对数组进行分区，并返回当前轴所在的位置
  22. public static int partition(int[] array, int left, int right) {
  24. }

image.png
答案：

  1. package com.youkeda;
  3. import java.util.Arrays;
  5. public class QuickSort {
  7.   // 快速排序
  8.   public static void quickSort(int[] array) {
  9.     // 调用快速排序的核心，传入left，right
  10.     quickSortCore(array, 0, array.length - 1);
  11.   }
  13.   // 快速排序的核心，同样也是递归函数
  14.   public static void quickSortCore(int[] array, int left, int right) {
  15.     // 递归基准条件，left >= right 即表示数组只有1个或者0个元素。
  16.     if (left >= right) {
  17.       return;
  18.     }
  19.     // 根据轴分区
  20.     int pivotIndex = partition(array, left, right);
  22.     // 递归调用左侧和右侧数组分区
  23.     quickSortCore(array, left, pivotIndex - 1);
  24.     quickSortCore(array, pivotIndex + 1, right);
  25.   }
  27.   // 对数组进行分区，并返回当前轴所在的位置
  28.   public static int partition(int[] array, int left, int right) {
  29.     int pivot = array[right];
  31.     int leftIndex = left;
  32.     int rightIndex = right - 1;
  33.     while (true) {
  34.       // 左指针移动
  35.       while (array[leftIndex] <= pivot && leftIndex < right) {
  36.         leftIndex++;
  37.       }
  38.       // 右指针移动
  39.       while (array[rightIndex] >= pivot && rightIndex > 0) {
  40.         rightIndex--;
  41.       }
  43.       if (leftIndex >= rightIndex) {
  44.         break;
  45.       } else {
  46.         swap(array, leftIndex, rightIndex);
  47.       }
  48.     }
  50.     swap(array, leftIndex, right);
  51.     return leftIndex;
  52.   }
  54.   public static void swap(int[] array, int index1, int index2) {
  55.     int temp = array[index1];
  56.     array[index1] = array[index2];
  57.     array[index2] = temp;
  58.   }
  60.   public static void main(String[] args) {
  61.     int[] array = {9, 2, 4, 7, 5, 3};
  62.     // Arrays.toString 可以方便打印数组内容
  63.     System.out.println("raw: " + Arrays.toString(array));
  64.     quickSort(array);
  65.     System.out.println("result: " + Arrays.toString(array));
  66.   }
  67. }

五、快速排序应用-快速选择

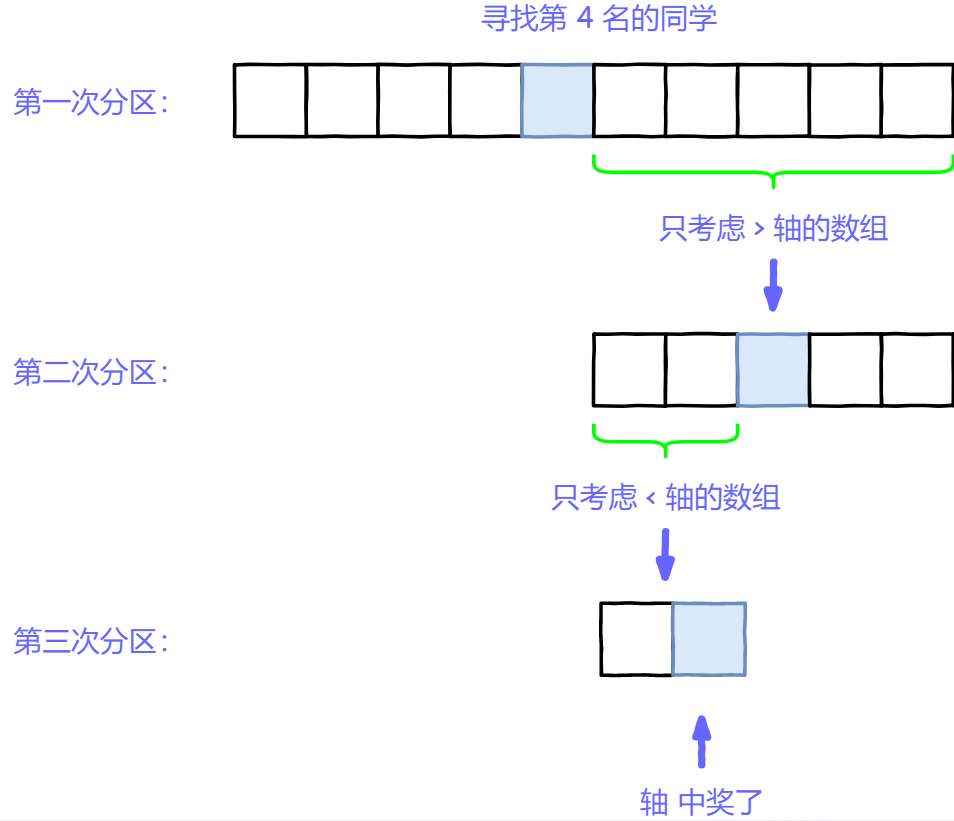
image.pngimage.pngimage.pngimage.png
答案：

  1. package com.youkeda;
  3. import java.util.Arrays;
  5. public class QuickSort {
  7.   // 快速选择，返回选中的元素
  8.   public static int quickFind(int[] array, int aim) {
  9.     // 调用快速选择的核心，传入left，right
  10.     return quickFindCore(array, aim, 0, array.length - 1);
  11.   }
  13.   // 快速选择的核心，同样也是递归函数
  14.   public static int quickFindCore(int[] array, int aim, int left, int right) {
  15.     // 递归基准条件，left >= right 即表示数组只有1个或者0个元素，返回当前的元素
  16.     if (left >= right) {
  17.       return array[left];
  18.     }
  19.     // 根据轴分区
  20.     int pivotIndex = partition(array, left, right);
  21.     // 根据 aim 确定继续递归的方向
  22.     if (pivotIndex > aim) {
  23.       return quickFindCore(array, aim, left, pivotIndex - 1);
  24.     } else if (pivotIndex < aim) {
  25.       return quickFindCore(array, aim, pivotIndex + 1, right);
  26.     } else {
  27.       return array[pivotIndex];
  28.     }
  29.   }
  31.   // 对数组进行分区，并返回当前轴所在的位置
  32.   public static int partition(int[] array, int left, int right) {
  33.     int pivot = array[right];
  35.     int leftIndex = left;
  36.     int rightIndex = right - 1;
  37.     while (true) {
  38.       // 左指针移动
  39.       while (array[leftIndex] < pivot && leftIndex < right) {
  40.         leftIndex++;
  41.       }
  42.       // 右指针移动
  43.       while (array[rightIndex] > pivot && rightIndex > 0) {
  44.         rightIndex--;
  45.       }
  47.       if (leftIndex >= rightIndex) {
  48.         break;
  49.       } else {
  50.         swap(array, leftIndex, rightIndex);
  51.       }
  52.     }
  54.     swap(array, leftIndex, right);
  55.     return leftIndex;
  56.   }
  58.   public static void swap(int[] array, int index1, int index2) {
  59.     int temp = array[index1];
  60.     array[index1] = array[index2];
  61.     array[index2] = temp;
  62.   }
  64.   public static void main(String[] args) {
  65.     int[] array = {72, 77, 48, 17, 71, 2, 25, 97, 82, 5, 2, 18, 15, 57, 7, 48, 93, 47, 38, 74, 18, 93, 98, 41, 54, 4, 47, 4, 63, 76};
  66.     System.out.println("raw: " + Arrays.toString(array));
  67.     // 目标是倒数第 6 个元素
  68.     int result = quickFind(array, array.length - 6);
  69.     System.out.println("result: " + result);
  70.   }
  71. }