一、动态规划Dynamic Programming

什么是动态规划？

动态规划算法通常基于一个递推公式及一个或多个初始状态。 当前子问题的解将由上一次子问题的解推出。使用动态规划来解题只需要多项式时间复杂度， 因此它比回溯法、暴力法等要快许多。

Overlap sub-problem问题

即重叠子问题。
先引入Fibonacci Sequence。斐波那契数列：1 1 2 3 5 8 13 ...
公式：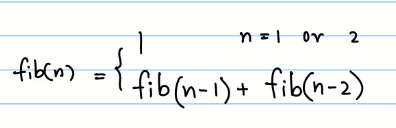
image.png
举例：如果计算fib(6)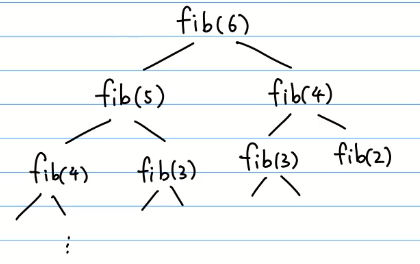
image.png
按照公式，把fib(6)拆分成fib(5)和fib(4),在计算fib(5)的时候又会计算fib(4)，这对计算机而言就是很浪费资源的一件事，时间复杂度能达到O(2)，这就是重叠子问题。

解决方案：
当fib(4)计算出来后，把它临时存在数组里，下次再想要fib(4)结果值的时候，不必再重新计算fib(3)和fib(2)，直接从临时数组里取值就好，时间复杂度降到O（n)，这样效率就加大了很多。

动态规划入门题

最大工资问题

问题描述：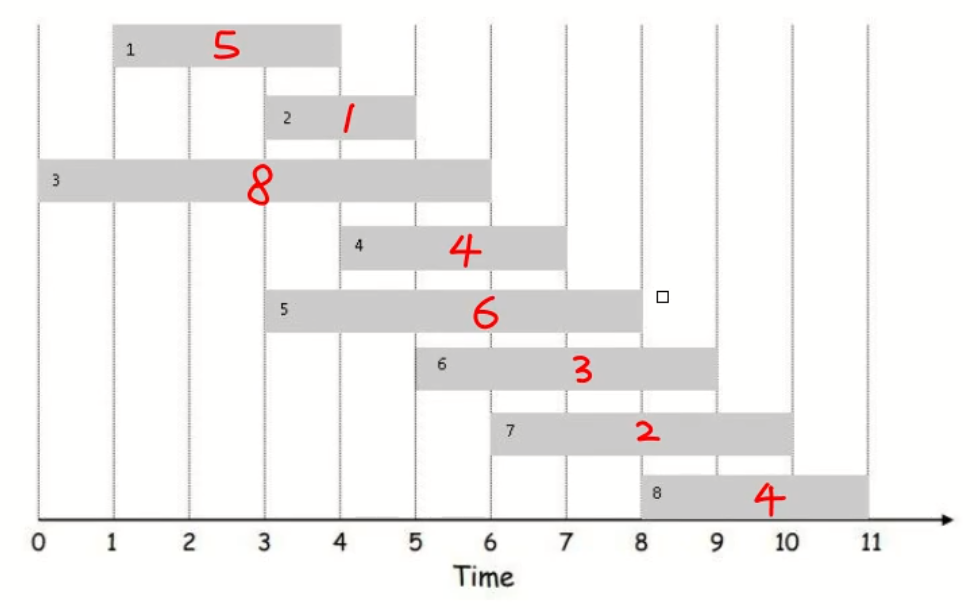
image.png
横轴代表时间，方块内的黑色序号为任务标号，红色数字代表在该工时内所能得到的薪资，如果两个工时有冲突，则不能同时接领任务，否则可以接领多个任务，求在该图时间内能得到的最大薪资是多少？

例如：

如果选择了第8个任务，就不能选择第6、7个，但可以选择第5个（不冲突），如果选择了第5个，前四个都不能选了，如果不选第5个，可以选择第3个，薪资为8，此时为最优解。

分析：

对于这类题目，有一个非常好的方法，叫做选和不选。
设OPT（optimal的缩写）为选择任务的最优解，那么OPT(i)，当i=1,2,3,4,…8时，该任务的最优解是什么。

举例：当考虑第8个任务的时候，需要思考选第8个任务和不选择第8个任务会产生什么样的效果？

选择第8个任务首先能赚4块钱，然后考虑选择8之后还能选择哪个离8最近的任务，然后再递归考虑该任务是选还是不选。（这里为什么要选择离8最近呢？是为了能够适配递归方法，从最近的任务里判断选则它之后能达到最优解还是不选择它之后能达到最优解）

如果不选择第8个，那就从剩下7个中选出最优解，直接递归考虑第7个选还是不选。

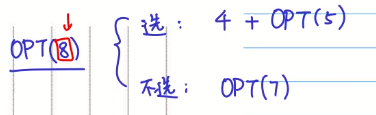image.png通式==image.png

此时OPT（8）会有选和不选两种状态的值，再考虑。

列表分析：

image.png

i(任务序号) prev(i)（非要做第i个任务的话前面会最近能做哪个任务） OPT（i）（最优解的值）
1 0 5（选第一个任务，i=1）
2 0 5（不选第二个任务，i=1）
3 0 8（i=3）
4 1 9（i=1，4）
5 0 9（i=1，4）
6 2 9（i=1，4）
7 3 10（i=3，7）
8 5 13（i=5，8 = 1，4，8）

image.png

代码实现：

从一组数字中选出非相邻数字的最大值

问题描述：给定一组数字，要求从这组数字里找出非 相邻数字和的最大值。

举例：

输入：4 1 1 9 1

输出：13（9+4）

输入：1 2 4 1 7 8 3

输出：15 （3+7+4+1）

分析：

image.png

设OPT（6）为一组数字下标为6的位置最佳方案，V（6）为下标是6的值

还是老套路，选和不选，谁选和不选？分析下标为6位置的数字是选还是不选

如果选择下标6，则不能选下标5，状态转移方程为OPT（4）+V（6）

如果不选下标6，状态转移方程为OPT（5）

此时就又可以递归处理OPT（5）和OPT（4）

寻找递归出口：

如果只有一个数字的话：OPT（0）= V（0）；

如果有两个数字的话：OPT（1）= Max（V（0），V（1））；

代码实现：

  1. public class Demo {
  2.     //递归实现
  3.     public static int rec_opt(int[] arr, int i) {
  4.         if (i == 0)
  5.             return arr[0];
  6.         else if (i == 1)
  7.             return arr[0] > arr[1] ? arr[0] : arr[1];
  8.         else {
  9.             int a = rec_opt(arr, i - 2) + arr[i];
  10.             int b = rec_opt(arr, i - 1);
  11.             return a > b ? a : b;
  12.         }
  13.     }
  14.     //动态规划实现
  15.     public static int dp_opt(int[] arr,int x) {
  16.         int[] opt = new int[arr.length];
  17.         opt[0] = arr[0];
  18.         opt[1] = arr[0] > arr[1] ? arr[0] : arr[1];
  19.         for (int i = 2; i < opt.length; i++) {
  20.             int a = opt[i - 2] + arr[i];
  21.             int b = opt[i - 1];
  22.             opt[i] = a > b ? a : b;
  23.         }
  24.         return opt[x];
  25.     }
  26.     //测试
  27.     public static void main(String[] args) {
  28.         int[] arr = { 4, 1, 1, 9, 1 };
  29.         System.out.println(dp_opt(arr,arr.length - 1));
  30.         System.out.println(rec_opt(arr, arr.length - 1));
  31.     }
  32. }

判断一组数字中是否满足几个数字的和为一个指定数字

问题描述：

给定一组数字，判断是否满足里面某几个数字加起来正好等于目标数字。(假设这一组数字都为正数)

举例一：

输入：
arr = { 3 , 34 , 4 , 12 , 5 , 2 }；

S = 9

输出：
true （3+4+2=9）

举例二：
输入：
arr = { 3 , 34 , 4 , 12 , 5 , 2 }；

S = -1

输出：
false

分析：

设Subset(i,s)（SubsetSubset子集，i 表示下标为 i 的数字，s为最终加出来的结果）
例子一：
能满足Subset(arr[5],9)就输出true，否则输出false；arr[5]表示从下标为0到下标为5的数字中，是否含有满足和为9的数字。
而Subset(arr[5],9)又包含两种情况，即arr[5]是选还是不选，如果选，则条件变成Subset(arr[4],7)，如果不选，则条件变成Subset(arr[4],9);只要这两种情况有任意一种能成立，则返回true；

出口：
第一种情况：
在处理的过程中发现s已经等于0，比如Subset(arr[2],0);这种情况直接返回true，下标从0到2的数字不用看了。
第二种情况：
当处理最后一个数字的时候，s还不等于0，这时候必须最后一个数字等于s，比如Subset(arr[0],3),这时判断arr[0]是否等于3，如果等于则返回true，否则返回false；
优化：
如果i大于s，那么此事只能不选i，否则如果选了结果会一直大于s，永远凑不成i，即如果arr[i]>s，return Subset(arr[i-1] , s)

  1. public class Demo {
  3. //递归实现
  4.     public static boolean rec_subset(int[] arr, int i, int s) {
  5.         if (s == 0)
  6.             return true;
  7.         else if (i == 0)
  8.             return arr[0] == s;
  9.         else if (arr[i] > s)
  10.             return rec_subset(arr, i - 1, s);
  11.         else {
  12.             boolean a = rec_subset(arr, i - 1, s - arr[i]);
  13.             boolean b = rec_subset(arr, i - 1, s);
  14.             if (a || b)
  15.                 return true;
  16.         }
  17.         return false;
  19.     }
  20. //动态规划实现
  21.     public static boolean dp_subset(int[] arr, int S) {
  22.         boolean[][] subset = new boolean[arr.length][S + 1];
  23.         for (int i = 0; i < arr.length; i++) {
  24.             subset[i][0] = true;
  25.         }
  26.         for (int i = 0; i < S + 1; i++) {
  27.             subset[0][i] = false;
  28.         }
  29.         if (S >= arr[0]) {
  30.             subset[0][arr[0]] = true;
  31.         }
  32.         for (int i = 1; i < arr.length; i++) {
  33.             for (int s = 1; s < S + 1; s++) {
  34.                 if (arr[i] > s) {
  35.                     subset[i][s] = subset[i - 1][s];
  36.                 } else {
  37.                     boolean a = subset[i - 1][s - arr[i]];
  38.                     boolean b = subset[i - 1][s];
  39.                     subset[i][s] = a || b;
  40.                 }
  41.             }
  42.         }
  43.         return subset[arr.length - 1][S];
  44.     }
  45. }

银行换钱最少硬币问题

问题描述：如果我们有面值为1元、3元和5元的硬币若干枚，如何用最少的硬币凑够11元？
有人会说这太简单，对是太简单，但请你用动态规划解，将问题进行抽象，最后达到什么程度了，给出任意面值集合V，凑够的面值为m,求所需硬币最少的个数 j.

分析：
首先我们思考一个问题，如何用最少的硬币凑够m元，为什么要这么问呢？
两个原因：
1.当我们遇到一个大问题时，总是习惯把问题的规模变小，这样便于分析讨论。
2.这个规模变小后的问题和原来的问题是同质的，除了规模变小，其它的都是一样的， 本质上它还是同一个问题(规模变小后的问题其实是原问题的子问题)。

好了，让我们从最小的m开始吧。

  • 当m=0，即我们需要多少个硬币来凑够0元。 由于1，3，5都大于0，即没有比0小的币值，因此凑够0元我们最少需要0个硬币。 这时候我们发现用一个标记来表示这句“凑够0元我们最少需要0个硬币。”会比较方便， 如果一直用纯文字来表述，不出一会儿你就会觉得很绕了。那么， 我们用d(m)=j来表示凑够m元最少需要j个硬币。于是我们已经得到了d(0)=0， （注意d(0)=0可以做为动态规划的初始状态)，表示凑够0元最小需要0个硬币。
  • 当m=1时，只有面值为1元的硬币可用， 因此我们拿起一个面值为1的硬币，接下来只需要凑够0元即可，而这个是已经知道答案的， 即d(0)=0。所以，d(1)=d(1-1)+1=d(0)+1=0+1=1。
  • 当m=2时， 仍然只有面值为1的硬币可用，于是我拿起一个面值为1的硬币， 接下来我只需要再凑够2-1=1元即可(记得要用最小的硬币数量)，而这个答案也已经知道了。 所以d(2)=d(2-1)+1=d(1)+1=1+1=2。一直到这里，你都可能会觉得，好无聊， 感觉像做小学生的题目似的。因为我们一直都只能操作面值为1的硬币！
  • 耐心点， 让我们看看m=3时的情况。当m=3时，我们能用的硬币就有两种了：1元的和3元的( 5元的仍然没用，因为你需要凑的数目是3元！5元太多了亲)。 既然能用的硬币有两种，我就有两种方案。如果我拿了一个1元的硬币，我的目标就变为了： 凑够3-1=2元需要的最少硬币数量。即d(3)=d(3-1)+1=d(2)+1=2+1=3。 这个方案说的是，我拿3个1元的硬币；第二种方案是我拿起一个3元的硬币， 我的目标就变成：凑够3-3=0元需要的最少硬币数量。即d(3)=d(3-3)+1=d(0)+1=0+1=1. 这个方案说的是，我拿1个3元的硬币。好了，这两种方案哪种更优呢？ 记得我们可是要用最少的硬币数量来凑够3元的。所以， 选择d(3)=1，怎么来的呢？具体是这样得到的：d(3)=min{d(3-1)+1, d(3-3)+1}。min{ }为取集合中的最小值，上面的min{d(3-1)+1,d(3-3)+1} 取最小值为d(3-3)+1。简单的过程分析后，让我们来点抽象的。从以上的文字中， 我们要抽出动态规划里非常重要的两个概念：状态和状态转移方程。

    状态和状态转移方程

    据上文我们可以抽象的d(i) (0<=i<=m)表示凑够i元需要的最少硬币数量，我们将它定义为该问题的”状态”。
    这个状态是怎么找出来的呢？
    它根据子问题定义状态。你找到子问题，状态也就浮出水面了。比如d(11),d(0),d(1)等等这些都是状态 ，这些状态的值我们都要进行保存，以便下一步子问题查阅上一步子问题的解，我们最终的状态是解决问题,所以终态为d(11)，即凑够11元最少需要多少个硬币。
    那状态转移方程是什么呢？
    既然我们用d(i)表示状态，那么状态转移方程自然包含d(i)， 上文中包含状态d(i)的方程是：d(3)=min{d(3-1)+1, d(3-3)+1}。没错， 它就是状态转移方程，描述状态之间是如何转移的。当然，我们要对它抽象一下， d(i)=min{ d(i-vj)+1 }，其中i-vj >=0，vj表示集合V中第j个硬币的面值
    那min{} 是怎么操作的呢？
    以上面的为例，m=11, v={1,3,5} ，d(11)=min{d(11-1)+1,d(11-3)+1,d(11-5)+1}=min{d(10)+1,d(8)+1,d(6)+1};找出里面的最小值，d(10)+1,d(8)+1,d(6)+1,从中可以看出，我们是从底向上解题，也就是说从d(0)开始一直到d(11)。我们将所解的每个状态的值都保存到一个集合中。按这个原则，我们可以得到d(11) ,它所依赖的d(10),d(8),d(9)我们都可以从状态集合中获取。这样我就可以只关心当前状态的求解，而不用关心它之前的状态，因为它之前的状态都是已知的。
    有了状态和状态转移方程，这个问题基本上也就解决了。
    下面我们来看一下代码要怎么实现的：
    1. public class MinCoin{
    2.     public static int dp(int[]V,int m){
    3.         //用于保存状态
    4.         int[] minSV=new int[m+1];
    5.         //初始状态 将d(0)保存到状态集合中
    6.         minSV[0]=0;
    7.         //保证minSV[i]即d(i)只被初始化一次
    8.         boolean flog=true;
    9.         //获取d(1)到的(m)所有的状态值,将其保存到状态集合中
    10.            for(int i=1;i<=m;i++){
    11.                 flog=true;
    12.             for(int j=0;j<V.length;j++){
    13.                 //d(i)=min{d(i-vj)+1}
    14.                 //先假设d(i)为要比较集合min{..}内的第一个。即将d(i)初始化为min{。。}内的第一个。
    15.                if(V[j]<=i && flog){
    16.                   minSV[i]=minSV[i-V[j]]+1;
    17.                   //保证只初始化一次
    18.                   flog=false;
    19.                }
    20.                //获取集合内最小的一个赋值给d(i) 即d(i)=min{d(i-vj)+1}
    21.                //所用选取的面值vj不能大于要凑够的面值i,且的d(i-vj)是min{..}内最小的
    22.                if(V[j]<=i && minSV[i-V[j]]+1<minSV[i]){
    23.                    minSV[i]=minSV[i-V[j]]+1;
    24.                }
    25.             }
    26.         }
    27.         //返回终态d(m)的值
    28.         return minSV[m];
    29.     }
    30.     public static void main(String[] args) {
    31.            //要凑够的面值为11
    32.               int m=11;
    33.             //可用的面值集合为V
    34.              int[] V=new int[]{1,3,5};
    35.            System.out.println("最少需要："+dp(V,m)+"枚硬币");
    36.   }
    37. }

    二、贪心算法