131.分割回文串

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

回文串 是正着读和反着读都一样的字符串。

示例 1： 输入：s = “aab” 输出：[[“a”,”a”,”b”],[“aa”,”b”]] 示例 2： 输入：s = “a” 输出：[[“a”]]

提示： 1 <= s.length <= 16 s 仅由小写英文字母组成

解法1

  • 思路：难点是考虑这个字符串要怎么截取：利用循环i和current，先让i为current，保证被current-1选过的无法再次选取。再通过循环i让每次循环能够截取的长度增大，这样就能得到不同长度的字符串，同时也能保证在同一个集合中题目给出的字符串中每个字符都能出现。并且为了让性能提升需要剪枝，先判断是否为回文串，不是则直接剪枝
  • 流程图

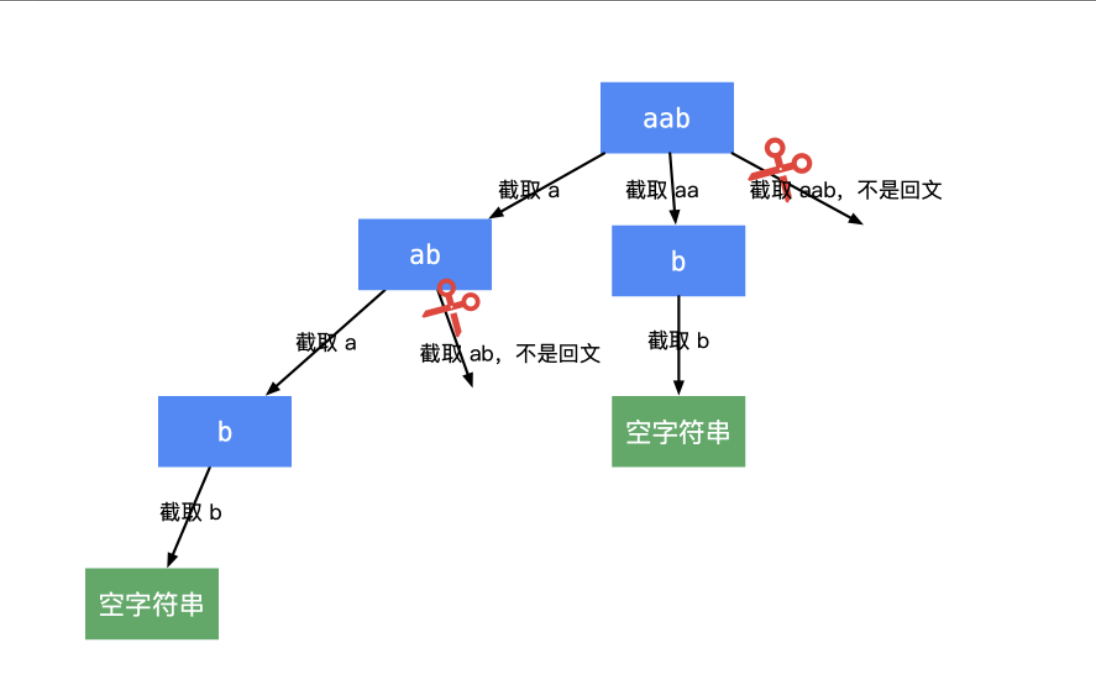
  • image.png

    1.    static List<List<String>> res;
    2.    public static List<List<String>> partition2(String s) {
    3.       res = new ArrayList<>();
    4.       char[] chars = s.toCharArray();
    5.       Deque<String> perm = new ArrayDeque<>();
    6.       dfs(chars, 0, perm);
    7.       return res;
    8.   }
    9.    /**
    10.    * 怎么让截取的长度不一样？
    11.    * 利用i和current，随着循环层数的增加使截取长度的增加。current的增加只是使得开始截取的位置改变
    12.    * @param chars
    13.    * @param current
    14.    * @param perm
    15.    */
    16.   private static void dfs(char[] chars, int current, Deque<String> perm) {
    17.       int n = chars.length;
    18.       if (current == n) {
    19.           res.add(new ArrayList<>(perm));
    20.           return;
    21.       }
    22.       for (int i = current; i < n; i++) {
    23.           if (!checkPalindrome(chars, current, i)) {
    24.               continue;
    25.           }
    26.           //这个方法里面current就是从哪里开始截取，i + 1 - current是要截取的长度
    27.           perm.addLast(new String(chars, current, i + 1 - current));
    28.           //System.out.println("begin=="+perm);
    29.           dfs(chars,i+1,perm);
    30.           perm.removeLast();
    31.           //System.out.println("end=="+perm);
    32.       }
    33.   }
    34.    /**
    35.    * 判断是否为回文串，因为截取字符串是消耗性能的，所以就要传下标判断
    36.    * @param chars
    37.    * @param left
    38.    * @param right
    39.    * @return
    40.    */
    41.   private static boolean checkPalindrome(char[] chars, int left, int right) {
    42.       while (left < right) {
    43.           if (chars[left] != chars[right]) {
    44.               return false;
    45.           }
    46.           left++;
    47.           right--;
    48.       }
    49.       return true;
    50.   }

    解法2

  • 思路：回溯的优化，利用动态规划得到所有字串是否为回文。

  • 暂时还没有看懂，刷一遍动态规划后再回来写思路

    1.   static List<List<String>> res;
    2.   public static List<List<String>> partition3(String s) {
    3.       int len = s.length();
    4.       res = new ArrayList<>();
    5.       char[] chars = s.toCharArray();
    6.       boolean[][] dp = new boolean[len][len];
    7.       for (int right = 0; right < len; right++) {
    8.           for (int left = 0; left <= right; left++) {
    9.               if (chars[left] == chars[right] && (right - left <= 2 || dp[left + 1][right - 1])) {
    10.                   dp[left][right] = true;
    11.               }
    12.           }
    13.       }
    14.       Deque<String> perm = new ArrayDeque<>();
    15.       dfs2(s, 0, perm, len,dp);
    16.       return res;
    17.   }
    19.   private static void dfs2(String s, int current, Deque<String> perm, int len, boolean[][] dp) {
    20.       if (current == len) {
    21.           res.add(new ArrayList<>(perm));
    22.           return;
    23.       }
    24.       for (int i = current; i <len ; i++) {
    25.           if (dp[current][i]) {
    26.               perm.addLast(s.substring(current, i + 1));
    27.               dfs2(s, i + 1, perm, len, dp);
    28.               perm.removeLast();
    29.           }
    30.       }
    31.   }

    93.复原ip地址

    有效 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 ‘.’ 分隔。

    例如：”0.1.2.201” 和 “192.168.1.1” 是 有效 IP 地址，但是 “0.011.255.245”、”192.168.1.312” 和 “192.168@1.1” 是 无效 IP 地址。 给定一个只包含数字的字符串 s ，用以表示一个 IP 地址，返回所有可能的有效 IP 地址，这些地址可以通过在 s 中插入 ‘.’ 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。

    示例 1： 输入：s = “25525511135” 输出：[“255.255.11.135”,”255.255.111.35”]

    示例 2： 输入：s = “0000” 输出：[“0.0.0.0”]

    示例 3： 输入：s = “101023” 输出：[“1.0.10.23”,”1.0.102.3”,”10.1.0.23”,”10.10.2.3”,”101.0.2.3”]

    提示： 1 <= s.length <= 20 s 仅由数字组成

  • 思路：自己写的代码，思路难免会有点乱。截取字符串的方式与分割回文串解法1相同，都是用字符串的substring方法或者是用new String（）中的构造方法来截取。同时这题要用剪枝，如果这个字符串长度大于2，首位不能是0或者这个字符串不能超过4位且小于255。其实做了分割回文串这题就很好做了。

    1.   static List<String> res;
    2.   public static List<String> restoreIpAddresses(String s) {
    3.       res = new ArrayList<>();
    4.       List<String> perm = new ArrayList<>();
    5.       dfs(s, 0, perm);
    6.       return res;
    7.   }
    9.   private static void dfs(String s, int current, List<String> perm) {
    10.       int len = s.length();
    11.       if (current == len) {
    12.           if (perm.size() == 4) {
    13.               StringBuilder sb = new StringBuilder();
    14.               for (int i = 0; i < perm.size(); i++) {
    15.                   sb.append(perm.get(i));
    16.                   if (i != perm.size() - 1) {
    17.                       sb.append(".");
    18.                   }
    19.               }
    20.               res.add(sb.toString());
    21.               return;
    22.           }
    23.           return;
    24.       }
    25.       for (int i = current; i < len; i++) {
    26.           String substring = s.substring(current, i + 1);
    27.           if (substring.length() > 4) {
    28.               return;
    29.           }
    30.           if (i > current && (substring.charAt(0) == '0' || Integer.parseInt(substring) > 255)) {
    31.               continue;
    32.           }
    33.           if (perm.size() == 4) {
    34.               return;
    35.           }
    36.           perm.add(substring);
    37.           System.out.println("begin===" + perm);
    38.           dfs(s, i + 1, perm);
    39.           perm.remove(perm.size() - 1);
    40.           System.out.println("end==="+perm);
    41.       }
    42.   }