78.子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

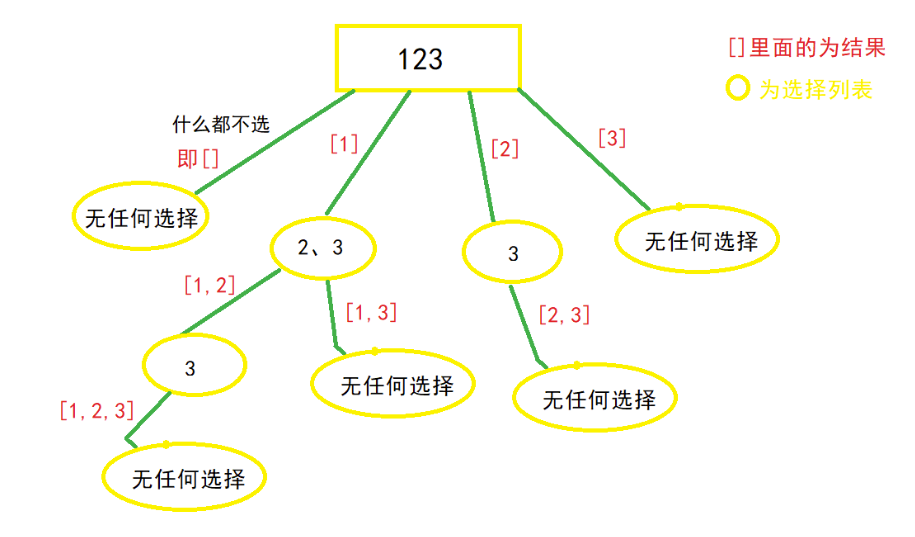
示例 1： 输入：nums = [1,2,3] 输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2： 输入：nums = [0] 输出：[[],[0]]

提示： 1 <= nums.length <= 10 -10 <= nums[i] <= 10 nums 中的所有元素 互不相同

解法1：回溯法

  • 思路：就是选和不选的问题，若选择了这个数字，则在perm集合里加上，若不选择，则直接递归到下一层。怎么解决选与不选：让循环i初始化时等于current，然后递归下去时用i+1来代替current+1，这时一种方法；而另一种方法则是不用for循环，而是直接选，然后递归下去，若干不选则是直接递归，这种方法就是下面代码内容。
  • 流程图

image.png

  1.     static List<List<Integer>> res;
  2.     public static List<List<Integer>> subsets(int[] nums) {
  3.         res = new ArrayList<>();
  4.         Deque<Integer> perm = new ArrayDeque<>();
  5.         dfs(nums, 0, perm);
  6.         return res;
  7.     }
  8.     private static void dfs(int[] nums, int current, Deque<Integer> perm) {
  9.         if (current == nums.length) {
  10.             res.add(new ArrayList<>(perm));
  11.             return;
  12.         }
  13.         //其实就是选和不选的问题
  14.         perm.addLast(nums[current]);
  15.         dfs(nums, current + 1, perm);
  16.         perm.removeLast();
  17.         //不选
  18.         dfs(nums, current + 1, perm);
  19.     }

解法2：二进制法

  • 思路：两层循环，第一层循环从0开始，循环的次数是子集的个数，第二层循环是子集的长度，从子集的长度减1开始到0结束。如果二进制位上为1，则把这个数字加进集合perm中，然后perm加进结果集合中。如1，2，3，有2^3=8个子集，则第一层要从0循环到7，0代表的二进制为000，1为001，2为010等等依次类推，第二层循环从子集长度-1为2开始0结束，0因为每一位都为0，所以加空集进perm中，1中的第二和第一位都为0，第一位为1，所以把3加进perm中，后面的结果依次类推。最后得到全部子集。
  1.  public static List<List<Integer>> subsets2(int[] nums) {
  2.         List<List<Integer>> ans = new ArrayList<>();
  3.         int len = nums.length;
  4.         Arrays.sort(nums);
  5.         for (int i = 0; i < (int) Math.pow(2, len); i++) {
  6.             List<Integer> perm = new ArrayList<>();
  7.             for (int j = len - 1; j >= 0; j--) {
  8.                 //i >> j & 1是把i右移j位，检测最低一位是否为1
  9.                 if ((i >> j & 1) == 1) {
  10.                     perm.add(nums[j]);
  11.                 }
  12.             }
  13.             ans.add(perm);
  14.         }
  15.         return ans;
  16.     }

90.子集II

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

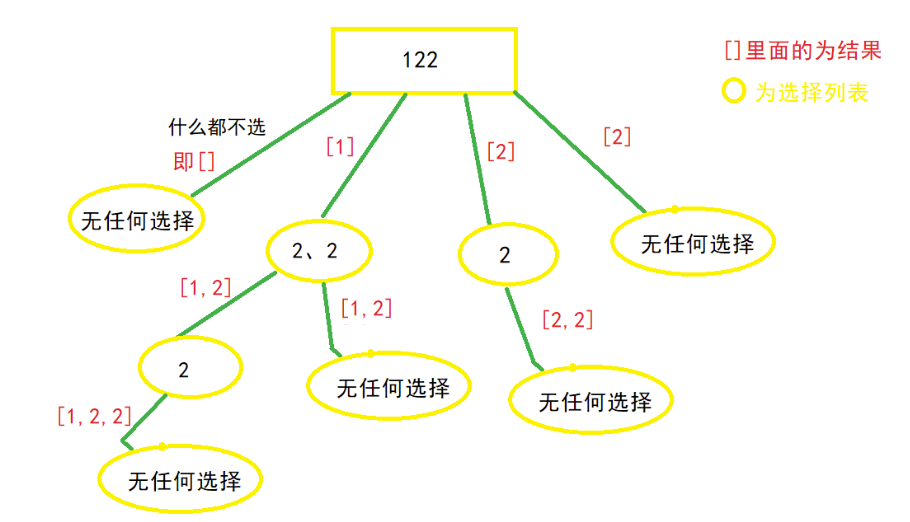
示例 1： 输入：nums = [1,2,2] 输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

示例 2： 输入：nums = [0] 输出：[[],[0]]

提示： 1 <= nums.length <= 10 -10 <= nums[i] <= 10

解法1：回溯法

  • 思路：这种解法同样有两种不同的代码写法，但是去重思路都是相同的。运用一个标志位，当这个元素的上一个标志位为false且num[i-1]==num[i]时，此时就不用把当前元素加进集合中。注意用循环时每次都要把当前的perm加入到结果中，而不用循环时要把不选放在选的后面。
  • 流程图

  • image.png

    1.   static List<List<Integer>> res;
    2.   public static List<List<Integer>> subsetsWithDup3(int[] nums) {
    3.       res = new ArrayList<>();
    4.       Deque<Integer> perm = new ArrayDeque<>();
    5.       boolean[] vis = new boolean[nums.length];
    6.       Arrays.sort(nums);
    7.       dfs2(nums, 0, perm, vis);
    8.       return res;
    9.   }
    10.   private static void dfs2(int[] nums, int current, Deque<Integer> perm, boolean[] vis) {
    11.       //先把当前路径加入到结果中
    12.       res.add(new ArrayList<>(perm));
    13.       int len = nums.length;
    14.       if (current == len) {
    15.           return;
    16.       }
    17.       for (int i = current; i < len; i++) {
    18.           if (i > 0 && nums[i - 1] == nums[i] && !vis[i - 1]) {
    19.               continue;
    20.           }
    21.           perm.addLast(nums[i]);
    22.           vis[i] = true;
    23.           dfs2(nums, i + 1, perm, vis);
    24.           vis[i] = false;
    25.           perm.removeLast();
    26.       }
    27.   }
    1.   static List<List<Integer>> res;
    2.   public static List<List<Integer>> subsetsWithDup2(int[] nums) {
    3.       res = new ArrayList<>();
    4.       Deque<Integer> perm = new ArrayDeque<>();
    5.       Arrays.sort(nums);
    6.       dfs(false,nums, 0, perm);
    7.       return res;
    8.   }
    10.   //画图帮助理解
    11.   private static void dfs(boolean choose,int[] nums, int current, Deque<Integer> perm) {
    12.       if (current == nums.length) {
    13.           res.add(new ArrayList<>(perm));
    14.           return;
    15.       }
    16.       //不选
    17.       dfs(false, nums, current + 1, perm);
    18.       //去重，上一层是不选的，且nums[current - 1] == nums[current]证明这个数是重复的
    19.       if (!choose && current > 0 && nums[current - 1] == nums[current]) {
    20.           return;
    21.       }
    22.       //选
    23.       perm.addLast(nums[current]);
    24.       dfs(true, nums, current + 1, perm);
    25.       perm.removeLast();
    26.   }

    解法2：二进制法

  • 思路：去重思路与解法1是相同的，若num[i-1]==num[i]时且没有选i-1这个数时，此时就要去重。

    1.   public static List<List<Integer>> subsetsWithDup(int[] nums) {
    2.       List<List<Integer>> ans = new ArrayList<>();
    3.       int len = nums.length;
    4.       Arrays.sort(nums);
    5.       for (int i = 0; i < (int) Math.pow(2, len); i++) {
    6.           List<Integer> perm = new ArrayList<>();
    7.           boolean flag = true;
    8.           for (int j = len - 1; j >= 0; j--) {
    9.               if ((i >> j & 1) == 1) {
    10.                   //找出规律可知，当nums[j - 1] == nums[j]且此时j-1位为0时，会输出重复的
    11.                   if (j > 0 && (i >> (j - 1) & 1) == 0 && nums[j - 1] == nums[j]) {
    12.                       flag = false;
    13.                       break;
    14.                   }
    15.                   perm.add(nums[j]);
    16.                   //System.out.println("perm=="+perm);
    17.               }
    18.           }
    19.           /*//用集合去重
    20.           if (!ans.contains(perm)) {
    21.               ans.add(perm);
    22.           }*/
    23.           if (flag) {
    24.               ans.add(perm);
    25.           }
    27.       }
    28.       return ans;
    29.   }