51.N皇后

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

示例 1： image.png 输入：n = 4 输出：[[“.Q..”,”…Q”,”Q…”,”..Q.”],[“..Q.”,”Q…”,”…Q”,”.Q..”]] 解释：如上图所示，4 皇后问题存在两个不同的解法。 示例 2： 输入：n = 1 输出：[[“Q”]]

提示： 1 <= n <= 9

  • 思路：循环i是对每一列进行循环，递归current是对每行进行循环。此时还要写一个check函数，同一列只能放一个棋子且要放的位置上的左右斜线都不能有棋子。当current==len时输出最终结果，且注意结果的输出形式要与题目给出的相同。

    1. static List<List<String>> res;
    2.   public static List<List<String>> solveNQueens(int n) {
    3.       res = new ArrayList<>();
    4.       char[][] board = new char[n][n];
    5.       for (int i = 0; i < n; i++) {
    6.           Arrays.fill(board[i], '.');
    7.       }
    8.       List<String> perm = new ArrayList<>();
    9.       dfs(n, board, perm, 0);
    10.       return res;
    11.   }
    13.   private static void dfs(int n,char[][] board, List<String> perm,int row) {
    14.       if (row == n) {
    15.           for (int i = 0; i < n; i++) {
    16.               StringBuilder sb = new StringBuilder();
    17.               for (int j = 0; j < n; j++) {
    18.                   sb.append(board[i][j]);
    19.               }
    20.               perm.add(sb.toString());
    21.           }
    22.           res.add(new ArrayList<>(perm));
    23.           perm.clear();
    24.       }
    25.       for (int j = 0; j < n; j++) {
    26.           if (check(n,board,row, j)) {
    27.               board[row][j] = 'Q';
    28.           }else continue;
    29.           dfs(n, board, perm, row + 1);
    30.           board[row][j] = '.';
    31.       }
    32.   }
    34.   private static boolean check(int n,char[][] board,int row, int list) {
    35.       if (row > 0) {
    36.           for (int i = row - 1; i >= 0; i--) {
    37.               if (board[i][list] == 'Q') {
    38.                   return false;
    39.               }
    40.           }
    41.           for (int i = 0; i < n; i++) {
    42.               for (int j = 0; j < n; j++) {
    43.                   if (j - i == list - row || j + i == list + row) {
    44.                       if (board[i][j] == 'Q') {
    45.                           return false;
    46.                       }
    47.                   }
    48.               }
    49.           }
    50.       }
    51.       return true;
    52.   }

    37.解数独

    编写一个程序，通过填充空格来解决数独问题。

    数独的解法需 遵循如下规则：

    数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图） 数独部分空格内已填入了数字，空白格用 ‘.’ 表示。

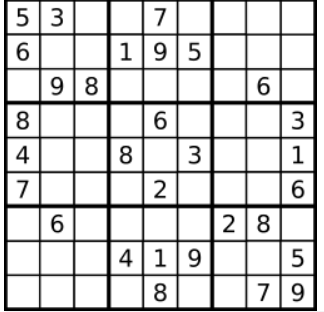
    示例 1： image.png

    输入：board = [[“5”,”3”,”.”,”.”,”7”,”.”,”.”,”.”,”.”],[“6”,”.”,”.”,”1”,”9”,”5”,”.”,”.”,”.”],[“.”,”9”,”8”,”.”,”.”,”.”,”.”,”6”,”.”],[“8”,”.”,”.”,”.”,”6”,”.”,”.”,”.”,”3”],[“4”,”.”,”.”,”8”,”.”,”3”,”.”,”.”,”1”],[“7”,”.”,”.”,”.”,”2”,”.”,”.”,”.”,”6”],[“.”,”6”,”.”,”.”,”.”,”.”,”2”,”8”,”.”],[“.”,”.”,”.”,”4”,”1”,”9”,”.”,”.”,”5”],[“.”,”.”,”.”,”.”,”8”,”.”,”.”,”7”,”9”]] 输出：[[“5”,”3”,”4”,”6”,”7”,”8”,”9”,”1”,”2”],[“6”,”7”,”2”,”1”,”9”,”5”,”3”,”4”,”8”],[“1”,”9”,”8”,”3”,”4”,”2”,”5”,”6”,”7”],[“8”,”5”,”9”,”7”,”6”,”1”,”4”,”2”,”3”],[“4”,”2”,”6”,”8”,”5”,”3”,”7”,”9”,”1”],[“7”,”1”,”3”,”9”,”2”,”4”,”8”,”5”,”6”],[“9”,”6”,”1”,”5”,”3”,”7”,”2”,”8”,”4”],[“2”,”8”,”7”,”4”,”1”,”9”,”6”,”3”,”5”],[“3”,”4”,”5”,”2”,”8”,”6”,”1”,”7”,”9”]] 解释：输入的数独如上图所示，唯一有效的解决方案如下所示： image.png 提示： board.length == 9 board[i].length == 9 board[i][j] 是一位数字或者 ‘.’ 题目数据 保证 输入数独仅有一个解

  • 思路：首先注意到题目给出的函数为void值，在力扣中在void的函数中能给出boolean值就能得到输出结果，不用自己写输出语句。思路其实和N皇后差不多，只是check函数有较大的差别。

    1. public static void solveSudoku2(char[][] board) {
    2.       //力扣中dfs2中输出结果是boolean型就能输出题目所要结果
    3.       dfs2(board, 0, 0);
    4.   }
    5.   private static boolean dfs2(char[][] board, int row, int list) {
    6.       if (row > 8) {
    7.           return true;
    8.       }
    9.       if (board[row][list] == '.') {
    10.           for (char i = '1'; i <= '9'; i++) {
    11.               if (check(board, row, list, i)) {
    12.                   board[row][list] = i;
    13.                   if (!dfs2(board, row + ((list + 1) / 9), (list + 1) % 9)) board[row][list] = '.';
    14.                   else return true;
    15.               }
    16.           }
    17.       }else {
    18.           return dfs2(board, row + ((list + 1) / 9), (list + 1) % 9);
    19.       }
    20.       return false;
    21.   }
    23.   private static boolean check(char[][] board, int row, int list,char num) {
    24.       for (int i = 0; i < 9; i++) {
    25.           if (board[row][i] == num) return false;
    26.           if (board[i][list] == num) return false;
    27.       }
    28.       //这段判断小九宫格有错误
    29.       /*for (int i = - 1; i < 2 ; i++) {
    30.           for (int j = -1; j < 2; j++) {
    31.               if (row + i >= 0 && list + j >= 0 && row + i < 9 && list + j < 9) {
    32.                   if (board[row + i][list + j] == num) return false;
    33.               }
    34.           }
    35.       }*/
    36.       for (int i = (row / 3) * 3; i < (row / 3 + 1) * 3; i++) {
    37.           for (int j = (list / 3) * 3; j < (list / 3 + 1) * 3; j++) {
    38.               if (board[i][j] == num) return false;
    39.           }
    40.       }
    41.       return true;
    42.   }