77.组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1： 输入：n = 4, k = 2 输出： [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]

示例 2： 输入：n = 1, k = 1 输出：[[1]]

提示： 1 <= n <= 20 1 <= k <= n

  • 思路：这是一道经典的不考虑顺序的问题，即选和不选问题，解决这道题有两种不同的代码，第一种是直接用递归进行选和不选操作，第二种用循环中包含递归，递归i从current开始，循环下去就是选和不选的问题。这道题关键是剪枝，当集合perm的长度加上区间[i,n]的长度比k小时，这时候就不用递归下去了。
  • 流程图

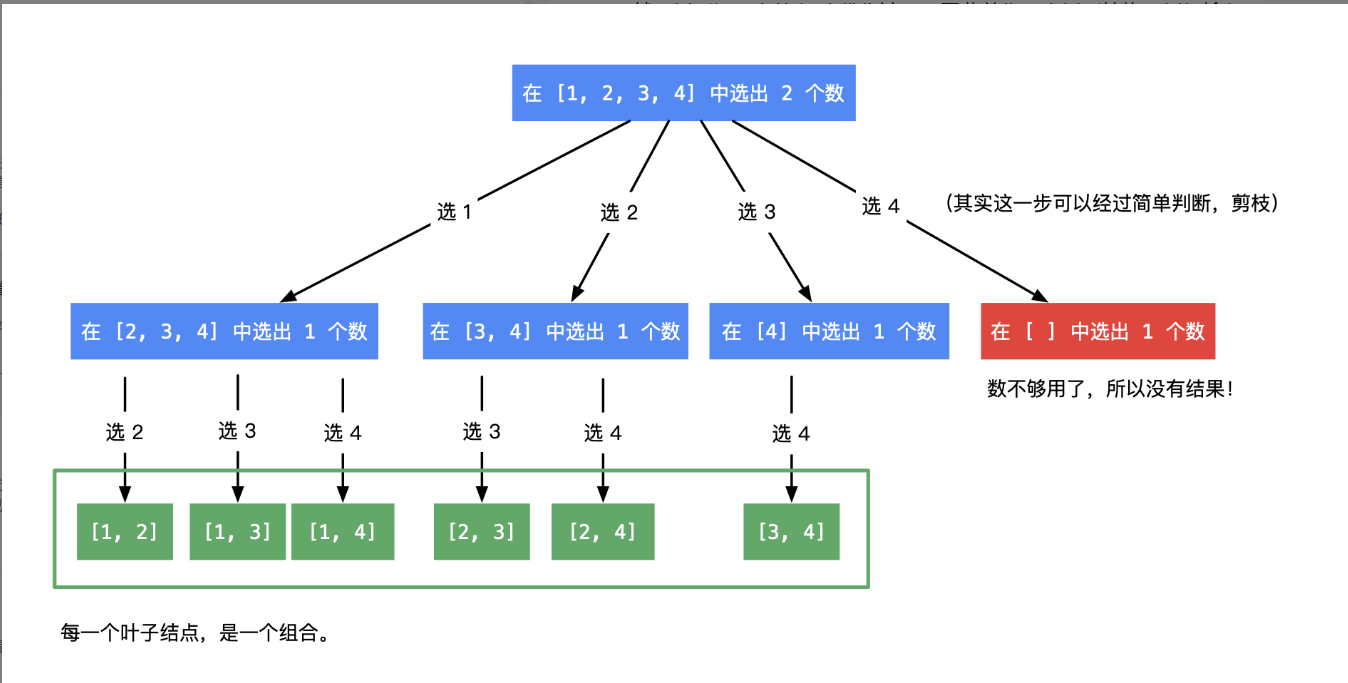
image.png

  1.     static List<List<Integer>> res;
  2.     public static List<List<Integer>> combine2(int n, int k) {
  3.         res = new ArrayList<>();
  4.         List<Integer> perm = new ArrayList<>();
  5.         dfs(1, n, k,perm);
  6.         return res;
  7.     }
  9.     private static void dfs(int current, int n, int k, List<Integer> perm) {
  10.         //剪枝：perm长度加上区间 [current, n] 的长度小于 k，不可能构造出长度为 k 的 perm
  11.         if (perm.size() + (n - current + 1) < k) {
  12.             return;
  13.         }
  14.         if (perm.size() == k) {
  15.             res.add(new ArrayList<>(perm));
  16.             return;
  17.         }
  19.         //选择当前current这个数
  20.         perm.add(current);
  21.         dfs(current + 1, n, k, perm);
  22.         perm.remove(perm.size() - 1);
  23.         //不选择current这个数
  24.         dfs(current + 1, n, k, perm);
  25.     }
  1.     static List<List<Integer>> res;
  2.     public static List<List<Integer>> combine3(int n, int k) {
  3.         res = new ArrayList<>();
  4.         List<Integer> perm = new ArrayList<>();
  5.         dfs2(1, n, k,perm);
  6.         return res;
  7.     }
  9.     private static void dfs2(int current, int n, int k, List<Integer> perm) {
  10.         if (perm.size() == k) {
  11.             res.add(new ArrayList<>(perm));
  12.             return;
  13.         }
  14.         for (int i = current; i <= n; i++) {
  15.             //剪枝，当perm的长度加上区间[i，n]的长度不足k时，剪枝
  16.             if (perm.size() + (n - i + 1) < k) {
  17.                 return;
  18.             }
  19.             perm.add(i);
  20.             System.out.println("begin=="+perm);
  21.             dfs2(i + 1, n, k, perm);
  22.             perm.remove(perm.size() - 1);
  23.             System.out.println("end=="+perm);
  24.         }
  25.     }

216.组合总和III

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

只使用数字1到9 每个数字 最多使用一次 返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例 1: 输入: k = 3, n = 7 输出: [[1,2,4]] 解释: 1 + 2 + 4 = 7 没有其他符合的组合了。

示例 2: 输入: k = 3, n = 9 输出: [[1,2,6], [1,3,5], [2,3,4]] 解释: 1 + 2 + 6 = 9 1 + 3 + 5 = 9 2 + 3 + 4 = 9 没有其他符合的组合了。

示例 3: 输入: k = 4, n = 1 输出: [] 解释: 不存在有效的组合。 在[1,9]范围内使用4个不同的数字，我们可以得到的最小和是1+2+3+4 = 10，因为10 > 1，没有有效的组合。

提示: 2 <= k <= 9 1 <= n <= 60

  • 思路：和组合的思路差不多，只是最后得出结果和剪枝不同，最后的结果要相加等于n才能加进res中，剪枝条件时当相加结果大于n时，剪枝。

    1. static List<List<Integer>> res;
    2.   public static List<List<Integer>> combinationSum3(int n, int k) {
    3.       res = new ArrayList<>();
    4.       List<Integer> perm = new ArrayList<>();
    5.       combinationSum3Core(n, k, 1, perm,0);
    6.       return res;
    7.   }
    9.   private static void combinationSum3Core(int n, int k, int current, List<Integer> perm, int sum) {
    10.       if (sum > n) {
    11.           return;
    12.       }
    13.       if (perm.size() == k) {
    14.           if (n == sum) {
    15.               res.add(new ArrayList<>(perm));
    16.           }
    17.           return;
    18.       }
    19.       for (int i = current; i < 10; i++) {
    20.           perm.add(i);
    21.           sum += i;
    22.           combinationSum3Core(n, k, i + 1, perm, sum);
    23.           sum -= i;
    24.           perm.remove(perm.size() - 1);
    25.       }
    26.   }

    17.电话号码的字母组合

    给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。 image.png 示例 1： 输入：digits = “23” 输出：[“ad”,”ae”,”af”,”bd”,”be”,”bf”,”cd”,”ce”,”cf”]

    示例 2： 输入：digits = “” 输出：[]

    示例 3： 输入：digits = “2” 输出：[“a”,”b”,”c”]

    提示： 0 <= digits.length <= 4 digits[i] 是范围 [‘2’, ‘9’] 的一个数字。

  • 思路：先把数字对应的字母表示下来，可以用map或者if，switch都可以，再将对应的字母按题目要求输出。

  • 流程图：

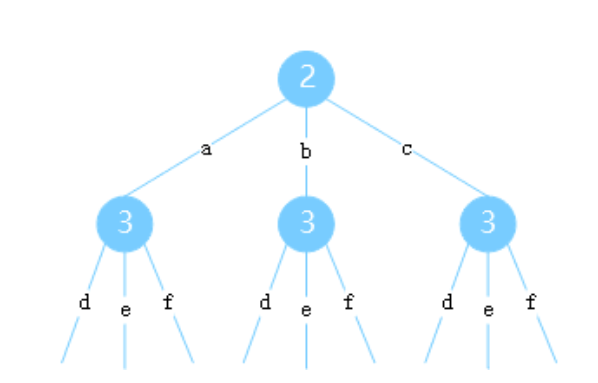
image.png

  1. static List<String> res;
  2.     public static List<String> letterCombinations(String digits) {
  3.         res = new ArrayList<>();
  4.         if (digits.equals("")) {
  5.             return res;
  6.         }
  7.         char[] chars = digits.toCharArray();
  8.         char[] temp = new char[chars.length];
  9.         List<String> words = new ArrayList<>();
  10.         for (char aChar : chars) {
  11.             words.add(digitsToWords(aChar));
  12.         }
  13.         letterCombinationsCore(digits,words, 0,  temp);
  14.         return res;
  15.     }
  17.     private static void letterCombinationsCore(String digits,List<String> words, int current, char[] temp) {
  18.         if (current == digits.length()) {
  19.             //Arrays.toString是打印数组内容，String.valueOf才是从char类型转化为String类型
  20.             res.add(String.valueOf(temp));
  21.             return;
  22.         }
  23.         String s = words.get(current);
  24.         for (int i = 0; i < s.length(); i++) {
  25.             temp[current] = s.charAt(i);
  26.             letterCombinationsCore(digits,words, current + 1, temp);
  27.         }
  28.     }
  30.     static String digitsToWords(char c) {
  31.         switch (c) {
  32.             case '2':
  33.                 return "abc";
  34.             case '3':
  35.                 return "def";
  36.             case '4':
  37.                 return "ghi";
  38.             case '5':
  39.                 return "jkl";
  40.             case '6':
  41.                 return "mno";
  42.             case '7':
  43.                 return "pqrs";
  44.             case '8':
  45.                 return "tuv";
  46.             case '9':
  47.                 return "wxyz";
  48.             default:
  49.                 return " ";
  50.         }
  51.     }

39.组合总和

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1： 输入：candidates = [2,3,6,7], target = 7 输出：[[2,2,3],[7]] 解释： 2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。 7 也是一个候选， 7 = 7 。 仅有这两种组合。

示例 2： 输入: candidates = [2,3,5], target = 8 输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3： 输入: candidates = [2], target = 1 输出: []

提示： 1 <= candidates.length <= 30 1 <= candidates[i] <= 200 candidate 中的每个元素都 互不相同 1 <= target <= 500

  • 思路：和216题不同的地方，就是每个元素都可以重复使用，此时数据很多，必须要进行剪枝。现在不用sum了，而是每次递归都对目标数进行相减，如果下一个数大于目标数，则直接剪枝。要实现剪枝，最后就先对数组进行排序。
  • 流程图

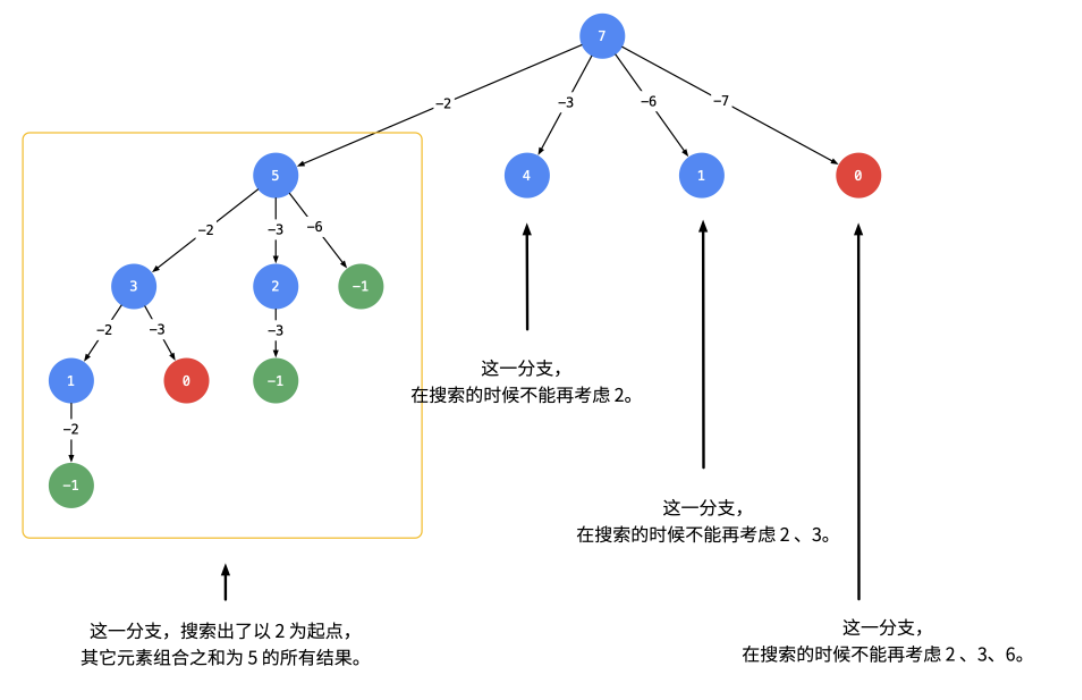
image.png

  1.     static List<List<Integer>> res;
  2.     public static List<List<Integer>> combinationSum2(int[] candidates, int target) {
  3.         res = new ArrayList<>();
  4.         //用这个删除尾部元素比用ArrayList性能好一点
  5.         Deque<Integer> perm = new ArrayDeque<>();
  6.         Arrays.sort(candidates);
  7.         combinationSum2Core(candidates, target, 0, perm);
  8.         return res;
  9.     }
  11.     private static void combinationSum2Core(int[] candidates, int target, int current, Deque<Integer> perm) {
  12.         if (target == 0) {
  13.             res.add(new ArrayList<>(perm));
  14.             return;
  15.         }
  16.         for (int i = current; i < candidates.length; i++) {
  17.             //剪枝
  18.             if (target - candidates[i] < 0) {
  19.                 break;
  20.             }
  21.             perm.add(candidates[i]);
  22.             target -= candidates[i];
  23.             System.out.println("递归之前:" + perm + "剩余:" + target);
  24.             //因为可以重复，所以从i开始
  25.             combinationSum2Core(candidates, target, i, perm);
  26.             target += candidates[i];
  27.             perm.removeLast();
  28.             System.out.println("递归之后:" + perm + "剩余:" + target);
  29.         }
  30.     }

40.组合总和II

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

注意：解集不能包含重复的组合。

示例 1: 输入: candidates = [10,1,2,7,6,1,5], target = 8, 输出: [[1,1,6], [1,2,5], [1,7], [2,6]]

示例 2: 输入: candidates = [2,5,2,1,2], target = 5, 输出: [[1,2,2],[5]]

  • 思路：这题和39题思路也差不多，只是多了个去重的步骤，因为题目中说解集不能包含重复的子集，要去重，思路都是大同小异的，先进行排序，让相同的数字相邻，并且同一层每个相同的数都使用首次出现的。
  • 流程图

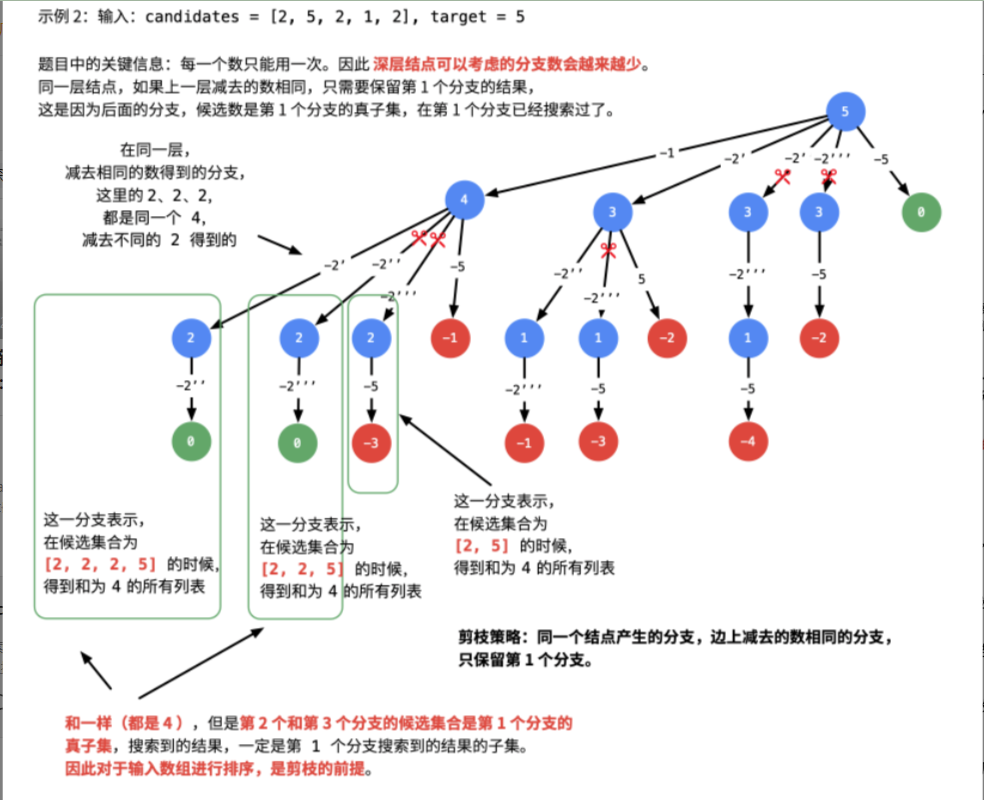
image.png

  1.     static List<List<Integer>> res;
  2.     static int n;
  3.     public static List<List<Integer>> combinationSum2(int[] candidates, int target) {
  4.         res = new ArrayList<>();
  5.         Deque<Integer> perm = new ArrayDeque<>();
  6.         Arrays.sort(candidates);
  7.         n = 0;
  8.         combinationSum2Core(candidates, target, 0, perm);
  9.         return res;
  10.     }
  12.     private static void combinationSum2Core(int[] candidates, int target, int current, Deque<Integer> perm) {
  13.         if (target == 0) {
  14.             res.add(new ArrayList<>(perm));
  15.             return;
  16.         }
  17.         for (int i = current; i < candidates.length; i++) {
  18.             //剪枝，让perm首位已经出现过的不会再出现
  19.             if (i > current && candidates[i - 1] == candidates[i]) {
  20.                 continue;
  21.             }
  22.             if (target - candidates[i] < 0) {
  23.                 break;
  24.             }
  25.             perm.add(candidates[i]);
  26.             target -= candidates[i];
  27.             System.out.println("begin:" + perm + "remain" + target);
  28.             combinationSum2Core(candidates, target, i + 1, perm);
  29.             target += candidates[i];
  30.             perm.removeLast();
  31.             System.out.println("end" + perm + "remain" + target);
  32.         }
  33.     }