46.全排列I

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1： 输入：nums = [1,2,3] 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2： 输入：nums = [0,1] 输出：[[0,1],[1,0]]

示例 3： 输入：nums = [1] 输出：[[1]]

提示： 1 <= nums.length <= 6 -10 <= nums[i] <= 10 nums 中的所有整数 互不相同

解法1

  • 思路：利用swag函数，每次递归都进行一次调换，在递归结束后再次调用swag函数让排列复原。

  • 比如字符串abc，k=0时，先拿a，k=1时，可以拿b和c，k=2时，ab可以拿c，ac可以拿b，同样的k=0时也可以拿b或c，后面的思路相同，这里讲一种，比如k=0时拿a，递归下去k加1此时k=1时拿b，继续递归k=2拿c，继续递归k=3时把abc加进目标集合res中，此时获得一次结果，这条支路的结果走到底了，这时开始回溯，i=k=3大于chars数组长度，跳出for循环，继续回溯，i=k=2，i++后也大于数组长度，继续回溯， i=k=1，i++后i=2，可以进入循环，此时char[1]与char[2]交换，得到acb，然后进入递归，直到k=3时把acb加进res中，又获得一次结果 这条支路也走完了，继续回溯，直到又回溯到k=1的情况时，i=2，此时char[1]与char[2]交换，重新得到abc，之后i++为3跳出循环，回溯，k=i=0 i++后i=1，这时char[0]与char[1]交换，得到bac，后面思路同上类似

    1.   static List<List<Integer>> res = new ArrayList<>();
    2.   public static List<List<Integer>> permute1(int[] nums) {
    3.       res.clear();
    4.       Arrays.sort(nums);
    5.       permuteCore(nums,0);
    6.       return res;
    7.   }
    8.   private static void permuteCore(int[] nums, int current) {
    9.       if (current == nums.length) {
    10.           List<Integer> list = new ArrayList<>();
    11.           for (int num : nums) {
    12.               list.add(num);
    13.           }
    14.           res.add(list);
    15.           return;
    16.       }
    17.       for (int i = current; i < nums.length ; i++) {
    18.           swag(nums,i,current);
    19.           permuteCore(nums, current + 1);
    20.           swag(nums, i, current);
    21.       }
    22.   }
    23.   static void swag(int[] num, int i, int j) {
    24.       int temp = 0;
    25.       temp = num[i];
    26.       num[i] = num[j];
    27.       num[j] = temp;
    28.   }

    解法2

  • 思路：使用users数组，该数组的下标对应题目给出的nums数组的下标，nums数组对应的下标用过后，users[i] = ture，否则为false。并且这个循环i是从0开始而不是current开始的，原因就是从0开始可以让nums数组中所有数字都可以放在第一位并且让nums数组中每个元素都能在集合中；而从current开始是解决选和不选的问题

  • 流程图

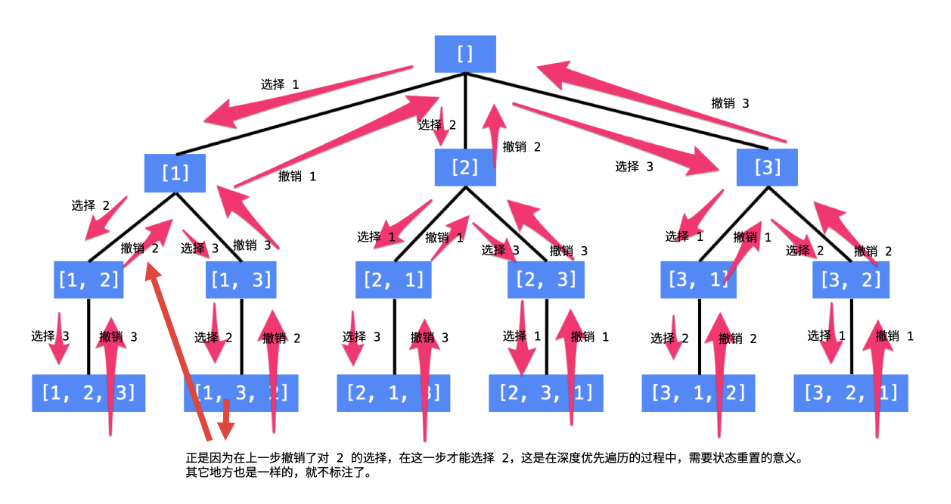
image.png

  1.     //解法2使用users数组
  2.     static List<List<Integer>> res = new ArrayList<>();
  3.     public static List<List<Integer>> permute2(int[] nums) {
  4.         res = new ArrayList<>();
  5.         Deque<Integer> perm = new ArrayDeque<>();
  6.         boolean[] used = new boolean[nums.length];
  7.         permute2Core(nums, 0, perm, used);
  8.         return res;
  9.     }
  11.       private static void permute2Core(int[] nums, int current, Deque<Integer> perm, boolean[] used) {
  12.         int len = nums.length;
  13.         if (current == len) {
  14.             res.add(new ArrayList<>(perm));
  15.             return;
  16.         }
  17.         for (int i = 0; i < len; i++) {
  18.             if (!used[i]) {
  19.                 perm.addLast(nums[i]);
  20.                 used[i] = true;
  21.                 permute2Core(nums, current + 1, perm, used);
  22.                 used[i] = false;
  23.                 perm.removeLast();
  24.             }
  25.         }
  26.     }

47.全排列II

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1： 输入：nums = [1,1,2] 输出：[[1,1,2], [1,2,1],[2,1,1]]

示例 2： 输入：nums = [1,2,3] 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示： 1 <= nums.length <= 8 -10 <= nums[i] <= 10

解法1

  • 利用Set集合去重，但这种方法时间复杂度太大，所以不在这里展示

    解法2

  • 与全排列I解法2中思路类似，都是用used（vis）数组来标记已经填过的数字，如果没有填过，就加进集合perm中并将这个数字标记

  • 对于解决重复问题，要先排序，保证相同的数相邻，然后在填current个数时重复数只会填入一次即可，并且写 !vis[i - 1] 是因为 nums[i - 1] 在深度优先遍历的过程中刚刚被撤销选择，比如1,1’,2，1,1’,2不能被剪枝，而1’,1,2这种情况就要被剪叶
  • 流程图

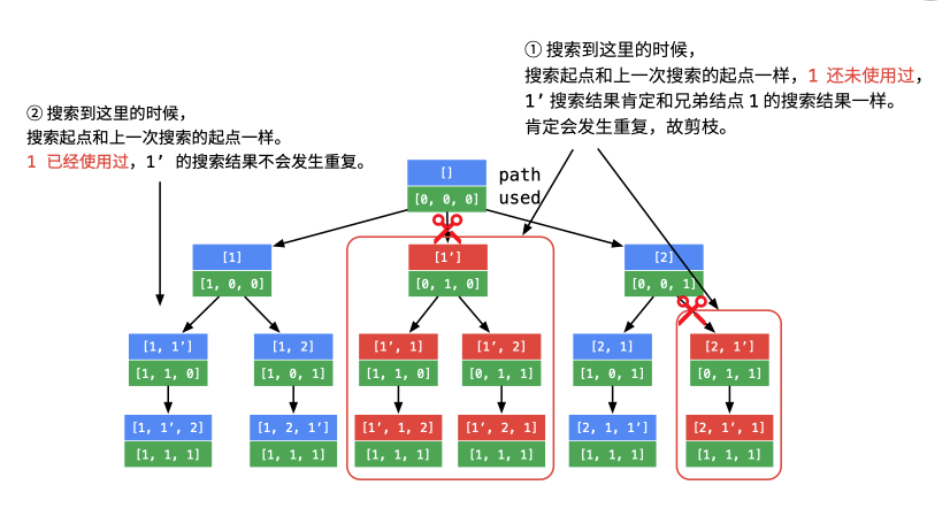
image.png

  1.     static List<List<Integer>> res;
  2.     static boolean[] vis;
  3.     public static List<List<Integer>> permuteUnique2(int[] nums) {
  4.         //先排序，让数组中相同的数靠近
  5.         Arrays.sort(nums);
  6.         res = new ArrayList<>();
  7.         List<Integer> perm = new ArrayList<>();
  8.         vis = new boolean[nums.length];
  9.         permuteUniqueCore2(nums, 0, perm);
  10.         return res;
  11.     }
  12.     private static void permuteUniqueCore2(int[] nums, int current, List<Integer> perm) {
  13.         int n = nums.length;
  14.         if (current == n) {
  15.             res.add(new ArrayList<>(perm));
  16.             return;
  17.         }
  18.         for (int i = 0; i < n; i++) {
  19.             // 剪枝条件：i > 0 是为了保证 nums[i - 1] 有意义
  20.             // 写 !vis[i - 1] 是因为 nums[i - 1] 在深度优先遍历的过程中刚刚被撤销选择
  21.             if (vis[i] || (i > 0 && nums[i] == nums[i - 1] && !vis[i - 1])) {
  22.                 continue;
  23.             }
  24.             perm.add(nums[i]);
  25.             vis[i] = true;
  26.             permuteUniqueCore2(nums, current + 1, perm);
  27.             vis[i] = false;
  28.             perm.remove(current);
  29.         }
  30.     }

总结

  • 排序问题因为结果要求拥有每一个元素，所以循环i要从0开始，并且已经填入过的元素不能够再次填入，所以使用used（vis）数组来确保已经填入的元素不会再填入
  • 排序中重复的元素要根据树状图，画出思路来剪枝