归并排序

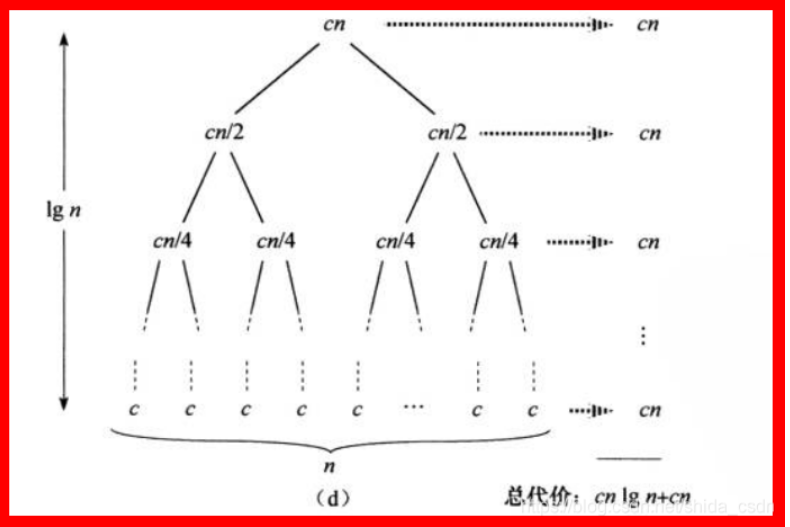
时间复杂度：O(nlogn)空间复杂度：O(n+logn).归并的空间复杂度就是那个临时的数组和递归时压入栈的数据占用的空间：n + logn；所以空间复杂度为: O(n)最好情况和最坏情况都是O(nlogn)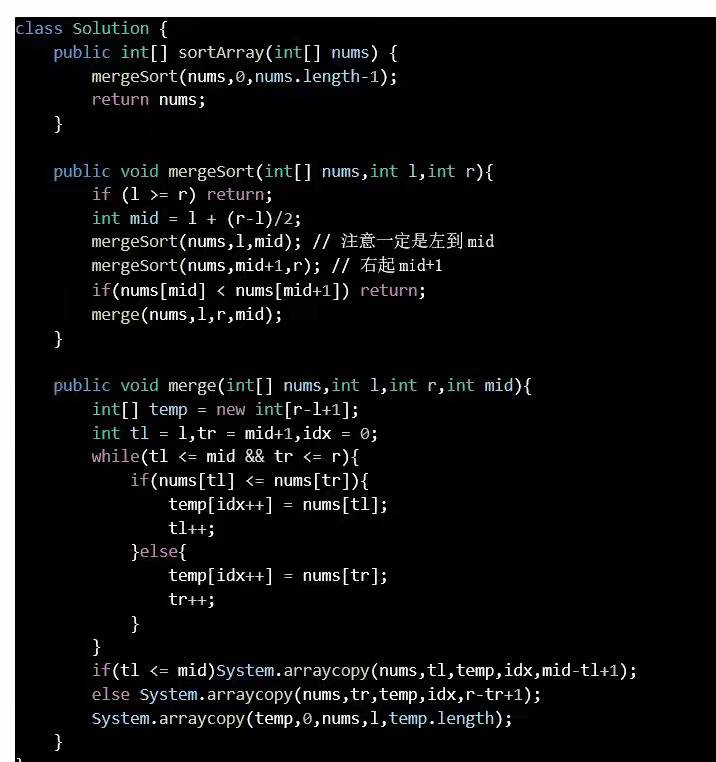

归并时间复杂度分析

2、System.arraycopy的函数原型是：
public static void arraycopy(Object src,
int srcPos,
Object dest,
int destPos,
int length)
其中：src表示源数组，srcPos表示源数组要复制的起始位置，desc表示目标数组，length表示要复制的长度。

• System.arraycopy，JVM 提供的数组拷贝实现。本地方法

快速排序

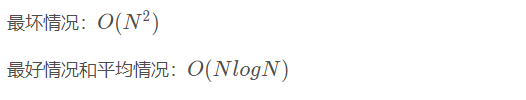
最优的情况下空间复杂度为：O(logn) ；每一次都平分数组的情况
最差的情况下空间复杂度为：O( n ) ；退化为冒泡排序的情况

二. 快速排序优化：随机选取基准值base

在数组几乎有序时，快排性能不好(因为每趟排序后，左右两个子递归规模相差悬殊，大的那部分最后很可能会达到O(n^2))。

解决：基准值随机地选取，而不是每次都取第一个数。这样就不会受“几乎有序的数组”的干扰了。但是对“几乎乱序的数组”的排序性能可能会稍微下降，至少多了排序前交换的那部分，乱序时这个交换没有意义…有很多“运气”成分..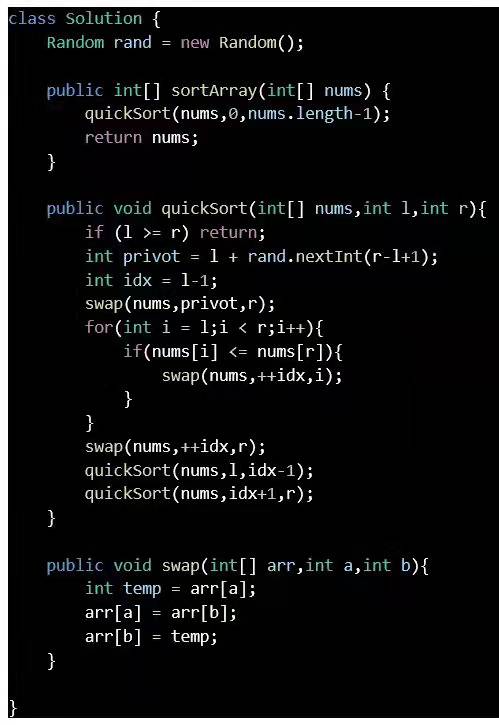

/就不至于在数组相对有序时，导致左右两边的递归规模不一致，产生最坏时间复杂度
由于一般哨兵节点都选取最左边或最右边的元素，容易造成时间复杂度为O(N*N)的情况（原数组有序

快速排序的基本思想是

1、先从数列中取出一个数作为基准数<br />    2、分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边<br />    3、再对左右[区间](https://so.csdn.net/so/search?q=%E5%8C%BA%E9%97%B4&spm=1001.2101.3001.7020" \t "https://blog.csdn.net/asdfsadfasdfsa/article/details/_blank)重复第二步，直到各区间只有一个数

时间复杂度：最好情况：O(nlog2n)最坏情况：O(n2)
空间复杂度：O(log2n)
稳定性：不稳定

1、当某个区间需要排序的数据为一定范围时，进行直接插入排序

###双指针法

定义变量cur指向序列的开头，定义变量pre指向cur的前一个位置。
当array[cur] < key时，cur和pre同时往后走，如果array[cur]>key，cur往后走，pre留在大于key的数值前一个位置。
当array[cur]再次 < key时，交换array[cur]和array[pre]。
通俗一点就是，在没找到大于key值前，pre永远紧跟cur，遇到大的两者之间机会拉开差距，中间差的肯定是连续的大于key的值，当再次遇到小于key的值时，交换两个下标对应的值就好了。
带着这种思想，看着图示应该就能理解了。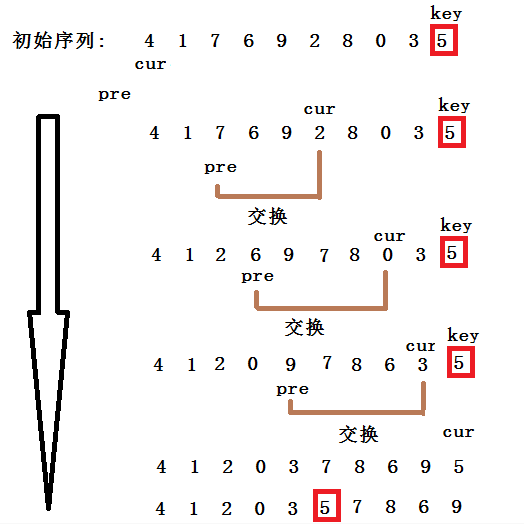

堆排序

算法复杂度：O(nlogn)
1.建堆的时间复杂度为O(n);O(log1) + O(log2) + O(log3) + … O(logn) = O(n)
2、取值后重新调整堆
取值每次取的都是堆顶元素，取完重新调整的次数都是k次，时间复杂度就是也就是logn，而循环要执行n次，所以取值后重新调整堆得时间复杂度就是O(nlogn);
空间复杂度为常数：O(1) 直接对现有的数据结构进行排序，因此是O ( 1 )

1、首先了解堆是什么

堆是一种数据结构，一种叫做完全二叉树的数据结构。

1 堆的性质

1. 一般升序采用大顶堆，降序采用小顶堆)。

这里我们用到两种堆，其实也算是一种。
大顶堆：每个节点的值都大于或者等于它的左右子节点的值。
小顶堆：每个节点的值都小于或者等于它的左右子节点的值。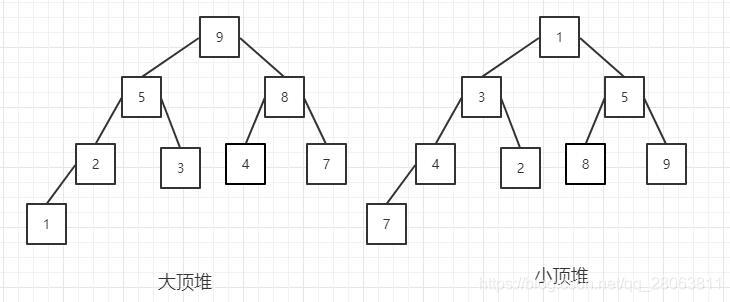

：1、将带排序的序列构造成一个大顶堆，根据大顶堆的性质，当前堆的根节点（堆顶）就是序列中最大的元素；2、将堆顶元素和最后一个元素交换，然后将剩下的节点重新构造成一个大顶堆；3、重复步骤2，如此反复，从第一次构建大顶堆开始，每一次构建，我们都能获得一个序列的最大值，然后把它放到大顶堆的尾部。最后，就得到一个有序的序列了。（升序）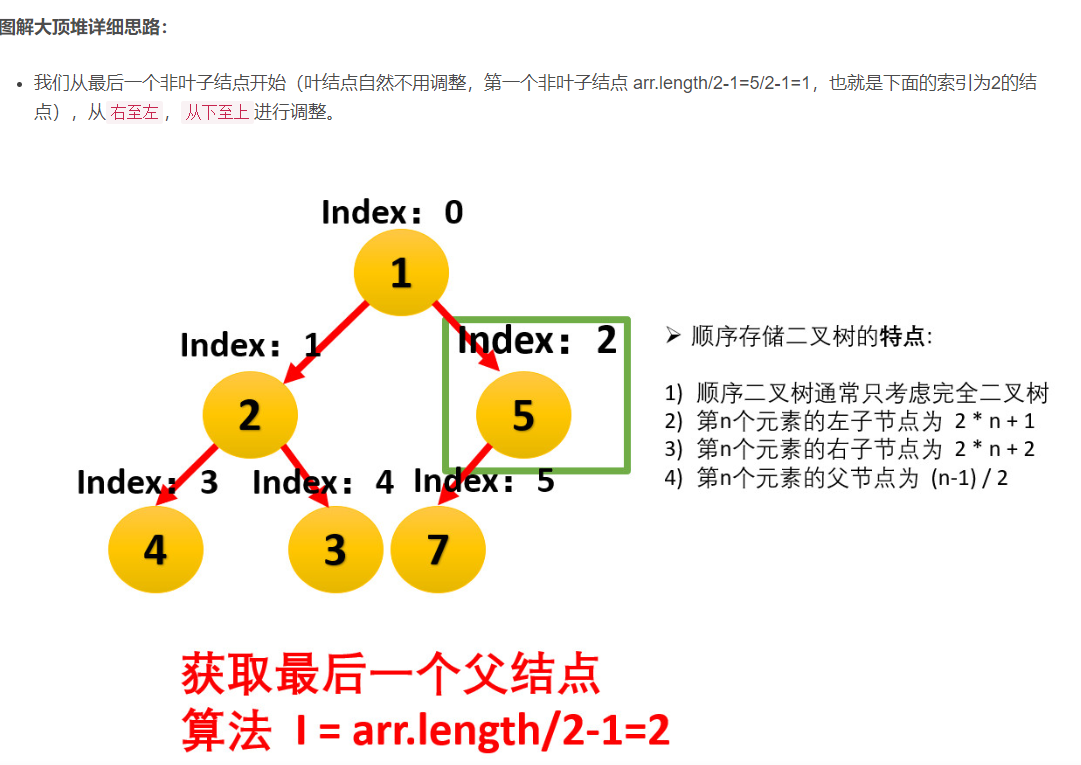

为什么要使用temp优化？

目的：省去交换次数，用temp记录最大值，这样循环就不用每次交换了
两个重要的参数
for (int i = arr.length / 2 - 1; i >= 0; i—) {
//从第一个非叶子结点从下至上，从右至左调整结构

k = i 2 + 1; k < length; k = k 2 + 1) {//从i结点的左子结点开始

冒泡排序

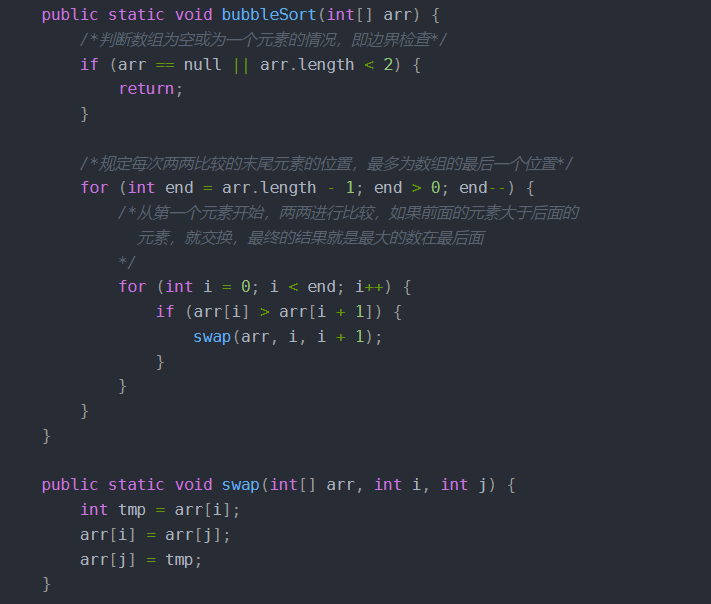
其思想是相邻的元素两两比较，较大的数下沉，较小的数冒起来，这样一趟比较下来，最大(小)值就会排列在一端。整个过程如同气泡冒起，因此被称作冒泡排序。
冒泡排序的步骤是比较固定的：
1>比较相邻的元素。如果第一个比第二个大，就交换他们两个。
2>每趟从第一对相邻元素开始，对每一对相邻元素作同样的工作，直到最后一对。
3>针对所有的元素重复以上的步骤，除了已排序过的元素(每趟排序后的最后一个元素)，直到没有任何一对数字需要比较。
具体实现

时间复杂度

为何要有树这种结构？