这些latex的语法基本已经涵盖了我平时阅读文章做笔记时需要使用的latex工具

基础语法

帽子

\hat{x}

分数

\frac{1}{2}

上标

^{2}

下标

_{system},单个字母可无需花括号

花括号

\left\{ \frac{a}{b} \right\}

求和

\sum\limits_{j=1}^{M}

矩阵

\begin{gathered}
\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}
\quad
\begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix}
\quad
\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}
\quad
\begin{Bmatrix} 1 & 0 \\ 0 & -1 \end{Bmatrix}
\quad
\begin{vmatrix} a & b \\ c & d \end{vmatrix}
\quad
\begin{Vmatrix} i & 0 \\ 0 & -i \end{Vmatrix}
\end{gathered}

空格

\quad

优化理论相关

二范数的平方

\Vert f-z\Vert^{2}

\|f-z\|_2^2

梯度操作

\nabla

偏微分

\frac{\partial f}{\partial x} # 一阶
\frac{\partial ^{n} f}{\partial x^{n}} # n阶

argmin

\mathop{argmin}\limits_{\theta}

傅里叶变换

\mathscr{F}^{-1}

花体

\mathcal

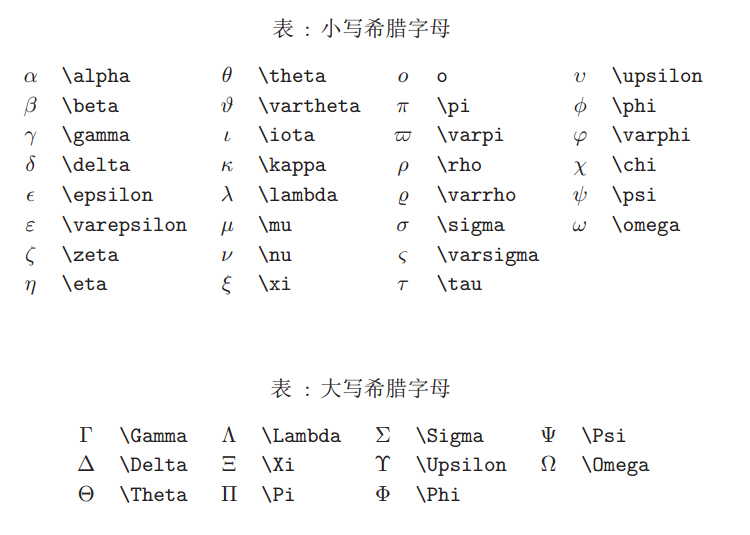
希腊字母

特殊符号

\mathbb{R}
\in

实战使用

\|\mathbf{u}_{x x}-\mathbf{g}_{x x}-\mathbf{v}_{x x}\|

\nabla_{x x}^{T}\cdot[g_{xx}-(u_{xx}-v_{xx})]

\nabla_{y y}, \nabla_{t t}, \nabla_{x y}, \nabla_{x t}, \nabla_{y t}

\frac{\lambda \mu_{1}}{2}\|x-\mathcal{S H}(u)-\tilde{x}\|_{2}^{2}

TV(x) = ||\nabla_xx||_1+||\nabla_yx||_1 =\begin{Vmatrix}\begin{bmatrix} \nabla_x \\ \nabla_y \end{bmatrix}x\end{Vmatrix}_1

换行

\\

公式左对齐

\begin{align} & X(0) = x(0)W_{N}^{0\cdot0} + x(1)W_{N}^{0\cdot1} + \cdots + x(N-1)W_{N}^{0\cdot(N-1)}\\ & X(1) = x(0)W_{N}^{1\cdot0} + x(1)W_{N}^{1\cdot1} + \cdots + x(N-1)W_{N}^{1\cdot(N-1)} \\ & \cdots \\ & X(N-1) = x(0)W_{N}^{(N-1)\cdot0} + x(1)W_{N}^{(N-1)\cdot1} + \cdots + x(N-1)W_{N}^{(N-1)\cdot(N-1)} \\ \end{align}

箭头

\rightarrow