设计算法寻找最优路径

穷举法

计算所有可能路径
缺点：计算量太大。

A*算法

每一步只走最好走的路。
优点：计算快，而且这种贪心或者说启发式的算法，通常情况下，效果还是不错的
缺点：不一定能算出最优解

beam search

每一步只走最好走的前N条路。这里的N也叫Beam Width。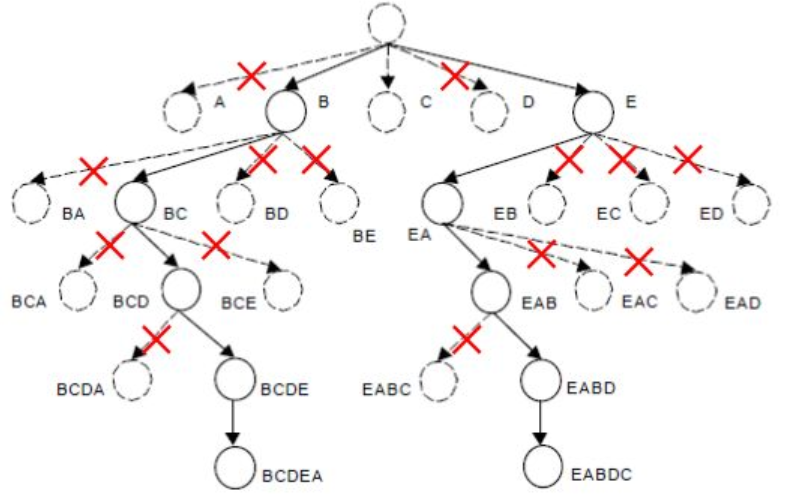
image.png

Viterbi算法

从后续计算中推导出前一步最优选择

  1. import decimal
  2. a = [[decimal.Decimal('0.5'), decimal.Decimal('0.4'), decimal.Decimal('0.1')],
  3.      [decimal.Decimal('0.2'), decimal.Decimal('0.2'), decimal.Decimal('0.6')],
  4.      [decimal.Decimal('0.2'), decimal.Decimal('0.5'), decimal.Decimal('0.3')]]
  6. b = [[decimal.Decimal('0.4'), decimal.Decimal('0.6')],
  7.      [decimal.Decimal('0.8'), decimal.Decimal('0.2')],
  8.      [decimal.Decimal('0.5'), decimal.Decimal('0.5')]]
  10. p = [decimal.Decimal('0.2'), decimal.Decimal('0.5'), decimal.Decimal('0.3')]
  12. white = 0
  13. black = 1
  15. status_list = [0, 1, 0, 0, 1]
  17. count = 1
  18. start = []
  19. for i in status_list:
  20.     if count == 1:
  21.         for b_son in range(len(b)):
  22.             start.append(p[b_son] * b[b_son][i])
  23.     else:
  24.         tmp_start = []
  25.         index = []
  26.         for a_son in range(len(a)):
  27.             tmp = []
  28.             for a_son_son in range(len(a[a_son])):
  29.                 # print(a[a_son_son][a_son], b[a_son][i], start[a_son_son])
  30.                 tmp.append(a[a_son_son][a_son] * b[a_son][i] * start[a_son_son])
  31.             tmp_max = max(tmp)
  32.             # print(tmp.index(tmp_max))
  33.             index.append(tmp.index(tmp_max))
  34.             tmp_start.append(tmp_max)
  35.         start = tmp_start
  36.         print(index)
  37.     last = i
  38.     count -= 1
  39.     print(start)