CRC算法

CRC算法将长度为m位的消息对应一个GF(2)多项式M，比如对于8位消息11100110，如果先传输
MSB，则它对应的多项式为x^7 + x^6 + x^5 + x^2 + x。
发送端和接收端约定一个次数为r的GF(2)多项式G，称为生成多项式，比如x^3 + x + 1，r = 3。
在消息后面加上r个0对应的多项式为M’，显然有M’ = Mx^r。用M’除以G将得到一个次数等于或小于r - 1的余数多项式R，
其对应的r位数值则为校验码。如下所示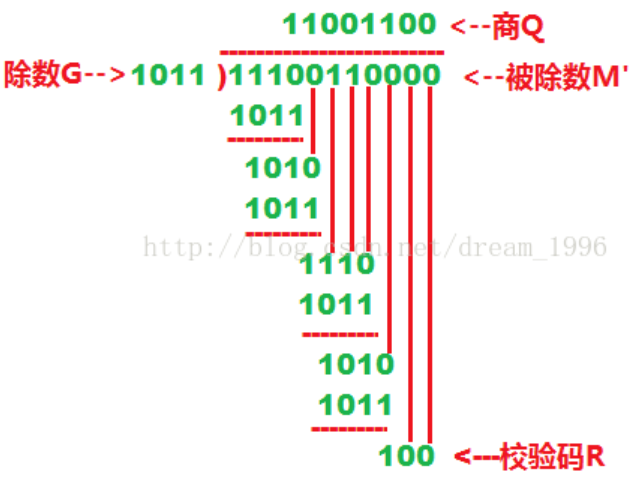

发送端将m位消息连同r位校验码(也就是M’ + R)一起发送出去，
接收端按同样的方法算出收到的m位消息的校验码，再与收到的校验码比较。
接收端也可以用收到的全部m + r位除以生成多项式，再判断余数是否为0。
这是因为，M’ + R = (QG + R) + R = QG，这里Q是商。
显然，它也可以像发送端一样，在全部m + r后再增加r个0，再除以生成多项式，
如果没有差错发生，余数仍然为0

不同的生成多项式，其检错能力是不同的。如何选择一个好的生成多项式需要一定
的数学理论，目前已经有很多多项式可供选择