三个盒子,编号为1,2,3;每个盒子都装有黑白两种颜色的小球,球的比例。如下:
| 编号 | 白球 | 黑球 |
|---|---|---|
| 1 | 4 | 6 |
| 2 | 8 | 2 |
| 3 | 5 | 5 |
模型λ=(A,B,π)
1、状态集合: S={盒子1,盒子2,盒子3}
2、观测集合: O={白,黑}
3、状态序列和观测序列的长度 T=5 (我抽了5次) 白黑白白黑
4、初始概率分布 π: 表示初次抽时,抽到1盒子的概率是0.2,抽到2盒子的概率是0.5,抽到3盒子的概率是0.3。
5、状态转移概率矩阵 A:
A[0][0] = 0.5 表示当前我抽到1盒子,下次还抽到1盒子的概率是0.5; A[0][1] = 0.4 表示当前我抽到1盒子,下次抽到2盒子的概率是0.4; A[1][0] = 0.2 表示当前我抽到2盒子,下次抽到1盒子的概率是0.2;
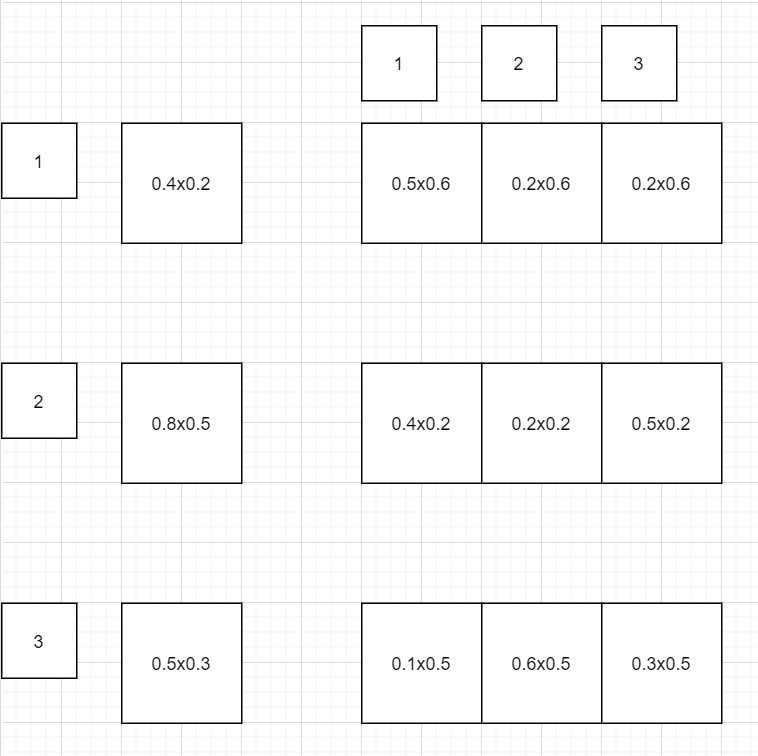
6、观测概率矩阵 - 混淆矩阵 - 为了不和之前的混淆矩阵概念冲突,可以称之为发射矩阵 B,即从一个状态发射到另一个状态: B:如最初的图,
b[0][0]=第一个盒子抽到白球概率0.4,b[0][1]=第一个盒子抽到黑球概率0.6;
维特比算法
import decimala = [[decimal.Decimal('0.5'), decimal.Decimal('0.4'), decimal.Decimal('0.1')],[decimal.Decimal('0.2'), decimal.Decimal('0.2'), decimal.Decimal('0.6')],[decimal.Decimal('0.2'), decimal.Decimal('0.5'), decimal.Decimal('0.3')]]b = [[decimal.Decimal('0.4'), decimal.Decimal('0.6')],[decimal.Decimal('0.8'), decimal.Decimal('0.2')],[decimal.Decimal('0.5'), decimal.Decimal('0.5')]]p = [decimal.Decimal('0.2'), decimal.Decimal('0.5'), decimal.Decimal('0.3')]white = 0black = 1status_list = [0, 1, 0, 0, 1]count = 1start = []for i in status_list:if count == 1:for b_son in range(len(b)):start.append(p[b_son] * b[b_son][i])else:tmp_start = []index = []for a_son in range(len(a)):tmp = []for a_son_son in range(len(a[a_son])):# print(a[a_son_son][a_son], b[a_son][i], start[a_son_son])tmp.append(a[a_son_son][a_son] * b[a_son][i] * start[a_son_son])tmp_max = max(tmp)# print(tmp.index(tmp_max))index.append(tmp.index(tmp_max))tmp_start.append(tmp_max)start = tmp_startprint(index)last = icount -= 1print(start)

