马尔可夫链

概述

马尔可夫链指的是一个状态空间中从一个状态转移到另一个状态的随机过程，在马尔可夫链中，某一时刻的状态的概率分布仅与其前一个状态有关，而与当前时刻之前的状态无关。从数学上来看则如下面的式子所示：

假设状态空间一共有n个状态，那么可以用一个n*n的矩阵完全表示整个状态空间中从一个状态转移到另一个状态的概率，这个矩阵的元素表示从状态转移到状态的概率，这矩阵称为状态转移矩阵。

状态转移矩阵的性质

状态转移矩阵根据定义有一个特点，对于任意的而言，。对于非周期的状态转移矩阵而言，它的n次幂最终会收敛到一个确定的值而不再发生变化。

import numpy as np
matrix = np.matrix([[0.8,0.075,0.125],[0.15,0.6,0.25],[0.25,0.15,0.6]])
def compute_n(matrix,n):
    p = matrix
    for i in range(n):
        p= p*matrix
        print("current round: ",i+1)
        print(p)
compute_n(matrix,45)

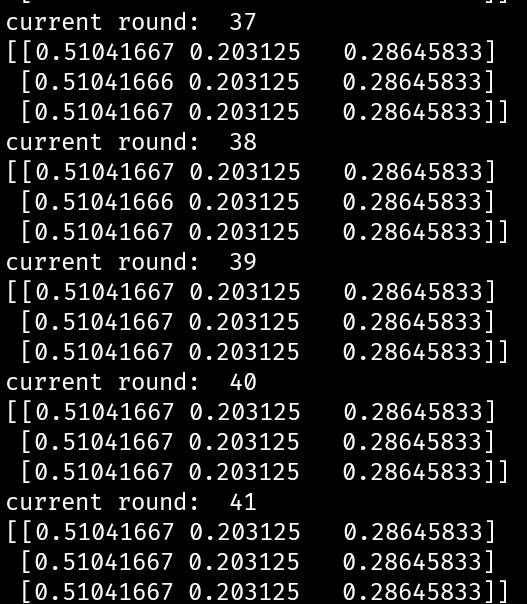
可以看到在第40轮，也就是P的41次方时，开始收敛了。其实应该在更早的时候就收敛，但是由于计算机的精度问题，导致其显示的收敛速度变慢。

• 状态转移矩阵的n次幂如果收敛，则给定j对于任意的i，都相同。

这个是非常好理解的，由于P的每一行加起来都为1，所以当使用矩阵乘法的时候，按照矩阵乘法的定义，只有满足此性质时，才会成立，也就是收敛。

有了上述的基础，我们可以用数学语言严谨地总结马尔可夫状态转移矩阵的性质了。

1. 如果一个马尔可夫链有非周期状态转移矩阵，并且其任何连个状态是连通的，则有
2. ,
3. 是的唯一非负解，通常称为马尔可夫链的平稳分布

4. 如果非周期马尔可夫链的状态转移矩阵P和概率分布对于所有的满足,则称是此马尔可夫链的平稳分布，此条件又称为马尔可夫链的细致平稳条件

   基于马尔可夫链的采样

   对于一个马尔可夫链，假设初始状态(的概率分布)为,已知其状态转移矩阵为，则经过次状态变化的状态(的概率分布)。当足够大，状态转移矩阵收敛时，也会收敛，且,且无论初始状态如何，马尔可夫链都会收敛到相同的状态，也就是达到了马尔可夫链的平稳分布，因此可以利用马尔可夫链的平稳分布性质进行采样。

   采样过程

   首先，从一个简单的概率分布中采样得到一个具体的值，由状态转移矩阵可以得到条件概率，是一个状态概率变量，例如[0.6,0.1,0.3]，接着使用均匀分布采样获得一个新的值，如此经过n次迭代之后得到最终采样值。基于上述说明，可以对基于马尔可夫链的采样进行总结，一共分为三步：

5. 设定状态空间，以及对应的简单概率分布。

6. 按照1中的概率分布进行采样得到1个初始样本
7. 对于2中采集得到的初始样本，设定待采样样本数N，基于马尔可夫链的状态转移矩阵进行n+N次迭代并采样，得到最终的N个样本，由马尔可夫链的性质可知，这N个样本符合马尔可夫链的平稳分布

   说明

   采样的基础是均匀分布采样，均匀分布采样的基础是均匀分布随机数的生成。
   在计算机中，无法产生真正意义上的随机数，只能生成伪随机数。产生均匀分布的伪随机数的一种常用方法是线性同余法（LCG），它利用一个递归式生成内的均匀分布的随机数，。假设需要产生一个[p,q]范围的均匀分布的随机数，只要做一个简单的映射令。
   已有均匀分布随机数生成器，那么就能轻易地实现一些简单的概率分布采样了。例如假设有一个离散随机变量，有三个不同的取值，其概率分布为[0.1,0.6,0.3]，采样方法为使用均匀分布随机数生成器生成一个[0,1]之间的随机数b，若,则取,若，则取，若，则取。

总结

上述内容说明了我们可以从任何简单的概率分布开始采样，通过马尔可夫链的变换，最终得到符合分布的样本。如果已知需要采样数据的概率分布，那么只需要找到这个分布对应的状态转移矩阵，因此利用马尔可夫链采样的问题就变成了已知平稳分布，如何求状态转移矩阵。只要能解决这个问题，那么就可以实现对任意概率分布的采样。马尔可夫链采样的主要优点是对于一些条件概率相对好求，但是其本身的概率不太好求的分布而言，可以更轻松地实现较高质量的采样。