RNN、GRU、LSTM与Transformer

RNN

设计RNN的动机是为了利用序列信息。在传统的神经网络中，每一层内的神经元是互相独立的，这种结构对于很多问题是无能为力的，比如下一个单词预测，语言翻译等序列问题。RNN的全称是Recurrent Neural Network（循环神经网络），之所以称为Recurrent是因为它对序列中的每一个元素都执行相同的操作。神经元的输出不仅仅和输入有关，还与之前的神经元状态有关。通常来讲，我们认为RNN具有记忆能力，并且从理论上来讲，RNN可以处理任意长度的序列，并记忆序列信息，但是实际操作中我们发现RNN只能处理有限长度的序列。RNN的结构以及运算方式如下：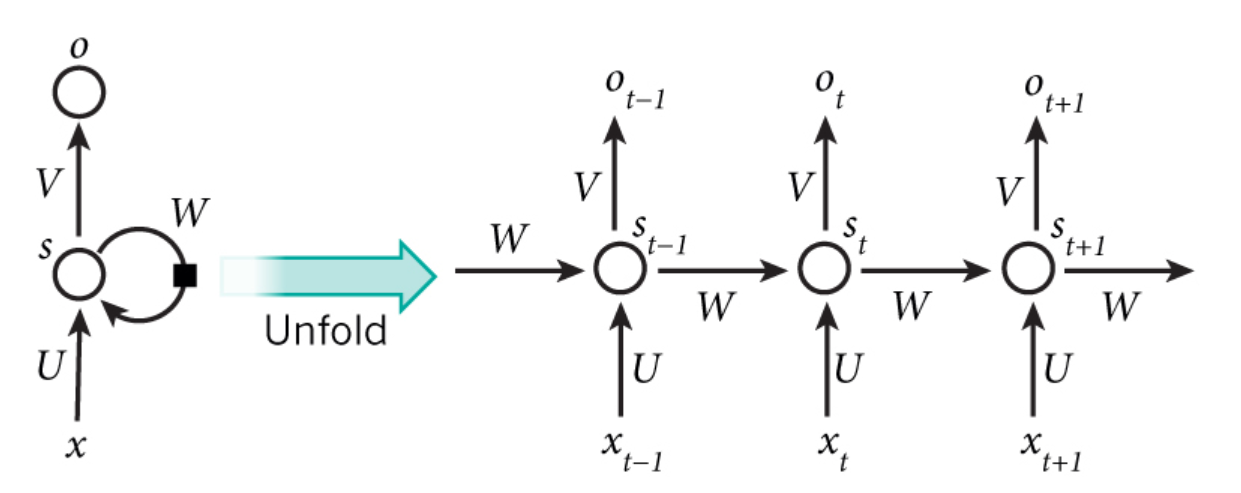


（隐藏状态）可以视作网络的记忆力，保存了之前计算的结果，也就是通过这种方式利用了序列信息。值得注意的是，在RNN中，对于序列的每一个输入，都是一样的，反映了Recurrent这个词的含义。并不是每一个输入都需要一个输出，对于不同的任务，需要的输出不同，RNN的核心是隐藏状态，也即序列的特征，就像CNN一样，输出根据需要变化。

RNN能做什么

RNN主要用于NLP中，因为语言是非常明显的序列信息。常见的任务有语言建模、文本生成、机器翻译、语音识别、图像描述生成 。

RNN的训练

RNN也像其他的神经网络一样使用梯度反向传播进行训练，但是有一点小小的不同值得注意。我们知道RNN的权重参数是共享的，那么也就意味着为了计算当前步的梯度，需要同时计算之前步骤的梯度并求和，这种方式称为Backpropagation through time(BPTT)。

BPTT

RNN反向传播.pdf
https://github.com/go2carter/nn-learn/blob/master/grad-deriv-tex/rnn-grad-deriv.pdf
执行代码：

def bptt(self, x, y):
    T = len(y)
    # Perform forward propagation
    o, s = self.forward_propagation(x)
    # We accumulate the gradients in these variables
    dLdU = np.zeros(self.U.shape)
    dLdV = np.zeros(self.V.shape)
    dLdW = np.zeros(self.W.shape)
    delta_o = o
    delta_o[np.arange(len(y)), y] -= 1.
    # For each output backwards...
    for t in np.arange(T)[::-1]:
        dLdV += np.outer(delta_o[t], s[t].T)
        # Initial delta calculation: dL/dz
        delta_t = self.V.T.dot(delta_o[t]) * (1 - (s[t] ** 2))
        #1-s[t]**2 means the derivative of activate function tanh
        # Backpropagation through time (for at most self.bptt_truncate steps)
        for bptt_step in np.arange(max(0, t-self.bptt_truncate), t+1)[::-1]:
            # print "Backpropagation step t=%d bptt step=%d " % (t, bptt_step)
            # Add to gradients at each previous step
            dLdW += np.outer(delta_t, s[bptt_step-1])              
            dLdU[:,x[bptt_step]] += delta_t
            # Update delta for next step dL/dz at t-1
            delta_t = self.W.T.dot(delta_t) * (1 - s[bptt_step-1] ** 2)
            #self.W = ds[t]/ds[t-1]
    return [dLdU, dLdV, dLdW]

RNN的缺陷

由上面的RNN的训练过程可以看到，和CNN一样，由于权重连乘的存在，一旦序列过长，会发生梯度爆照或者梯度消失，也即RNN不能捕捉长时依赖，为了改善RNN的这个问题，就有了LSTM和GRU。

LSTM

STM的核心思想是增加了一个单元状态（cell state)，这个状态可以记忆信息。为了计算这个单元状态，LSTM使用了门（gate）的的结构，这个结构让LSTM具有了往cell中移除或者增加信息的能力。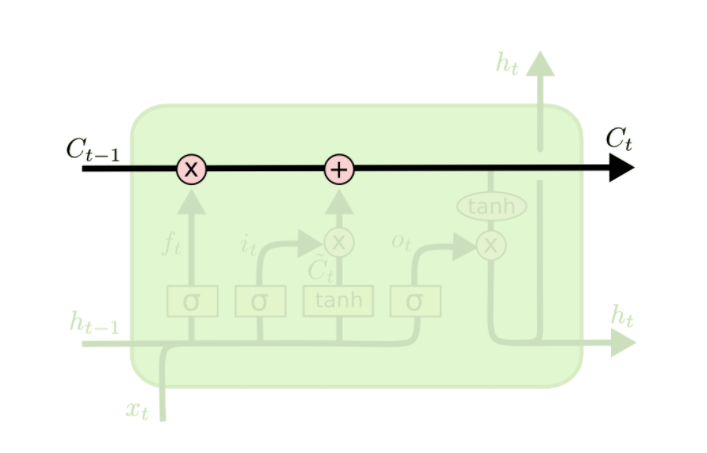

一种可以记忆长时信息的RNN变种，它和RNN有一样的结构，区别就是改进了隐藏层（state）的计算方式。下面两幅图可以比较RNN和LSTM的区别。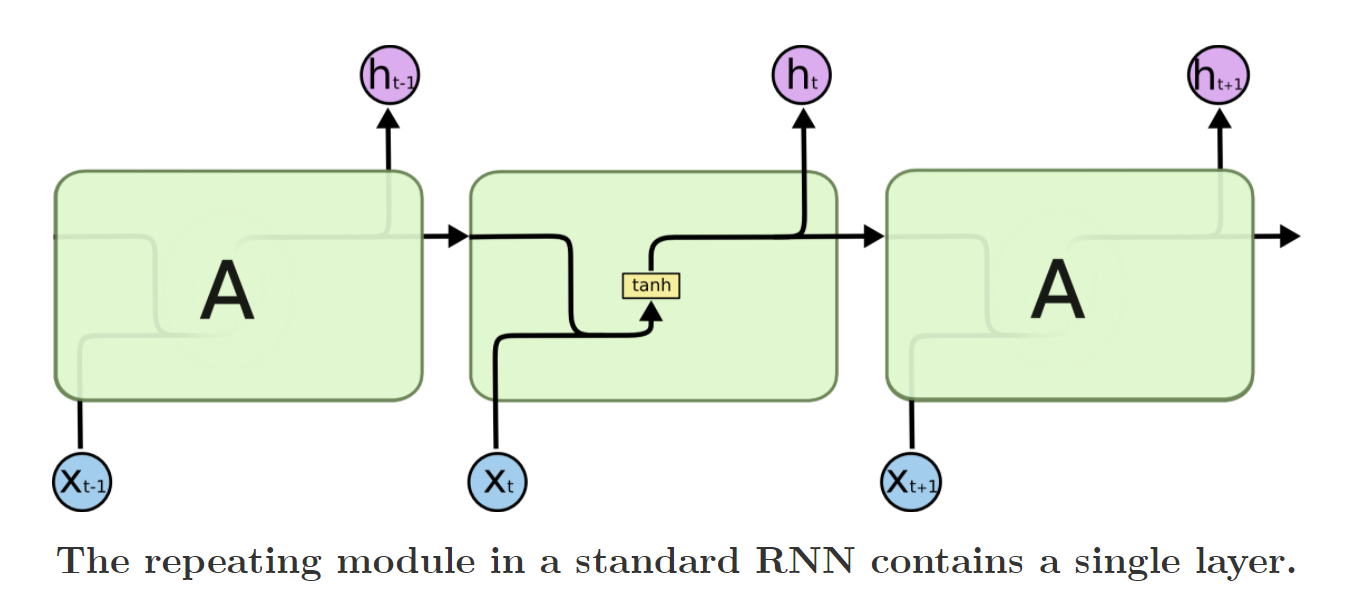

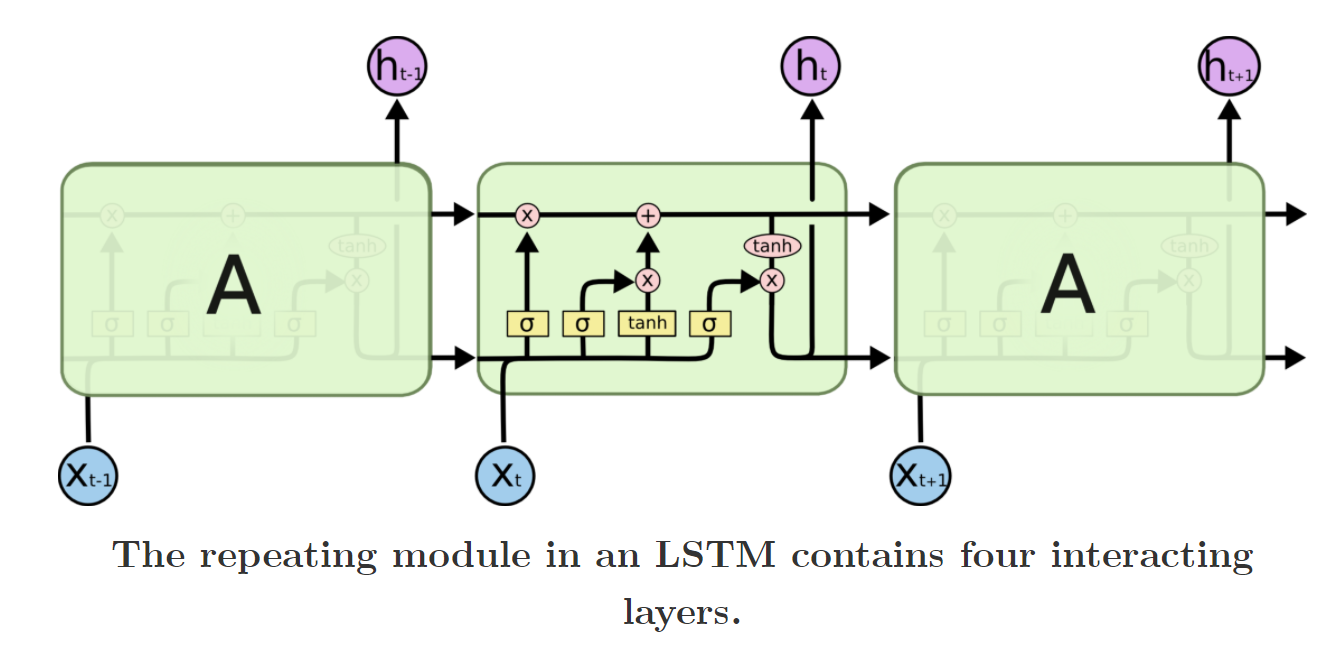
我们看看LSTM一个单元内部是如何交互的：

是遗忘门，意味着要记忆多少的内容，即部分。LSTM还可以决定往中增加多少内容，即部分。门的概念即得到一系列的系数。

GRU

GRU是LSTM的一个变种，它将遗忘门和输入门合并为一个更新门，并且也将cell state和hidden state合并，并做了一些其他改进。经过这些改动，模型变得更加简单，GRU单元的图如下：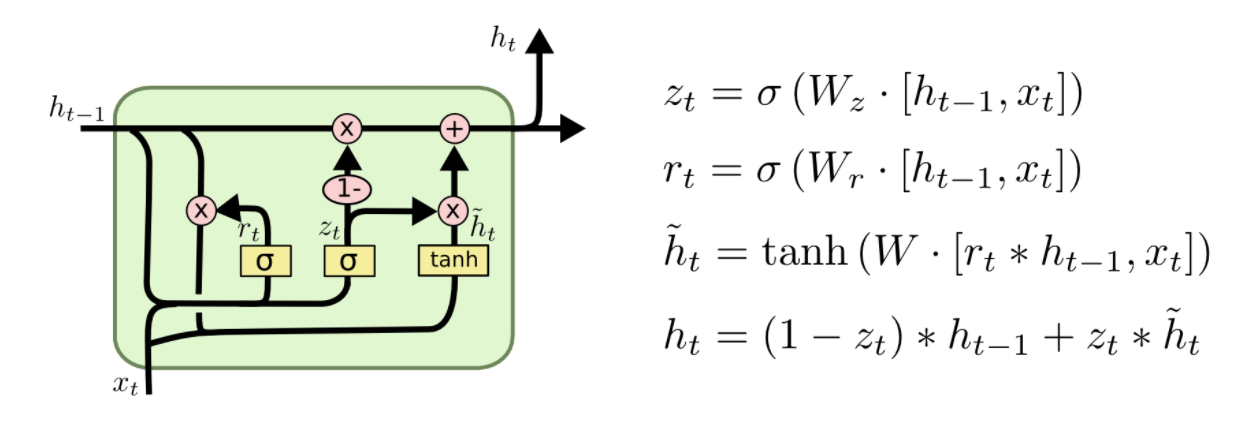

，输出门和候选输入的作用用取代。

Transformer

用记忆力捕捉序列之间元素的关系，可以捕捉任意长度的关系，不存在梯度消失和梯度爆炸的问题。多个注意力层构成了Transformer模型。